Orden de permutación: para una permutación dada P si P n = I (permutación de identidad), entonces n es el orden de permutación.
Sea una permutación 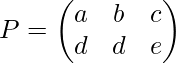
y P n = yo = 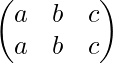
Entonces n es el orden de permutación.
Ejemplo 1-: Cuantas veces 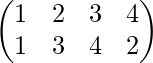 se multiplica a si mismo para producir
se multiplica a si mismo para producir 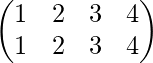
Solución-: Sea P=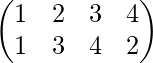
Entonces P 2 =PP=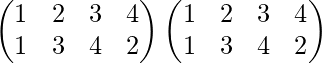
PAG 2 =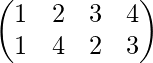
PAG 3 = PAG 2 .P=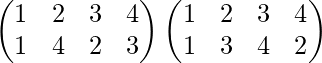
P 3 =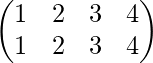 = yo
= yo
Por lo tanto, el número requerido es 3.
orden=3
Ejemplo 2-: Encuentra el orden de permutación ![]() .
.
Solución-: Sea la permutación dada P= ![]()
Podemos escribir P como P= 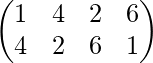
PAG 2 =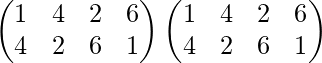
=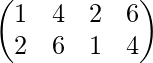
P 3 =P 2 .P=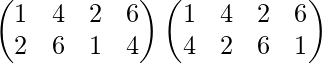
=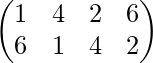
P 4 =P 3 .P=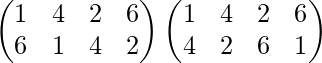
=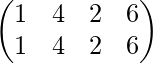
P 4 =I (permutación de identidad)
Por lo tanto, el orden es 4.
Publicación traducida automáticamente
Artículo escrito por portalpirate y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA