Dado un árbol binario, imprima el recorrido del orden de niveles de manera que los Nodes de todos los niveles se impriman en líneas separadas.
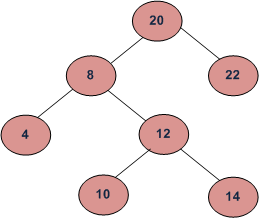
Por ejemplo, considere el siguiente árbol
Example 1:
C++
/* Function to line by line print level order traversal a tree*/
void printLevelOrder(struct node* root)
{
int h = height(root);
int i;
for (i=1; i<=h; i++)
{
printGivenLevel(root, i);
printf("\n");
}
}
/* Print nodes at a given level */
void printGivenLevel(struct node* root, int level)
{
if (root == NULL)
return;
if (level == 1)
printf("%d ", root->data);
else if (level > 1)
{
printGivenLevel(root->left, level-1);
printGivenLevel(root->right, level-1);
}
}
Java
/* Function to line by line print level order traversal a tree*/
static void printLevelOrder(Node root)
{
int h = height(root);
int i;
for (i=1; i<=h; i++)
{
printGivenLevel(root, i);
System.out.println();
}
}
/* Print nodes at a given level */
void printGivenLevel(Node root, int level)
{
if (root == null)
return;
if (level == 1)
System.out.println(root.data);
else if (level > 1)
{
printGivenLevel(root.left, level-1);
printGivenLevel(root.right, level-1);
}
}
Python3
# Python3 program for above approach def printlevelorder(root): h = height(root) for i in range(1, h + 1): givenspirallevel(root, i) def printGivenLevel(root, level): if root is None: return root if level == 1: print(root.val, end = ' ') elif level > 1: printGivenLevel(root.left, level - 1) printGivenLevel(root.right, level - 1) # This code is contributed by Praveen kumar
C#
/* Print nodes at a given level */
static void printGivenLevel(Node root, int level)
{
if (root == null)
return;
if (level == 1)
Console.WriteLine(root.data);
else if (level > 1)
{
printGivenLevel(root.left, level-1);
printGivenLevel(root.right, level-1);
}
}
Javascript
/* Print nodes at a given level */
function printGivenLevel(root, level)
{
if (root == null)
return;
if (level == 1)
document.write(root.data);
else if (level > 1)
{
printGivenLevel(root.left, level-1);
printGivenLevel(root.right, level-1);
}
}
C++
/* Iterative program to print levels line by line */
#include <iostream>
#include <queue>
using namespace std;
// A Binary Tree Node
struct node
{
struct node *left;
int data;
struct node *right;
};
// Iterative method to do level order traversal
// line by line
void printLevelOrder(node *root)
{
// Base Case
if (root == NULL) return;
// Create an empty queue for level order traversal
queue<node *> q;
// Enqueue Root and initialize height
q.push(root);
while (q.empty() == false)
{
// nodeCount (queue size) indicates number
// of nodes at current level.
int nodeCount = q.size();
// Dequeue all nodes of current level and
// Enqueue all nodes of next level
while (nodeCount > 0)
{
node *node = q.front();
cout << node->data << " ";
q.pop();
if (node->left != NULL)
q.push(node->left);
if (node->right != NULL)
q.push(node->right);
nodeCount--;
}
cout << endl;
}
}
// Utility function to create a new tree node
node* newNode(int data)
{
node *temp = new node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
// Driver program to test above functions
int main()
{
// Let us create binary tree shown above
node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->right = newNode(6);
printLevelOrder(root);
return 0;
}
Java
/* An Iterative Java program to print levels line by line */
import java.util.LinkedList;
import java.util.Queue;
public class LevelOrder
{
// A Binary Tree Node
static class Node
{
int data;
Node left;
Node right;
// constructor
Node(int data){
this.data = data;
left = null;
right =null;
}
}
// Iterative method to do level order traversal line by line
static void printLevelOrder(Node root)
{
// Base Case
if(root == null)
return;
// Create an empty queue for level order traversal
Queue<Node> q =new LinkedList<Node>();
// Enqueue Root and initialize height
q.add(root);
while(true)
{
// nodeCount (queue size) indicates number of nodes
// at current level.
int nodeCount = q.size();
if(nodeCount == 0)
break;
// Dequeue all nodes of current level and Enqueue all
// nodes of next level
while(nodeCount > 0)
{
Node node = q.peek();
System.out.print(node.data + " ");
q.remove();
if(node.left != null)
q.add(node.left);
if(node.right != null)
q.add(node.right);
nodeCount--;
}
System.out.println();
}
}
// Driver program to test above functions
public static void main(String[] args)
{
// Let us create binary tree shown in above diagram
/* 1
/ \
2 3
/ \ \
4 5 6
*/
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
printLevelOrder(root);
}
}
//This code is contributed by Sumit Ghosh
Python3
# Python3 program for above approach
class newNode:
def __init__(self, data):
self.val = data
self.left = None
self.right = None
# Iterative method to do level order traversal
# line by line
def printLevelOrder(root):
# Base case
if root is None:
return
# Create an empty queue for level order traversal
q = []
# Enqueue root and initialize height
q.append(root)
while q:
# nodeCount (queue size) indicates number
# of nodes at current level.
count = len(q)
# Dequeue all nodes of current level and
# Enqueue all nodes of next level
while count > 0:
temp = q.pop(0)
print(temp.val, end = ' ')
if temp.left:
q.append(temp.left)
if temp.right:
q.append(temp.right)
count -= 1
print(' ')
# Driver Code
root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.right = newNode(6);
printLevelOrder(root);
# This code is contributed by Praveen kumar
C#
/* An Iterative C# program to print
levels line by line */
using System;
using System.Collections.Generic;
public class LevelOrder
{
// A Binary Tree Node
class Node
{
public int data;
public Node left;
public Node right;
// constructor
public Node(int data)
{
this.data = data;
left = null;
right =null;
}
}
// Iterative method to do level order
// traversal line by line
static void printLevelOrder(Node root)
{
// Base Case
if(root == null)
return;
// Create an empty queue for level
// order traversal
Queue<Node> q =new Queue<Node>();
// Enqueue Root and initialize height
q.Enqueue(root);
while(true)
{
// nodeCount (queue size) indicates
// number of nodes at current level.
int nodeCount = q.Count;
if(nodeCount == 0)
break;
// Dequeue all nodes of current level
// and Enqueue all nodes of next level
while(nodeCount > 0)
{
Node node = q.Peek();
Console.Write(node.data + " ");
q.Dequeue();
if(node.left != null)
q.Enqueue(node.left);
if(node.right != null)
q.Enqueue(node.right);
nodeCount--;
}
Console.WriteLine();
}
}
// Driver Code
public static void Main(String[] args)
{
// Let us create binary tree shown
// in above diagram
/* 1
/ \
2 3
/ \ \
4 5 6
*/
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
printLevelOrder(root);
}
}
// This code is contributed 29AjayKumar
Javascript
<script>
/* An Iterative Javascript program to
print levels line by line */
class Node
{
constructor(data) {
this.left = null;
this.right = null;
this.data = data;
}
}
// Iterative method to do level order traversal line by line
function printLevelOrder(root)
{
// Base Case
if(root == null)
return;
// Create an empty queue for level order traversal
let q = [];
// Enqueue Root and initialize height
q.push(root);
while(true)
{
// nodeCount (queue size) indicates number of nodes
// at current level.
let nodeCount = q.length;
if(nodeCount == 0)
break;
// Dequeue all nodes of current level and Enqueue all
// nodes of next level
while(nodeCount > 0)
{
let node = q[0];
document.write(node.data + " ");
q.shift();
if(node.left != null)
q.push(node.left);
if(node.right != null)
q.push(node.right);
nodeCount--;
}
document.write("</br>");
}
}
// Let us create binary tree shown in above diagram
/* 1
/ \
2 3
/ \ \
4 5 6
*/
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
printLevelOrder(root);
</script>
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA