El límite inferior para el algoritmo de clasificación basado en Comparación (Merge Sort, Heap Sort, Quick-Sort… etc.) es Ω(nLogn), es decir, no pueden hacerlo mejor que nLogn . La ordenación por conteo es un algoritmo de ordenación de tiempo lineal que ordena en tiempo O(n+k) cuando los elementos están en el rango de 1 a k.
¿Qué pasa si los elementos están en el rango de 1 a n 2 ?
No podemos usar la ordenación por conteo porque la ordenación por conteo tomará O(n 2 ), que es peor que los algoritmos de ordenación basados en comparación. ¿Podemos ordenar tal array en tiempo lineal?
Radix Sort es la respuesta. La idea de Radix Sort es ordenar dígito por dígito comenzando desde el dígito menos significativo hasta el dígito más significativo. Radix sort usa la ordenación por conteo como una subrutina para ordenar.
El algoritmo de clasificación Radix
Haga lo siguiente para cada dígito i donde i varía del dígito menos significativo al dígito más significativo. Aquí estaremos ordenando la array de entrada utilizando la ordenación por conteo (o cualquier ordenación estable) de acuerdo con el i-ésimo dígito.
Ejemplo:
Lista original sin clasificar: 170, 45, 75, 90, 802, 24, 2, 66 Ordenar por el dígito menos significativo (1) da: [*Observe que mantenemos 802 antes que 2, porque 802 apareció antes que 2 en la lista original , y de manera similar para los pares 170 y 90 y 45 y 75.] 17 0 , 9 0 , 80 2 , 2 , 2 4 , 4 5 , 7 5 , 6 6 Ordenar por el siguiente dígito (lugar de las decenas) da: [*Observe que 802 nuevamente viene antes que 2 como 802 viene antes que 2 en la lista anterior.] 8 0 2, 2, 2 4, 4 5, 6 6, 1 7 0, 7 5, 90 Ordenar por el dígito más significativo (centésimas) da: 2, 24, 45, 66, 75, 90, 1 70, 8 02
¿Cuál es el tiempo de funcionamiento de Radix Sort?
Deje que haya d dígitos en los enteros de entrada. Radix Sort toma tiempo O(d*(n+b)) donde b es la base para representar números, por ejemplo, para el sistema decimal, b es 10. ¿Cuál es el valor de d? Si k es el valor máximo posible, entonces d sería O(log b (k)). Entonces, la complejidad del tiempo total es O((n+b) * log b (k)). Lo que parece más que la complejidad temporal de los algoritmos de clasificación basados en comparación para una k grande. Primero limitemos k. Sea k <= n c donde c es una constante. En ese caso, la complejidad se convierte en O(nLog b (n)). Pero todavía no supera los algoritmos de clasificación basados en la comparación.
¿Y si hacemos más grande el valor de b?. ¿Cuál debería ser el valor de b para que la complejidad del tiempo sea lineal? Si establecemos b como n, obtenemos la complejidad temporal como O(n). En otras palabras, podemos ordenar una array de enteros con un rango de 1 a n c si los números se representan en base n (o cada dígito toma log 2 (n) bits).
Aplicaciones de Radix Sort:
- En una computadora típica, que es una máquina secuencial de acceso aleatorio, donde los registros están codificados por múltiples campos, se usa la ordenación radix. Por ejemplo, desea ordenar en tres claves mes, día y año. Puede comparar dos registros en el año, luego en un empate en el mes y finalmente en la fecha. Alternativamente, podría usarse ordenar los datos tres veces usando Radix sort primero en la fecha, luego en el mes y finalmente en el año.
- Se usó en máquinas clasificadoras de tarjetas que tenían 80 columnas, y en cada columna, la máquina podía perforar un agujero solo en 12 lugares. Luego, el clasificador se programó para clasificar las tarjetas, según el lugar en el que se había perforado la tarjeta. Luego, el operador lo utilizó para recoger las tarjetas que tenían la primera fila perforada, seguida de la segunda fila, y así sucesivamente.
¿Es Radix Sort preferible a los algoritmos de clasificación basados en comparación como Quick-Sort?
Si tenemos log 2 n bits para cada dígito, el tiempo de ejecución de Radix parece ser mejor que Quick Sort para una amplia gama de números de entrada. Los factores constantes ocultos en la notación asintótica son más altos para Radix Sort y Quick-Sort usa cachés de hardware de manera más efectiva. Además, la ordenación Radix utiliza la ordenación por conteo como una subrutina y la ordenación por conteo ocupa espacio adicional para ordenar números.
Puntos clave sobre Radix Sort:
Aquí se dan algunos puntos clave sobre la ordenación radix.
- Hace suposiciones sobre los datos como si los datos deben estar entre un rango de elementos.
- La array de entrada debe tener los elementos con la misma raíz y ancho.
- Radix sort funciona en la clasificación basada en dígitos individuales o posición de letras.
- Debemos comenzar a ordenar desde la posición más a la derecha y usar un algoritmo estable en cada posición.
- Radix sort no es un algoritmo en el lugar, ya que utiliza una array de conteo temporal.
diagramas de flujo
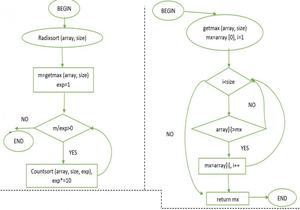
Clasificación radix del diagrama de flujo, getmax
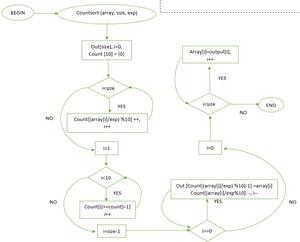
Conteo de diagrama de flujo
Implementación: Radix Sort
A continuación se muestra una implementación simple de Radix Sort. Para simplificar, se supone que el valor de d es 10. Le recomendamos que consulte Ordenar por conteo para obtener detalles de la función contarSort() en el siguiente código.
C++
// C++ implementation of Radix Sort
#include <iostream>
using namespace std;
// A utility function to get maximum value in arr[]
int getMax(int arr[], int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// A function to do counting sort of arr[] according to
// the digit represented by exp.
void countSort(int arr[], int n, int exp)
{
int output[n]; // output array
int i, count[10] = { 0 };
// Store count of occurrences in count[]
for (i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
// Change count[i] so that count[i] now contains actual
// position of this digit in output[]
for (i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for (i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[], so that arr[] now
// contains sorted numbers according to current digit
for (i = 0; i < n; i++)
arr[i] = output[i];
}
// The main function to that sorts arr[] of size n using
// Radix Sort
void radixsort(int arr[], int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// Do counting sort for every digit. Note that instead
// of passing digit number, exp is passed. exp is 10^i
// where i is current digit number
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}
// A utility function to print an array
void print(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}
// Driver Code
int main()
{
int arr[] = { 170, 45, 75, 90, 802, 24, 2, 66 };
int n = sizeof(arr) / sizeof(arr[0]);
// Function Call
radixsort(arr, n);
print(arr, n);
return 0;
}
Java
// Radix sort Java implementation
import java.io.*;
import java.util.*;
class Radix {
// A utility function to get maximum value in arr[]
static int getMax(int arr[], int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// A function to do counting sort of arr[] according to
// the digit represented by exp.
static void countSort(int arr[], int n, int exp)
{
int output[] = new int[n]; // output array
int i;
int count[] = new int[10];
Arrays.fill(count, 0);
// Store count of occurrences in count[]
for (i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
// Change count[i] so that count[i] now contains
// actual position of this digit in output[]
for (i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for (i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[], so that arr[] now
// contains sorted numbers according to current
// digit
for (i = 0; i < n; i++)
arr[i] = output[i];
}
// The main function to that sorts arr[] of
// size n using Radix Sort
static void radixsort(int arr[], int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// Do counting sort for every digit. Note that
// instead of passing digit number, exp is passed.
// exp is 10^i where i is current digit number
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}
// A utility function to print an array
static void print(int arr[], int n)
{
for (int i = 0; i < n; i++)
System.out.print(arr[i] + " ");
}
// Main driver method
public static void main(String[] args)
{
int arr[] = { 170, 45, 75, 90, 802, 24, 2, 66 };
int n = arr.length;
// Function Call
radixsort(arr, n);
print(arr, n);
}
}
Python3
# Python program for implementation of Radix Sort # A function to do counting sort of arr[] according to # the digit represented by exp. def countingSort(arr, exp1): n = len(arr) # The output array elements that will have sorted arr output = [0] * (n) # initialize count array as 0 count = [0] * (10) # Store count of occurrences in count[] for i in range(0, n): index = arr[i] // exp1 count[index % 10] += 1 # Change count[i] so that count[i] now contains actual # position of this digit in output array for i in range(1, 10): count[i] += count[i - 1] # Build the output array i = n - 1 while i >= 0: index = arr[i] // exp1 output[count[index % 10] - 1] = arr[i] count[index % 10] -= 1 i -= 1 # Copying the output array to arr[], # so that arr now contains sorted numbers i = 0 for i in range(0, len(arr)): arr[i] = output[i] # Method to do Radix Sort def radixSort(arr): # Find the maximum number to know number of digits max1 = max(arr) # Do counting sort for every digit. Note that instead # of passing digit number, exp is passed. exp is 10^i # where i is current digit number exp = 1 while max1 / exp > 1: countingSort(arr, exp) exp *= 10 # Driver code arr = [170, 45, 75, 90, 802, 24, 2, 66] # Function Call radixSort(arr) for i in range(len(arr)): print(arr[i],end=" ") # This code is contributed by Mohit Kumra # Edited by Patrick Gallagher
C#
// C# implementation of Radix Sort
using System;
class GFG {
public static int getMax(int[] arr, int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// A function to do counting sort of arr[] according to
// the digit represented by exp.
public static void countSort(int[] arr, int n, int exp)
{
int[] output = new int[n]; // output array
int i;
int[] count = new int[10];
// initializing all elements of count to 0
for (i = 0; i < 10; i++)
count[i] = 0;
// Store count of occurrences in count[]
for (i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
// Change count[i] so that count[i] now contains
// actual
// position of this digit in output[]
for (i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for (i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[], so that arr[] now
// contains sorted numbers according to current
// digit
for (i = 0; i < n; i++)
arr[i] = output[i];
}
// The main function to that sorts arr[] of size n using
// Radix Sort
public static void radixsort(int[] arr, int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// Do counting sort for every digit. Note that
// instead of passing digit number, exp is passed.
// exp is 10^i where i is current digit number
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}
// A utility function to print an array
public static void print(int[] arr, int n)
{
for (int i = 0; i < n; i++)
Console.Write(arr[i] + " ");
}
// Driver Code
public static void Main()
{
int[] arr = { 170, 45, 75, 90, 802, 24, 2, 66 };
int n = arr.Length;
// Function Call
radixsort(arr, n);
print(arr, n);
}
// This code is contributed by DrRoot_
}
PHP
<?php
// PHP implementation of Radix Sort
// A function to do counting sort of arr[]
// according to the digit represented by exp.
function countSort(&$arr, $n, $exp)
{
$output = array_fill(0, $n, 0); // output array
$count = array_fill(0, 10, 0);
// Store count of occurrences in count[]
for ($i = 0; $i < $n; $i++)
$count[ ($arr[$i] / $exp) % 10 ]++;
// Change count[i] so that count[i]
// now contains actual position of
// this digit in output[]
for ($i = 1; $i < 10; $i++)
$count[$i] += $count[$i - 1];
// Build the output array
for ($i = $n - 1; $i >= 0; $i--)
{
$output[$count[ ($arr[$i] /
$exp) % 10 ] - 1] = $arr[$i];
$count[ ($arr[$i] / $exp) % 10 ]--;
}
// Copy the output array to arr[], so
// that arr[] now contains sorted numbers
// according to current digit
for ($i = 0; $i < $n; $i++)
$arr[$i] = $output[$i];
}
// The main function to that sorts arr[]
// of size n using Radix Sort
function radixsort(&$arr, $n)
{
// Find the maximum number to know
// number of digits
$m = max($arr);
// Do counting sort for every digit. Note
// that instead of passing digit number,
// exp is passed. exp is 10^i where i is
// current digit number
for ($exp = 1; $m / $exp > 0; $exp *= 10)
countSort($arr, $n, $exp);
}
// A utility function to print an array
function PrintArray(&$arr,$n)
{
for ($i = 0; $i < $n; $i++)
echo $arr[$i] . " ";
}
// Driver Code
$arr = array(170, 45, 75, 90, 802, 24, 2, 66);
$n = count($arr);
// Function Call
radixsort($arr, $n);
PrintArray($arr, $n);
// This code is contributed by rathbhupendra
?>
Javascript
<script>
// Radix sort Javascript implementation
// A utility function to get maximum value in arr[]
function getMax(arr,n)
{
let mx = arr[0];
for (let i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// A function to do counting sort of arr[] according to
// the digit represented by exp.
function countSort(arr,n,exp)
{
let output = new Array(n); // output array
let i;
let count = new Array(10);
for(let i=0;i<10;i++)
count[i]=0;
// Store count of occurrences in count[]
for (i = 0; i < n; i++)
count[Math.floor(arr[i] / exp) % 10]++;
// Change count[i] so that count[i] now contains
// actual position of this digit in output[]
for (i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for (i = n - 1; i >= 0; i--) {
output[count[Math.floor(arr[i] / exp) % 10] - 1] = arr[i];
count[Math.floor(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[], so that arr[] now
// contains sorted numbers according to current digit
for (i = 0; i < n; i++)
arr[i] = output[i];
}
// The main function to that sorts arr[] of size n using
// Radix Sort
function radixsort(arr,n)
{
// Find the maximum number to know number of digits
let m = getMax(arr, n);
// Do counting sort for every digit. Note that
// instead of passing digit number, exp is passed.
// exp is 10^i where i is current digit number
for (let exp = 1; Math.floor(m / exp) > 0; exp *= 10)
countSort(arr, n, exp);
}
// A utility function to print an array
function print(arr,n)
{
for (let i = 0; i < n; i++)
document.write(arr[i] + " ");
}
/*Driver Code*/
let arr=[170, 45, 75, 90, 802, 24, 2, 66];
let n = arr.length;
// Function Call
radixsort(arr, n);
print(arr, n);
// This code is contributed by rag2127
</script>
2 24 45 66 75 90 170 802
La siguiente es otra forma de implementar la ordenación radix mientras se usa la técnica de ordenación de cubeta, puede que no parezca simple al mirar el código, pero si lo intenta, es bastante fácil, uno debe conocer la ordenación de cubeta a mayor profundidad .
C++
// implementation of radix sort using bin/bucket sort
#include <bits/stdc++.h>
using namespace std;
// structure for a single linked list to help further in the
// sorting
struct node {
int data;
node* next;
};
// function for creating a new node in the linked list
struct node* create(int x)
{
node* temp = new node();
temp->data = x;
temp->next = NULL;
return temp;
}
// utility function to append node in the linked list
// here head is passed by reference, to know more about this
// search pass by reference
void insert(node*& head, int n)
{
if (head == NULL) {
head = create(n);
return;
}
node* t = head;
while (t->next != NULL)
t = t->next;
t->next = create(n);
}
// utility function to pop an element from front in the list
// for the sake of stability in sorting
int del(node*& head)
{
if (head == NULL)
return 0;
node* temp = head;
// storing the value of head before updating
int val = head->data;
// updation of head to next node
head = head->next;
delete temp;
return val;
}
// utility function to get the number of digits in the
// max_element
int digits(int n)
{
int i = 1;
if (n < 10)
return 1;
while (n > (int)pow(10, i))
i++;
return i;
}
void radix_sort(vector<int>& arr)
{
// size of the array to be sorted
int sz = arr.size();
// getting the maximum element in the array
int max_val = *max_element(arr.begin(), arr.end());
// getting digits in the maximum element
int d = digits(max_val);
// creating buckets to store the pointers
node** bins;
// array of pointers to linked list of size 10 as
// integers are decimal numbers so they can hold numbers
// from 0-9 only, that's why size of 10
bins = new node*[10];
// initializing the hash array with null to all
for (int i = 0; i < 10; i++)
bins[i] = NULL;
// first loop working for a constant time only and inner
// loop is iterating through the array to store elements
// of array in the linked list by their digits value
for (int i = 0; i < d; i++) {
for (int j = 0; j < sz; j++) // bins updation
insert(bins[(arr[j] / (int)pow(10, i)) % 10],
arr[j]);
int x = 0, y = 0;
// write back to the array after each pass
while (x < 10) {
while (bins[x] != NULL)
arr[y++] = del(bins[x]);
x++;
}
}
}
// a utility function to print the sorted array
void print(vector<int> arr)
{
for (int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
cout << endl;
}
int main()
{
vector<int> arr = { 573, 25, 415, 12, 161, 6 };
// function call
radix_sort(arr);
print(arr);
return 0;
}
6 12 25 161 415 573
Las complejidades de tiempo siguen siendo las mismas que en el primer método, es solo la implementación a través de otro método.
Radix Sort on Strings: Radix sort se usa principalmente para ordenar los valores numéricos o los valores reales, pero se puede modificar para ordenar los valores de string en orden lexicográfico. Sigue el mismo procedimiento que se utiliza para los valores numéricos.
Consulte este enlace IDE para la implementación del mismo.
Input:[BCDEF, dbaqc, abcde, bbbbb] Output:[abcde, bbbbb, BCDEF, dbaqc]
Instantáneas:





Cuestionario sobre Radix Sort
Echa un vistazo al curso de autoaprendizaje de DSA
Otros algoritmos de clasificación en GeeksforGeeks/GeeksQuiz:
- Clasificación de selección
- Ordenamiento de burbuja
- Tipo de inserción
- Ordenar por fusión
- Ordenar montón
- Ordenación rápida
- Clasificación de conteo
- Clasificación de cubo
- ShellOrdenar
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA