Dada una array arr[] que consta de N enteros, la tarea es ordenar la array dada en orden ascendente utilizando la ordenación lenta.
Ejemplos:
Entrada: arr[] = {6, 8, 9, 4, 12, 1}
Salida: 1 4 6 8 9 12Entrada: arr[] = {5, 4, 3, 2, 1}
Salida: 1 2 3 4 5
Fusionar Ordenar Divide y vencerás Siga los pasos a continuación para resolver el problema:
Clasificación Lenta(arr[], l, r):
- Si r >= l , realice los siguientes pasos:
- Encuentre el valor medio de la array como m = (l + r) / 2 .
- Llame recursivamente a la función SlowSort para encontrar el máximo de los elementos de la primera mitad: SlowSort(arr, l, m)
- Llame recursivamente a la función SlowSort para encontrar el máximo de elementos de la segunda mitad: SlowSort(arr, m + 1, r)
- Almacene el mayor de los dos máximos devueltos por las llamadas a funciones anteriores al final como arr[r] = max(arr[m], arr[r])
- Llame recursivamente a la función SlowSort sin el máximo obtenido en el paso anterior: SlowSort(arr, l, r-1)
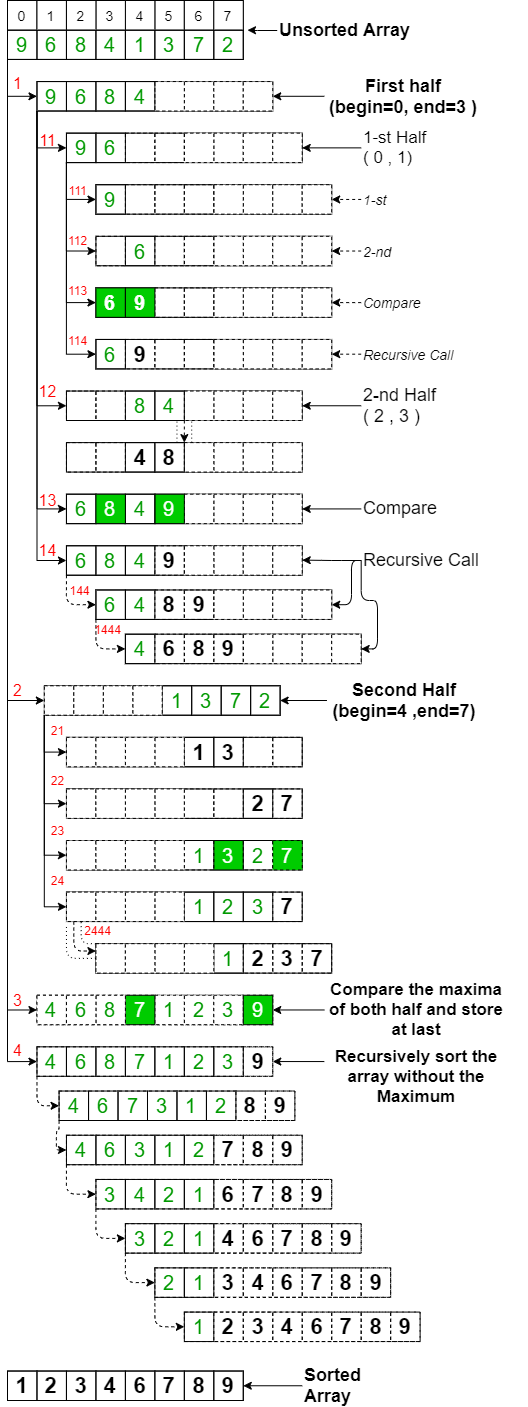
Clasificación lenta
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <iostream>
using namespace std;
// Function to swap two elements
void swap(int* xp, int* yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
// Function to sort the array using
// the Slow sort
void slow_sort(int A[], int i, int j)
{
// Recursion break condition
if (i >= j)
return;
// Store the middle value
int m = (i + j) / 2;
// Recursively call with the
// left half
slow_sort(A, i, m);
// Recursively call with the
// right half
slow_sort(A, m + 1, j);
// Swap if the first element is
// lower than second
if (A[j] < A[m]) {
swap(&A[j], &A[m]);
}
// Recursively call with the
// array excluding the maximum
// element
slow_sort(A, i, j - 1);
}
// Function to print the array
void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
// Driver Code
int main()
{
// Given Input
int arr[] = { 6, 8, 9, 4, 12, 1 };
int n = sizeof(arr) / sizeof(arr[0]);
// Function Call
slow_sort(arr, 0, n - 1);
// Print the sorted array
printArray(arr, n);
return 0;
}
Java
// Java program for the above approach
class GFG{
// Function to sort the array using
// the Slow sort
static void slow_sort(int A[], int i, int j)
{
// Recursion break condition
if (i >= j)
return;
// Store the middle value
int m = (i + j) / 2;
// Recursively call with the
// left half
slow_sort(A, i, m);
// Recursively call with the
// right half
slow_sort(A, m + 1, j);
// Swap if the first element is
// lower than second
if (A[j] < A[m])
{
int temp = A[j];
A[j] = A[m];
A[m] = temp;
}
// Recursively call with the
// array excluding the maximum
// element
slow_sort(A, i, j - 1);
}
// Function to print the array
static void printArray(int arr[], int size)
{
int i;
for(i = 0; i < size; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver code
public static void main(String[] args)
{
int arr[] = { 6, 8, 9, 4, 12, 1 };
int n = arr.length;
// Function Call
slow_sort(arr, 0, n - 1);
// Print the sorted array
printArray(arr, n);
}
}
// This code is contributed by abhinavjain194
Python3
# Python3 program for the above approach # Function to sort the array using # the Slow sort def slow_sort(A, i, j): # Recursion break condition if (i >= j): return # Store the middle value m = (i + j) // 2 # Recursively call with the # left half slow_sort(A, i, m) # Recursively call with the # right half slow_sort(A, m + 1, j) # Swap if the first element is # lower than second if (A[j] < A[m]): temp = A[m] A[m] = A[j] A[j] = temp # Recursively call with the # array excluding the maximum # element slow_sort(A, i, j - 1) # Function to print the array def printArray(arr, size): for i in range(size): print(arr[i], end = " ") # Driver Code if __name__ == '__main__': arr = [ 6, 8, 9, 4, 12, 1 ] n = len(arr) # Function Call slow_sort(arr, 0, n - 1) # Print the sorted array printArray(arr, n) # This code is contributed by SoumikMondal
C#
// C# implementation of the approach
using System;
class GFG
{
// Function to sort the array using
// the Slow sort
static void slow_sort(int[] A, int i, int j)
{
// Recursion break condition
if (i >= j)
return;
// Store the middle value
int m = (i + j) / 2;
// Recursively call with the
// left half
slow_sort(A, i, m);
// Recursively call with the
// right half
slow_sort(A, m + 1, j);
// Swap if the first element is
// lower than second
if (A[j] < A[m])
{
int temp = A[j];
A[j] = A[m];
A[m] = temp;
}
// Recursively call with the
// array excluding the maximum
// element
slow_sort(A, i, j - 1);
}
// Function to print the array
static void printArray(int[] arr, int size)
{
int i;
for(i = 0; i < size; i++)
Console.Write(arr[i] + " ");
Console.WriteLine();
}
// Driver code
public static void Main()
{
int[] arr = { 6, 8, 9, 4, 12, 1 };
int n = arr.Length;
// Function Call
slow_sort(arr, 0, n - 1);
// Print the sorted array
printArray(arr, n);
}
}
// this code is contributed by sanjoy_62.
Javascript
<script>
// JavaScript program for the above approach
// Function to sort the array using
// the Slow sort
function slow_sort(A, i, j)
{
// Recursion break condition
if (i >= j)
return;
// Store the middle value
let m = parseInt((i + j) / 2, 10);
// Recursively call with the
// left half
slow_sort(A, i, m);
// Recursively call with the
// right half
slow_sort(A, m + 1, j);
// Swap if the first element is
// lower than second
if (A[j] < A[m])
{
let temp = A[j];
A[j] = A[m];
A[m] = temp;
}
// Recursively call with the
// array excluding the maximum
// element
slow_sort(A, i, j - 1);
}
// Function to print the array
function printArray(arr, size)
{
let i;
for(i = 0; i < size; i++)
document.write(arr[i] + " ");
document.write("</br>");
}
let arr = [ 6, 8, 9, 4, 12, 1 ];
let n = arr.length;
// Function Call
slow_sort(arr, 0, n - 1);
// Print the sorted array
printArray(arr, n);
</script>
Producción:
1 4 6 8 9 12
Complejidad de tiempo de mejor caso: ![]() , donde e > 0
, donde e > 0
Complejidad de tiempo de caso promedio: ![]()
Espacio auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por scorchingeagle y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA