Este es un documento de ubicación del modelo TCS para la preparación de aptitudes. Este documento de colocación cubrirá las preguntas de aptitud que se hacen en las campañas de reclutamiento de TCS y también sigue estrictamente el patrón de preguntas que se hacen en las entrevistas de TCS. Se recomienda resolver cada una de las siguientes preguntas para aumentar sus posibilidades de aprobar la entrevista de TCS.

- Un agente de un centro de llamadas tiene una lista de 305 números de teléfono de personas en orden alfabético de nombres, pero Anuj no tiene ninguno de los nombres. Necesita comunicarse rápidamente con Danish Mank para transmitirle un mensaje. Si cada llamada tarda 2 minutos en completarse y todas las llamadas son respondidas, ¿cuál es la cantidad mínima de tiempo durante la cual puede garantizar entregar el mensaje a Danish?
a) 206 minutos
b) 610 minutos
c) 18 minutos
d) 34 minutos
Answer: c) 18 minutes
Solución:
Necesitamos buscar un nombre en particular en una guía telefónica. Por lo tanto, debemos aplicar un método en el que podamos buscar fácilmente un número en un recuento mínimo. Entonces, dividimos la lista en dos mitades iguales, es decir, 305/2 = 152.5 o tomemos 152. Ahora podemos decidir si buscamos danés en la mitad superior o inferior de 152. Esto se decide por la letra inicial del nombre en una pagina Procediendo de manera similar obtenemos,
152/2 = 76
76/2 = 38
38/2 = 19
19/2 = 9
9/2 = 4
4/2 = 2
2/2 = 0
Entonces obtenemos 0 en el noveno tiempo, por lo tanto, este es el número mínimo de la cuenta para encontrar danés. Así que el tiempo total empleado = 9 * 2 = 18 minutos.
2. Hay una oficina que consta de 38 personas. A 10 de ellos les gusta jugar al golf, a 15 les gusta jugar al fútbol y 20 no juegan ni al golf ni al fútbol. ¿A cuántos les gusta tanto el golf como el fútbol?
a) 10
b) 7
c) 15
d) 18
Answer: b) 7
Solución:
Sea el número de personas a las que les gusta el golf = ‘A’
Sea el número de personas a las que les gusta el fútbol = ‘B’
Sea el número de personas a las que les gusta el golf o el fútbol = AUB = 38 – 20 = 18 A
las personas les gusta tanto el golf como el fútbol =
= A + B – AUB = 10 + 15 -18 = 7
3. Si se lanza un dado 2 veces, ¿cuál es la probabilidad de obtener un par de números cuya suma sea 3 o 4?
a) 6/36
b) 5/36
c) 1/9
d) 1/12
Answer: b) 5/36
Solución:
Probabilidad total = 36
Podemos obtener una suma de 3 o 4 de estas muchas maneras:
=> (2, 1), (1, 2), (1, 3), (3, 1), (2, 2) ) = 5
Entonces probabilidad = 5 / 36
4. Un comerciante cobra 12 rupias por un montón de pasteles. Anuj regateó con el tendero y obtuvo dos más, y eso hizo que costaran una rupia por docena menos que el primer precio solicitado. ¿Cuántos pasteles recibió Anuj en 12 rupias?
a) 10
b) 14
c) 18
d) 16
Answer: d) 16
Solución:
Sea el número de pasteles = ‘x’ o ‘x/12’ docenas
Entonces, x/12 le cuesta a Anuj 12 rupias, o 1 docena le cuesta = 144/x rupias
Ahora, recibe dos extra = 144/(x+ 2) en 1 rupia menos,
=> 144/x – 144/(x+2) = 1
=> Al poner 16 se cumple la ecuación, de ahí la respuesta.
5. Ram solo puede hacer 1/4 del trabajo en 2 días. Solo Shyam puede hacer 2/3 del trabajo en 4 días. Entonces, ¿qué parte del trabajo debe hacer Anil en 2 días para que completen el trabajo juntos en 3 días?
a) 1/8
b) 1/20
c) 1/16
d) 1/12
Respuesta: d) 1/12
Solución:
Solo Ram puede completar el trabajo en 2*4 = 8 días.
Solo Shyam puede completar el trabajo en 4*(3/2) = 6 días.
Tomando el mcm de 8, 6, 3 = 24
Capacidad de Ram = 24/8 = 3
Capacidad de Shyam = 24/6 = 4
Capacidad de Anil = 8 – (4+3) = 1
Ahora en 2 días Anil puede hacer 2 unidad de trabajo = 2/24 = 1/12 parte del trabajoO
Sea x el trabajo de un día de C.
Cuenta preguntar
1/8 + 1/6 + x = 1/3
X = 1/24
Por lo tanto C completará 1/12 del trabajo en 2 días.
6. El Sr. Mehta elige un número y sigue duplicando el número seguido de restarle uno. Si elige el 3 como número inicial y repite la operación 30 veces, ¿cuál es el resultado final?
a) (2^30) – 1
b) (2^30) – 2
c) (2^31) – 1
d) Ninguno de estos
Answer: d) None of these
Solución:
Según la pregunta,
3 * 2 – 1 = 5 =
5 * 2 – 1 = 9 =
9 * 2 – 1 = 17 =
Procediendo de manera similar, en 30 veces obtenemos
7. Solo Ram puede pintar una pared en 7 días y su amigo Roy solo pinta la misma pared en 9 días. ¿En cuántos días pueden pintar la pared trabajando juntos? (Redondee su respuesta)
a) 3
b) 5
c) 4
d) 7
Answer: c) 4
Solución:
Esto se puede resolver aplicando una fórmula simple = ab/(a+b)
o, (9*7)/(9+7)
o, 63/16 = 3.9375 = 4 (respuesta)
8. Dos paredes verticales de 6 metros y 11 metros de largo están separadas por una distancia de 12 metros. ¿Encuentra la distancia superior de ambas paredes?
a) 15 metros
b) 13 metros
c) 12 metros
d) 10 metros
Answer: b) 13 meters
Solución:
Consideremos esta figura,
Necesitamos encontrar la distancia de AB.
Sabemos que AC = 12 m y BC = 11-6 = 5 m
Entonces, aplicando el teorema de Pitágoras obtenemos,
AB =
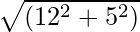
= 13 metros
9. Para f(m, n) =45*m + 36*n, donde m y n son números enteros (positivos o negativos). ¿Cuál es el valor positivo mínimo para f(m, n) para todos los valores de m, n (esto se puede lograr para varios valores de m y n)?
a) 18
b) 12
c) 9
d) 16
Answer: c) 9
Solución:
Para obtener el valor mínimo de f(m, n), ponemos m = 1 y n = -1, obtenemos
f(, n) = 9
10. Un cubo blanco (con seis caras) debe pintarse de azul en dos caras diferentes. ¿De cuántas maneras diferentes se puede lograr esto (dos cuadros se consideran iguales si en una rotación adecuada del cubo se puede llevar un cuadro al otro)?
a) 30 vías
b) 18 vías
c) 4 vías
d) 2 vías
Answer: d) 2
Solución:
Esto se puede lograr de las siguientes maneras diferentes:
Primero, pintar en caras opuestas se puede lograr de una manera.
En segundo lugar, la pintura en caras adyacentes se puede lograr de 1 manera.
Por lo tanto de 2 maneras.
Publicación traducida automáticamente
Artículo escrito por Chinmoy Lenka y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
