Papel de colocación TCS | MCQ 6

Este es un documento de ubicación del modelo TCS para la preparación de aptitudes. Este documento de colocación cubrirá las preguntas de aptitud que se hacen en las campañas de reclutamiento de TCS y también sigue estrictamente el patrón de preguntas que se hacen en las entrevistas de TCS. Se recomienda resolver cada una de las siguientes preguntas para aumentar sus posibilidades de aprobar la entrevista de TCS.

Crusoe salió del cascarón de un misterioso huevo descubierto por Angus que estaba creciendo a un ritmo tan rápido que Angus tuvo que trasladarlo desde su casa hasta el lago. Dados los pesos de Crusoe en sus primeras semanas de nacimiento como 5, 15, 30, 135, 405, 1215, 3645. Encuentra el peso impar.
a) 3645
b) 135
c) 15
d) 30
```
Answer: d) 30
```
Solución:
Al observar la serie de cerca, encontramos que el tercer número está colocado de manera extraña.
La serie tiene la forma:
5 * 3 = 15
15 * 3 = 45
45 * 3 = 135
135 * 3 = 405 y así sucesivamente
Suponga que f(1)=0 y f(m+n)=f(m)+f(n)+4(9mn-1). Para todos los números naturales (Enteros>0)m y n. ¿Cuál es el valor de f(17)?
a) 5436
b) 4831
c) 5508
d) 4832
```
Answer: d) 4832
```
Solución:
Necesitamos usar f(1) para calcular el valor de f(17)
f(17) se puede escribir como f(1+16)
f(16) se puede escribir como f(8+8)
f(8 ) se puede escribir como f(4+4)
f(4) se puede escribir como f(2+2)
f(2) se puede escribir como f(1+1)
f(1) = 0, entonces f(2 ) = f(1+1) = f(1)+f(1)+4(9*1*1-1) = 32.
o f(4) = f(2+2) = f(2) +f(2)+4(9×2×2 – 1) = 32+32+4×35 = 204.
o f(8) = f(4+4) = f(4)+f(4) +4(9×4×4 – 1) = 204+204+4×143 = 980
o f(16) = f(8+8) = f(8)+f(8)+4(9×8 ×8 – 1) = 980+980+4×575 = 4260
o f(17) = f(1+16) = f(16)+f(1)+4(9×16×1 –1) = 4260+0+ 4×143 = 4832
Una suma de Rs.3000 se distribuye entre P, Q y R. P obtiene 2/3 de lo que juntaron Q y R y R recibe 1/3 de lo que juntaron P y Q, ¿la parte de R es?
a) 750
b) 850
c) 800
d) 700
```
Answer: a) 750
```
Solución:
De acuerdo a la pregunta,
caso 1: P = 2(Q + R)/3
o, (Q+R)/P = 3/2
caso 2: También, R = (P+Q)/3
o, ( P+Q)/R = 3/1
Simplemente usando componente-dividendo, obtenemos,
para el caso 1, (P+Q+R)/P = 3+2/2 = 5/2 = 20/8
para el caso 2, (P+Q+R)/R = 3+1/1 = 4/1 = 20/5
Al resolver obtenemos, P = 8, Q = 7, R = 5
o la parte de R = 5/(8+7+ 5) * 3000 = 750
En la serie dada 11, 23, 47, 83, 131, … ¿Cuál es el siguiente número?
a) 145
b) 178
c) 191
d) 176
```
Answer: c) 191
```
Solución:

La serie dada sigue el orden de múltiplo de 12
23 – 11 = 12
47 – 23 = 24
83 – 47 = 36
131 – 83 = 48
x – 131 = 60
o x = 191
si un numero se divide por 357 el resto es 5 cual sera el resto si el numero se divide por 17
a) 9
b) 3
c) 7
d) 5
```
Answer: d) 5 
```
Solución:
Sea el número N cuando dividido por 357 deja resto 5 y cociente q.
Entonces, N = 357k + 5 = 17 * 21 * k + 5
Entonces, 357 es exactamente divisible por 17, por lo que el resto es 5
Un poste de 36 m de altura está en un borde de un camino roto a cierta altura. Cayó de tal manera que la parte superior del poste toca el otro borde del camino. Si el ancho del camino es de 12 m, ¿cuál es la altura a la que se rompió el poste?
a) 12
b) 16
c) 24
d) 18
```
Answer: b) 16
```
Solución:
Sea el punto en el que se rompió el poste a ‘x’ del suelo, de modo que la longitud de la pieza rota sea (36-x).
Entonces aplicando el teorema de Pitágoras obtenemos,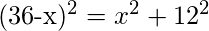 $(36-x)^2 = x^2 + 12^2$
=> $1296 + x^2 - 72x = x^2 + 144$
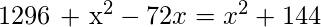
=> 72x = 1296 – 144
=> x = 16
Hay un salón que consta de 23 personas. Se dan la mano juntos. Entonces, ¿cuántos apretones de manos son posibles si están en un par de secuencia cíclica?
a) 23
b) 22
c) 253
d) 250
```
Answer: c) 253
```
Solución:
Como hay 23 personas, número de apretones de manos posibles = 23C2 = 253 apretones de manos.
En un sótano hay algunas bicicletas y coches. El martes hay 182 ruedas en el sótano. ¿Cuantas bicicletas hay?
a) 20
b) 19
c) 18
d) 16
```
Answer: b) 19
```
Solución:
Esta es una pregunta muy ambigua y debe calcularse usando las opciones.
Si hay 20 bicicletas, debe haber 20*2 = 40 ruedas Ruedas
restantes = 182-40 = 142 ruedas = 142/4 no es un número entero por lo que no puede haber 20 bicicletas.
De manera similar, verificando 19 bicicletas = 19 * 2 = 38 ruedas Ruedas
restantes = 182 – 38 = 144 = 144/4 = 36 autos, por lo tanto, esta es la respuesta.
Hay un terreno rectangular de 17 × 8 m rodeado por un camino de 1,5 m de ancho. La profundidad del camino es de 12 cm. Se llena de arena y encuentre la cantidad de arena requerida.
a) 5,5
b) 10,08
c) 6,05
d) 7,05
```
Answer: b) 10.08
```
Solución:
Área del rectángulo interior = 17 * 8 = 136 metros cuadrados
Área del rectángulo exterior = (17 + 2*1,5) * (8 * 2*1,5) = 220 metros cuadrados
Así que el área del camino restante = 220 – 136 = 84 metros cuadrados
Entonces se requiere arena para llenar el camino = 84 * (12/100) = 10.08 metros cuadrados
Los números 272738 y 232342, cuando se dividen por n, un número de dos dígitos, dejan un resto de 13 y 17 respectivamente. Encuentra la suma de los dígitos de n?
a) 5
b) 4
c) 7
d) 8
```
Answer: c) 7
```
Solución:
De acuerdo con la pregunta, (272738 – 13) y (232342 – 17) son exactamente divisibles por n.
Entonces, si encontramos el HCF de estos dos números, obtenemos n,
El HCF de 272725 y 232325 es 25
Entonces la suma de los dígitos = 7.

Publicación traducida automáticamente

Artículo escrito por Chinmoy Lenka y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta