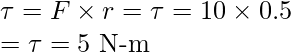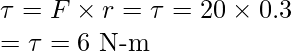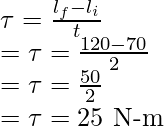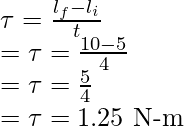Para un cuerpo rígido, el movimiento es generalmente tanto de rotación como de traslación. Si el cuerpo está fijo en un punto, el movimiento suele ser de rotación. Se sabe que se necesita fuerza para cambiar el estado de traslación del cuerpo y proporcionarle una aceleración lineal. El par y el momento angular son equivalentes rotacionales de la fuerza y el momento. Estas entidades nos ayudan a cambiar el estado de rotación del cuerpo. Los pares y el momento angular son muy útiles y se encuentran en casi todas partes en la vida diaria. La potencia del motor y los motores se mide por el par. Entonces, al estudiar cualquier cuerpo rígido, es esencial comprender los conceptos de par y momento angular. Veamos estos conceptos en detalle.
Esfuerzo de torsión
El par es análogo a la fuerza en el caso del movimiento de rotación. Considere un ejemplo de una puerta. La posición de la puerta es fija, solo puede girar alrededor de su eje. Entonces, ¿qué hace que la puerta gire? Se requiere fuerza, pero la fuerza aplicada a la bisagra de la puerta no funciona. Entonces, no es solo la fuerza, la posición a la que se aplica también importa.
En el movimiento de rotación, la fuerza análoga es el par. Esto también se llama el momento de la fuerza. Esto provoca una aceleración angular en el cuerpo, lo que significa obligar a cambiar el estado de rotación del cuerpo. Sea una partícula P situada lejos del origen en un punto cuyo vector de posición viene dado por ![]() . Si la fuerza F actúa sobre la partícula, el momento de fuerza está dado por,
. Si la fuerza F actúa sobre la partícula, el momento de fuerza está dado por,
![]()
Dado que el producto cruzado está involucrado, es una cantidad vectorial. La magnitud del torque está dada por,
![]()
Aquí, “r” es la magnitud del vector de posición y es el ángulo entre el vector de posición y la fuerza. En la fórmula, la parte «rsin» es la distancia perpendicular de la fuerza desde el eje del cuerpo rígido.
Las dimensiones del par están dadas por ML 2 T -2 . Estas también son dimensiones de energía, pero estas cantidades no deben confundirse como similares. Son magnitudes muy diferentes. La unidad de par es Nm.
Momento angular de partícula
Se ha mencionado que el momento de torsión es análogo a la fuerza. De la misma manera, el momento angular es análogo al momento lineal. Este también es un producto vectorial similar a su par homólogo. Considere una partícula P con el momento lineal «p» y un vector de posición con respecto al origen O. El momento angular de la partícula se denota por «L»,
L = r × p
La magnitud del momento angular estará dada por,
L = rpsin
Donde r y p son las magnitudes del vector de posición y el momento lineal respectivamente. El ángulo es el ángulo entre el vector de posición y el momento lineal. Aquí también “rsin()” es el ángulo perpendicular entre el momento y el vector de posición.
Relación entre el momento angular y el par
La relación entre el momento angular y el momento de torsión es similar a la relación entre la fuerza y el momento. La fuerza es el cambio en el momento de la partícula. De manera similar, el torque es el cambio en el momento angular de la partícula. Derivando la fórmula para el momento angular,
![]()
Aplicando la regla del producto para la diferenciación,
![]()
Ahora, ![]() es la velocidad de la partícula, pero como está en la misma dirección que el impulso,
es la velocidad de la partícula, pero como está en la misma dirección que el impulso,
rx ![]() = 0
= 0
Entonces, ahora la ecuación se convierte en,
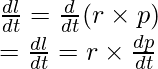
![]() represents the force F,
represents the force F,
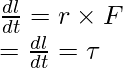
Por lo tanto, esto prueba que la tasa de cambio del momento angular está dada por el par.
Problemas de muestra
Pregunta 1: Averigüe el par de torsión en la puerta si se aplica una fuerza de 10 N en la puerta a 0,5 m de la bisagra.
Responder:
El par está dado por,
Donde r es la distancia perpendicular de la fuerza desde el eje de rotación.
Dado: r = 0.5m y F = 10N.
Reemplazando los valores en la ecuación,
Pregunta 2: Averigüe el par de torsión en la puerta si se aplica una fuerza de 20 N en la puerta a 0,3 m de la bisagra.
Responder:
El par está dado por,
Donde r es la distancia perpendicular de la fuerza desde el eje de rotación.
Dado: r = 0.3m y F = 20N.
Reemplazando los valores en la ecuación,
Pregunta 3: Un cuerpo gira alrededor de un eje en un movimiento circular con un radio de 0,1 m, el momento del cuerpo está dado por 50 Kgm/s. Encuentre el momento angular del cuerpo.
Responder:
El momento angular de un cuerpo está dado por,
l = r × pag
Donde r es la distancia perpendicular de la fuerza desde el eje de rotación y p es el momento lineal.
Dado: r = 0.3m yp = 50Kgm/s.
Reemplazando los valores en la ecuación,
l = r xp
⇒l =0.3 × 50
⇒l = 15
Pregunta 4: Un cuerpo gira alrededor de un eje en un movimiento circular con un radio de 0,2 m, el momento del cuerpo está dado por 70 Kg/s. Encuentre el momento angular del cuerpo.
Responder:
El momento angular de un cuerpo está dado por,
l = r × pag
Donde r es la distancia perpendicular de la fuerza desde el eje de rotación y p es el momento lineal.
Dado: r = 0.2m yp =70 Kg/s.
Reemplazando los valores en la ecuación,
l = r × pag
⇒l =0.2 × 70
⇒l = 14
Pregunta 5: Un cuerpo gira alrededor de un eje en un movimiento circular con un radio de 0,2 m, el momento del cuerpo está dado por 70 Kg/s. Se aplica un par de torsión sobre el cuerpo durante 2 segundos y la cantidad de movimiento se convierte en 120 kgm/s. Encuentre el torque aplicado al cuerpo.
Responder:
El momento angular de un cuerpo está dado por,
l = r × pag
Donde r es la distancia perpendicular de la fuerza desde el eje de rotación y p es el momento lineal.
La tasa de cambio en el momento angular nos da el par.
Momento angular inicial
l yo = 0. 2 × 70
yo = 14
Momento angular final
l yo = 0. 2 × 120
yo = 24
Tasa de cambio del momento angular =
Pregunta 6: Un cuerpo gira alrededor de un eje en un movimiento circular con un radio de 0,1 m, el momento del cuerpo está dado por 50 Kgm/s. Se aplica un par de torsión sobre el cuerpo durante 4 segundos y la cantidad de movimiento se convierte en 100 kgm/s. Encuentre el torque aplicado al cuerpo.
Responder:
El momento angular de un cuerpo está dado por,
l = r × pag
Donde r es la distancia perpendicular de la fuerza desde el eje de rotación y p es el momento lineal.
La tasa de cambio en el momento angular nos da el par.
Momento angular inicial
l yo = 0. 1 × 50
yo = 5
Momento angular final
l yo = 0. 1 × 100
yo = 10
Tasa de cambio del momento angular =
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA