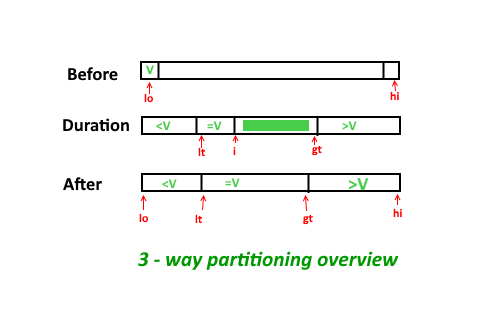
Dada una array y un rango [ lowVal , highVal ], divida la array alrededor del rango de modo que la array se divida en tres partes.
- Todos los elementos más pequeños que lowVal vienen primero.
- Todos los elementos en el rango lowVal a highVal vienen a continuación.
- Todos los elementos mayores que highVVal aparecen al final.
- El orden relativo de los números no debe cambiarse.
Ejemplos:
Entrada: arr[] = {1, 14, 5, 20, 4, 2, 54, 20, 87, 98, 3, 1, 32}, lowVal = 14, highVal = 20
Salida: arr[] = { 1 5 4 2 3 1 14 20 20 54 87 98 32 }Entrada: arr[] = {1, 14, 5, 20, 4, 2, 54, 20, 87, 98, 3, 1, 32}, lowVal = 20, highVal = 20
Salida: arr[] = { 1 14 5 4 2 3 1 20 20 54 87 98 32 }
Enfoque: este enfoque se basa en el uso de estructuras de datos adicionales para almacenar los elementos menores que lowVal, entre lowVal y highVal, y elementos mayores que highVal. Usaremos 3 colas para mantener el orden original de los elementos.
- Atraviesa la array uno por uno
- Inserte los elementos de la array en la cola respectiva uno por uno
- Al final,
- Saque todos los elementos en la cola 1 con elementos menores que lowVal
- Luego saca todos los elementos en la cola 2 con elementos entre lowVal y highVal
- Luego saque todos los elementos en la cola 3 con elementos mayores que highVal.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ code to implement three way
// partitioning of an array without
// changing the relative ordering
#include <bits/stdc++.h>
using namespace std;
// Function to do three way partitioning
vector<int> pivotArray(vector<int>& nums, int lowVal,
int highVal)
{
// Declaring 3 queues
queue<int> before, same, after;
// Traverse the array elements one by one
for (int i = 0; i < nums.size(); i++) {
// If the element is
// less than pivot range
// insert it into queue before
if (nums[i] < lowVal)
before.push(nums[i]);
// Else If the element is
// in between pivot range
// insert it into queue same
else if (nums[i] > highVal)
after.push(nums[i]);
// Else If the element is
// less than pivot range
// insert it into queue after
else
same.push(nums[i]);
}
int k = 0;
// Now insert all elements
// in queue before and
// insert into final vector
while (before.size() > 0) {
nums[k++] = before.front();
before.pop();
}
// Now insert all elements
// in queue same and
// insert into final vector
while (same.size() > 0) {
nums[k++] = same.front();
same.pop();
}
// Now insert all elements
// in queue after and
// insert into final vector
while (after.size() > 0) {
nums[k++] = after.front();
after.pop();
}
// Return the final vector
return nums;
}
// Driver code
int main()
{
vector<int> arr
= { 1, 14, 5, 20, 4, 2, 54,
20, 87, 98, 3, 1, 32 };
int lowVal = 20, highVal = 20;
pivotArray(arr, lowVal, highVal);
for (int i = 0; i < arr.size(); i++) {
cout << arr[i] << " ";
}
return 0;
}
Java
// JAVA code to implement three way
// partitioning of an array without
// changing the relative ordering
import java.util.*;
class GFG {
// Function to do three way partitioning
public static int[] pivotArray(int[] nums, int lowVal,
int highVal)
{
// Declaring 3 queues
Queue<Integer> before = new LinkedList<>();
Queue<Integer> same = new LinkedList<>();
Queue<Integer> after = new LinkedList<>();
// Traverse the array elements one by one
for (int i = 0; i < nums.length; i++) {
// If the element is
// less than pivot range
// insert it into queue before
if (nums[i] < lowVal)
before.add(nums[i]);
// Else If the element is
// in between pivot range
// insert it into queue same
else if (nums[i] > highVal)
after.add(nums[i]);
// Else If the element is
// less than pivot range
// insert it into queue after
else
same.add(nums[i]);
}
int k = 0;
// Now insert all elements
// in queue before and
// insert into final vector
while (before.size() > 0) {
nums[k++] = before.poll();
}
// Now insert all elements
// in queue same and
// insert into final vector
while (same.size() > 0) {
nums[k++] = same.poll();
}
// Now insert all elements
// in queue after and
// insert into final vector
while (after.size() > 0) {
nums[k++] = after.poll();
}
// Return the final vector
return nums;
}
// Driver code
public static void main(String[] args)
{
int arr[] = new int[] { 1, 14, 5, 20, 4, 2, 54,
20, 87, 98, 3, 1, 32 };
int lowVal = 20, highVal = 20;
pivotArray(arr, lowVal, highVal);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
// This code is contributed by Taranpreet
Python3
# Python 3 code to implement three way # partitioning of an array without # changing the relative ordering # Function to do three way partitioning def pivotArray(nums, lowVal, highVal): # Declaring 3 queues before = [] same = [] after = [] # Traverse the array elements one by one for i in range(len(nums)): # If the element is # less than pivot range # insert it into queue before if (nums[i] < lowVal): before.append(nums[i]) # Else If the element is # in between pivot range # insert it into queue same elif (nums[i] > highVal): after.append(nums[i]) # Else If the element is # less than pivot range # insert it into queue after else: same.append(nums[i]) k = 0 # Now insert all elements # in queue before and # insert into final vector while (len(before) > 0): nums[k] = before[0] k += 1 before.pop(0) # Now insert all elements # in queue same and # insert into final vector while (len(same) > 0): nums[k] = same[0] same.pop(0) k += 1 # Now insert all elements # in queue after and # insert into final vector while (len(after) > 0): nums[k] = after[0] k += 1 after.pop(0) # Return the final vector return nums # Driver code if __name__ == "__main__": arr = [1, 14, 5, 20, 4, 2, 54, 20, 87, 98, 3, 1, 32] lowVal = 20 highVal = 20 pivotArray(arr, lowVal, highVal) for i in range(len(arr)): print(arr[i], end=" ") # This code is contributed by ukasp.
C#
// C# code to implement three way
using System;
using System.Collections;
public class GFG{
// partitioning of an array without
// changing the relative ordering
// Function to do three way partitioning
static int[] pivotArray(int[] nums, int lowVal,
int highVal)
{
// Declaring 3 queues
Queue before = new Queue();
Queue same = new Queue();
Queue after = new Queue();
// Traverse the array elements one by one
for (int i = 0; i < nums.Length; i++) {
// If the element is
// less than pivot range
// insert it into queue before
if (nums[i] < lowVal)
before.Enqueue(nums[i]);
// Else If the element is
// in between pivot range
// insert it into queue same
else if (nums[i] > highVal)
after.Enqueue(nums[i]);
// Else If the element is
// less than pivot range
// insert it into queue after
else
same.Enqueue(nums[i]);
}
int k = 0;
// Now insert all elements
// in queue before and
// insert into final vector
while (before.Count > 0) {
nums[k++] = (int)before.Peek();
before.Dequeue();
}
// Now insert all elements
// in queue same and
// insert into final vector
while (same.Count > 0) {
nums[k++] = (int)same.Peek();
same.Dequeue();
}
// Now insert all elements
// in queue after and
// insert into final vector
while (after.Count > 0) {
nums[k++] = (int)after.Peek();
after.Dequeue();
}
// Return the final vector
return nums;
}
// Driver code
static public void Main (){
int [ ] arr
= { 1, 14, 5, 20, 4, 2, 54,
20, 87, 98, 3, 1, 32 };
int lowVal = 20, highVal = 20;
pivotArray(arr, lowVal, highVal);
for (int i = 0; i < arr.Length; i++) {
Console.Write(arr[i] + " ");
}
}
}
// This code is contributed by hrithikgarg03188.
Javascript
<script>
// JavaScript code to implement three way
// partitioning of an array without
// changing the relative ordering
// Function to do three way partitioning
const pivotArray = (nums, lowVal, highVal) => {
// Declaring 3 queues
let before = [], same = [], after = [];
// Traverse the array elements one by one
for (let i = 0; i < nums.length; i++) {
// If the element is
// less than pivot range
// insert it into queue before
if (nums[i] < lowVal)
before.push(nums[i]);
// Else If the element is
// in between pivot range
// insert it into queue same
else if (nums[i] > highVal)
after.push(nums[i]);
// Else If the element is
// less than pivot range
// insert it into queue after
else
same.push(nums[i]);
}
let k = 0;
// Now insert all elements
// in queue before and
// insert into final vector
while (before.length > 0) {
nums[k++] = before[0];
before.shift();
}
// Now insert all elements
// in queue same and
// insert into final vector
while (same.length > 0) {
nums[k++] = same[0];
same.shift();
}
// Now insert all elements
// in queue after and
// insert into final vector
while (after.length > 0) {
nums[k++] = after[0];
after.shift();
}
// Return the final vector
return nums;
}
// Driver code
let arr = [1, 14, 5, 20, 4, 2, 54,
20, 87, 98, 3, 1, 32];
let lowVal = 20, highVal = 20;
pivotArray(arr, lowVal, highVal);
for (let i = 0; i < arr.length; i++) {
document.write(`${arr[i]} `);
}
// This code is contributed by rakeshsahni
</script>
1 14 5 4 2 3 1 20 20 54 87 98 32
Complejidad de tiempo: O(N), donde N es el tamaño de la array.
Espacio Auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por krishmurarka y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA