Dado un número n de archivos ordenados, la tarea es encontrar los cálculos mínimos realizados para alcanzar el patrón de combinación óptimo.
Cuando se van a fusionar dos o más archivos ordenados para formar un solo archivo, los cálculos mínimos que se realizan para llegar a este archivo se conocen como patrón de fusión óptimo .
Si es necesario fusionar más de 2 archivos, se puede hacer en pares. Por ejemplo, si necesita fusionar 4 archivos A, B, C, D. Primero fusione A con B para obtener X1, fusione X1 con C para obtener X2, fusione X2 con D para obtener X3 como archivo de salida.
Si tenemos dos archivos de tamaño m y n, el tiempo total de cálculo será m+n. Aquí, usamos la estrategia codiciosa al fusionar los dos archivos de menor tamaño entre todos los archivos presentes.
Ejemplos:
dados 3 archivos con tamaños de 2, 3, 4 unidades. Encuentre una forma óptima de combinar estos archivos
Entrada: n = 3, tamaño = {2, 3, 4}
Salida: 14
Explicación: Hay diferentes formas de combinar estos archivos:
Método 1: Método óptimo
Método 2:
Método 3:
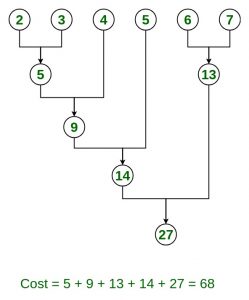
Entrada: n = 6, tamaño = {2, 3, 4, 5, 6, 7}
Salida: 68
Explicación: forma óptima de combinar estos archivos
Entrada: n = 5, tamaño = {5,10,20,30,30}
Salida: 205Entrada: n = 5, tamaño = {8,8,8,8,8}
Salida: 96
Observaciones:
De los resultados anteriores, podemos concluir que para encontrar el costo mínimo de cómputo necesitamos tener nuestra array siempre ordenada, es decir, agregar el costo de cómputo mínimo posible y eliminar los archivos de la array. Podemos lograr esto de manera óptima utilizando una estructura de datos min-heap (priority-queue).
Acercarse:
El Node representa un archivo con un tamaño dado y los Nodes dados son mayores que 2
- Agregue todos los Nodes en una cola de prioridad (Min Heap).{pq.poll = tamaño de archivo}
- Inicializar recuento = 0 // variable para almacenar cálculos de archivos.
- Repetir mientras (el tamaño de la cola de prioridad es mayor que 1)
- peso int = pq.poll(); pq.pop;//pq denota cola de prioridad, elimina el primero más pequeño y saca (elimina)
- peso+=pq.encuesta() && pq.pop(); // agregue el segundo elemento y luego sáquelo (elimínelo)
- cuenta += peso;
- pq.add(weight) // agrega este costo combinado a la cola de prioridad;
- contar es la respuesta final
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to implement
// Optimal File Merge Pattern
#include <bits/stdc++.h>
using namespace std;
// Function to find minimum computation
int minComputation(int size, int files[])
{
// Create a min heap
priority_queue<int, vector<int>, greater<int> > pq;
for (int i = 0; i < size; i++) {
// Add sizes to priorityQueue
pq.push(files[i]);
}
// Variable to count total Computation
int count = 0;
while (pq.size() > 1) {
// pop two smallest size element
// from the min heap
int first_smallest = pq.top();
pq.pop();
int second_smallest = pq.top();
pq.pop();
int temp = first_smallest + second_smallest;
// Add the current computations
// with the previous one's
count += temp;
// Add new combined file size
// to priority queue or min heap
pq.push(temp);
}
return count;
}
// Driver code
int main()
{
// No of files
int n = 6;
// 6 files with their sizes
int files[] = { 2, 3, 4, 5, 6, 7 };
// Total no of computations
// do be done final answer
cout << "Minimum Computations = "
<< minComputation(n, files);
return 0;
}
// This code is contributed by jaigoyal1328
Java
// Java program to implement
// Optimal File Merge Pattern
import java.util.PriorityQueue;
import java.util.Scanner;
public class OptimalMergePatterns {
// Function to find minimum computation
static int minComputation(int size, int files[])
{
// create a min heap
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int i = 0; i < size; i++) {
// add sizes to priorityQueue
pq.add(files[i]);
}
// variable to count total computations
int count = 0;
while (pq.size() > 1) {
// pop two smallest size element
// from the min heap
int temp = pq.poll() + pq.poll();
// add the current computations
// with the previous one's
count += temp;
// add new combined file size
// to priority queue or min heap
pq.add(temp);
}
return count;
}
public static void main(String[] args)
{
// no of files
int size = 6;
// 6 files with their sizes
int files[] = new int[] { 2, 3, 4, 5, 6, 7 };
// total no of computations
// do be done final answer
System.out.println("Minimum Computations = "
+ minComputation(size, files));
}
}
Python3
# Python Program to implement # Optimal File Merge Pattern class Heap(): # Building own implementation of Min Heap def __init__(self): self.h = [] def parent(self, index): # Returns parent index for given index if index > 0: return (index - 1) // 2 def lchild(self, index): # Returns left child index for given index return (2 * index) + 1 def rchild(self, index): # Returns right child index for given index return (2 * index) + 2 def addItem(self, item): # Function to add an item to heap self.h.append(item) if len(self.h) == 1: # If heap has only one item no need to heapify return index = len(self.h) - 1 parent = self.parent(index) # Moves the item up if it is smaller than the parent while index > 0 and item < self.h[parent]: self.h[index], self.h[parent] = self.h[parent], self.h[parent] index = parent parent = self.parent(index) def deleteItem(self): # Function to add an item to heap length = len(self.h) self.h[0], self.h[length-1] = self.h[length-1], self.h[0] deleted = self.h.pop() # Since root will be violating heap property # Call moveDownHeapify() to restore heap property self.moveDownHeapify(0) return deleted def moveDownHeapify(self, index): # Function to make the items follow Heap property # Compares the value with the children and moves item down lc, rc = self.lchild(index), self.rchild(index) length, smallest = len(self.h), index if lc < length and self.h[lc] <= self.h[smallest]: smallest = lc if rc < length and self.h[rc] <= self.h[smallest]: smallest = rc if smallest != index: # Swaps the parent node with the smaller child self.h[smallest], self.h[index] = self.h[index], self.h[smallest] # Recursive call to compare next subtree self.moveDownHeapify(smallest) def increaseItem(self, index, value): # Increase the value of 'index' to 'value' if value <= self.h[index]: return self.h[index] = value self.moveDownHeapify(index) class OptimalMergePattern(): def __init__(self, n, items): self.n = n self.items = items self.heap = Heap() def optimalMerge(self): # Corner cases if list has no more than 1 item if self.n <= 0: return 0 if self.n == 1: return self.items[0] # Insert items into min heap for _ in self.items: self.heap.addItem(_) count = 0 while len(self.heap.h) != 1: tmp = self.heap.deleteItem() count += (tmp + self.heap.h[0]) self.heap.increaseItem(0, tmp + self.heap.h[0]) return count # Driver Code if __name__ == '__main__': OMP = OptimalMergePattern(6, [2, 3, 4, 5, 6, 7]) ans = OMP.optimalMerge() print(ans) # This code is contributed by Rajat Gupta
Minimum Computations = 68
Complejidad temporal: O(nlogn)
Espacio auxiliar: O(n)
Publicación traducida automáticamente
Artículo escrito por sparsh singhal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA