Peligros estáticos en lógica digital

Un peligro , si existe, en un circuito digital provoca una fluctuación temporal en la salida del circuito. En otras palabras, un peligro en un circuito digital es una perturbación temporal en el funcionamiento ideal del circuito que, si se le da algún tiempo, se resuelve por sí mismo. Estas perturbaciones o fluctuaciones ocurren cuando diferentes caminos desde la entrada hasta la salida tienen diferentes retrasos y debido a este hecho, los cambios en las variables de entrada no cambian la salida instantáneamente pero aparecen en la salida después de un pequeño retraso causado por los elementos de construcción del circuito, es decir, puertas lógicas.

Hay tres tipos diferentes de peligros que se encuentran en los circuitos digitales.

1. Peligro estático
2. Peligro dinámico
3. peligro funcional

Discutiremos solo los peligros estáticos aquí para comprenderlo completamente.

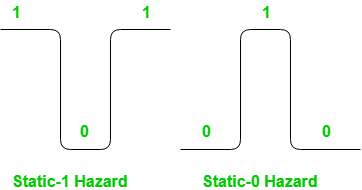
Formalmente, un peligro estático ocurre cuando el cambio en una entrada hace que la salida cambie momentáneamente antes de estabilizarse en su valor correcto. Según cuál sea el valor correcto, existen dos tipos de peligros estáticos, como se muestra a continuación en la imagen:

1. Peligro de estática 1: si la salida se encuentra actualmente en el estado lógico 1 y después de que la entrada cambia su estado, la salida cambia momentáneamente a 0 antes de establecerse en 1, entonces es un peligro de estática 1.
2. Riesgo de 0 estático: si la salida se encuentra actualmente en el estado lógico 0 y después de que la entrada cambia su estado, la salida cambia momentáneamente a 1 antes de establecerse en 0, entonces es un riesgo de 0 estático.

Detección de peligros estáticos usando K-map:
Consideremos primero el peligro estático-1. Para detectar un peligro de estática-1 para un circuito digital, se utilizan los siguientes pasos:

• Paso 1: escriba la salida del circuito digital, digamos Y.
• Paso 2: Dibuje el mapa K para esta función Y y observe todos los 1 adyacentes.
• Paso 3: si existe un par de celdas con 1 que no se encuentran en el mismo grupo (es decir, implicante principal), indica la presencia de un riesgo estático-1. Cada uno de estos pares es un peligro estático-1.

Tengamos un ejemplo:

Ejemplo: considere el circuito que se muestra a continuación.

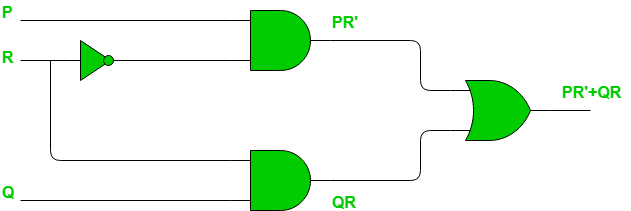
Tenemos salida, digamos F, como:
Dibujemos el mapa K para esta función booleana de la siguiente manera:

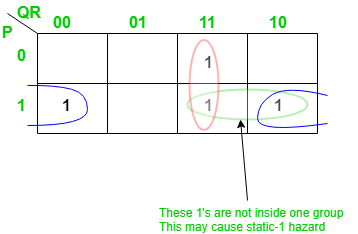
El par de 1 encerrado en verde no forma parte del agrupamiento/emparejamiento proporcionado por la salida de esta función booleana. Esto causará un peligro de estática-1 en este circuito.

Eliminación del peligro de estática-1:
una vez detectado, un peligro de estática-1 se puede eliminar fácilmente introduciendo algunos términos más (compuertas lógicas) a la función (circuito). La idea más común es agregar el grupo que falta en la función booleana existente, ya que agregar este término no afectaría la función de ninguna manera, pero eliminaría el peligro. Dado que en el ejemplo anterior, el par de 1 rodeado de color azul causa el riesgo de estática-1, simplemente agregamos esto como un implicante principal a la función existente de la siguiente manera:

Tenga en cuenta que no hay diferencia en el número de minitérminos de esta función. La razón es que los riesgos de 1 estático se basan en cómo agrupamos los 1 (o los 0 para el riesgo de 0 estático) para un conjunto dado de 1 en K-map. Por lo tanto, no hace ninguna diferencia en el número de 1 en K-map. El circuito se vería como se muestra a continuación con el cambio realizado para eliminar el riesgo de estática-1.

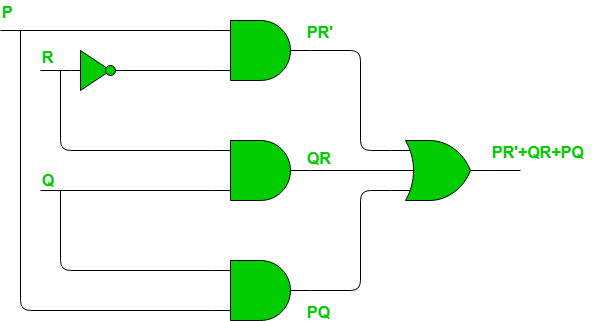
De manera similar, para los peligros de 0 estáticos, debemos considerar los 0 en lugar de los 1 y si algún 0 adyacente en K-map no está agrupado en el mismo grupo, puede causar un peligro de 0 estático. El método para detectar y resolver el peligro de estática-0 es completamente igual al que seguimos para el peligro de estática-1 excepto que en lugar de SOP, se usará POS ya que estamos tratando con 0 en este caso.