Requisito previo: ciclo hamiltoniano Dado un número entero n(>=2), encuentre una permutación de números del 1 al n tal que la suma de dos números consecutivos de esa permutación sea un cuadrado perfecto. Si ese tipo de permutación no es posible, imprima «Sin solución». Ejemplos:
Input : 17
Output : [16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17]
Explanation : 16+9 = 25 = 5*5, 9+7 = 16 = 4*4, 7+2 = 9 = 3*3 and so on.
Input: 20
Output: No Solution
Input : 25
Output : [2, 23, 13, 12, 24, 25, 11, 14, 22, 3, 1, 8,
17, 19, 6, 10, 15, 21, 4, 5, 20, 16, 9, 7, 18]
Método: Podemos representar un gráfico, donde los números del 1 al n son los Nodes del gráfico y hay una arista entre el i-ésimo y el j-ésimo Node si (i+j) es un cuadrado perfecto. Entonces podemos buscar si hay algún camino hamiltoniano en el gráfico. Si hay al menos una ruta, imprimimos una ruta; de lo contrario, imprimimos «Sin solución». 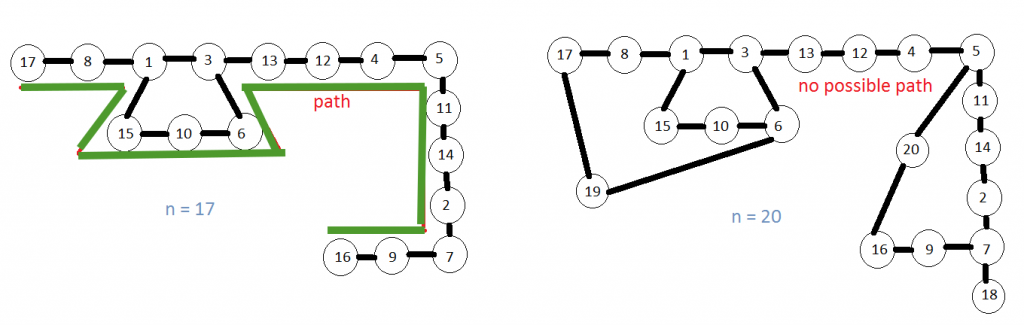 Acercarse:
Acercarse:
1. First list up all the perfect square numbers which we can get by adding two numbers. We can get at max (2*n-1). so we will take only the squares up to (2*n-1). 2. Take an adjacency matrix to represent the graph. 3. For each number from 1 to n find out numbers with which it can add upto a perfect square number. Fill respective cells of the adjacency matrix by 1. 4. Now find if there is any Hamiltonian path in the graph using backtracking as discussed earlier.
Python3
# Python3 program for Sum-square series using # hamiltonian path concept and backtracking # Function to check whether we can add number # v with the path in the position pos. def issafe(v, graph, path, pos): # if there is no edge between v and the # last element of the path formed so far # return false. if (graph[path[pos - 1]][v] == 0): return False # Otherwise if there is an edge between # v and last element of the path formed so # far, then check all the elements of the # path. If v is already in the path return # false. for i in range(pos): if (path[i] == v): return False # If none of the previous cases satisfies # then we can add v to the path in the # position pos. Hence return true. return True # Function to form a path based on the graph. def formpath(graph, path, pos): # If all the elements are included in the # path i.e. length of the path is n then # return true i.e. path formed. n = len(graph) - 1 if (pos == n + 1): return True # This loop checks for each element if it # can be fitted as the next element of the # path and recursively finds the next # element of the path. for v in range(1, n + 1): if issafe(v, graph, path, pos): path[pos] = v # Recurs for next element of the path. if (formpath(graph, path, pos + 1) == True): return True # If adding v does not give a solution # then remove it from path path[pos] = -1 # if any vertex cannot be added with the # formed path then return false and # backtracks. return False # Function to find out sum-square series. def hampath(n): # base case: if n = 1 there is no solution if n == 1: return 'No Solution' # Make an array of perfect squares from 1 # to (2 * n-1) l = list() for i in range(1, int((2 * n-1) ** 0.5) + 1): l.append(i**2) # Form the graph where sum of two adjacent # vertices is a perfect square graph = [[0 for i in range(n + 1)] for j in range(n + 1)] for i in range(1, n + 1): for ele in l: if ((ele-i) > 0 and (ele-i) <= n and (2 * i != ele)): graph[i][ele - i] = 1 graph[ele - i][i] = 1 # starting from 1 upto n check for each # element i if any path can be formed # after taking i as the first element. for j in range(1, n + 1): path = [-1 for k in range(n + 1)] path[1] = j # If starting from j we can form any path # then we will return the path if formpath(graph, path, 2) == True: return path[1:] # If no path can be formed at all return # no solution. return 'No Solution' # Driver Function print(17, '->', hampath(17)) print(20, '->', hampath(20)) print(25, '->', hampath(25))
17 -> [16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17] 20 -> No Solution 25 -> [2, 23, 13, 12, 24, 25, 11, 14, 22, 3, 1, 8, 17, 19, 6, 10, 15, 21, 4, 5, 20, 16, 9, 7, 18]
Producción:
17 -> [16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17]
20 -> No Solution
25 -> [2, 23, 13, 12, 24, 25, 11, 14, 22, 3, 1, 8, 17, 19, 6, 10,
15, 21, 4, 5, 20, 16, 9, 7, 18]
Discusión: este algoritmo de retroceso toma un tiempo exponencial para encontrar la ruta hamiltoniana. Por lo tanto, la complejidad temporal de este algoritmo es exponencial. En la última parte de la función hampath(n), si simplemente imprimimos la ruta en lugar de devolverla, imprimirá todas las rutas hamiltonianas posibles, es decir, todas las representaciones posibles. En realidad, primero obtendremos una representación como esta para n = 15. Para n<15 no hay representación. Para n = 18, 19, 20, 21, 22, 24 tampoco existe un camino hamiltoniano. Para el resto de los números funciona bien. Referencia: Numberphile