Permutaciones de n cosas tomadas r a la vez con k cosas juntas

Dados n, r y K. La tarea es encontrar el número de permutaciones de  cosas diferentes tomadas  a la vez de modo que  las cosas específicas siempre ocurran juntas.
Ejemplos: 
 

Input : n = 8, r = 5, k = 2
Output : 960

Input : n = 6, r = 2, k = 2
Output : 2

Acercarse: 
 

1. Un paquete de 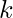 cosas específicas puede colocarse en r lugares de (r – k + 1) formas.
2. ¡k cosas específicas en el paquete se pueden organizar en k! maneras.
3. Ahora (n – k) las cosas se arreglarán en (r – k) lugares de 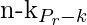 maneras.

Así, usando el principio fundamental de contar, el número requerido de permutaciones será: 
 

A continuación se muestra la implementación del enfoque anterior: 
 

// CPP program to find the number of permutations of
// n different things taken r at a time
// with k things grouped together
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find factorial
// of a number
int factorial(int n)
{
    int fact = 1;
 
    for (int i = 2; i <= n; i++)
        fact = fact * i;
 
    return fact;
}
 
// Function to calculate p(n, r)
int npr(int n, int r)
{
    int pnr = factorial(n) / factorial(n - r);
 
    return pnr;
}
 
// Function to find the number of permutations of
// n different things taken r at a time
// with k things grouped together
int countPermutations(int n, int r, int k)
{
    return factorial(k) * (r - k + 1) * npr(n - k, r - k);
}
 
// Driver code
int main()
{
    int n = 8;
    int r = 5;
    int k = 2;
 
    cout << countPermutations(n, r, k);
 
    return 0;
}

// Java program to find the number of permutations of
// n different things taken r at a time
// with k things grouped together
 
class GFG{
// Function to find factorial
// of a number
static int factorial(int n)
{
    int fact = 1;
 
    for (int i = 2; i <= n; i++)
        fact = fact * i;
 
    return fact;
}
 
// Function to calculate p(n, r)
static int npr(int n, int r)
{
    int pnr = factorial(n) / factorial(n - r);
 
    return pnr;
}
 
// Function to find the number of permutations of
// n different things taken r at a time
// with k things grouped together
static int countPermutations(int n, int r, int k)
{
    return factorial(k) * (r - k + 1) * npr(n - k, r - k);
}
 
// Driver code
public static void main(String[] args)
{
    int n = 8;
    int r = 5;
    int k = 2;
 
    System.out.println(countPermutations(n, r, k));
}
}
// this code is contributed by mits

# Python3 program to find the number of permutations of
# n different things taken r at a time
# with k things grouped together
 
# def to find factorial
# of a number
def factorial(n):
  
    fact = 1;
 
    for i in range(2,n+1):
        fact = fact * i;
 
    return fact;
  
 
# def to calculate p(n, r)
def npr(n, r):
  
    pnr = factorial(n) / factorial(n - r);
 
    return pnr;
  
 
# def to find the number of permutations of
# n different things taken r at a time
# with k things grouped together
def countPermutations(n, r, k):
  
    return int(factorial(k) * (r - k + 1) * npr(n - k, r - k));
  
 
# Driver code
n = 8;
r = 5;
k = 2;
 
print(countPermutations(n, r, k));
     
# this code is contributed by mits

// C# program to find the number of
// permutations of n different things
// taken r at a time with k things
// grouped together
using System;
 
class GFG
{
     
// Function to find factorial
// of a number
static int factorial(int n)
{
    int fact = 1;
 
    for (int i = 2; i <= n; i++)
        fact = fact * i;
 
    return fact;
}
 
// Function to calculate p(n, r)
static int npr(int n, int r)
{
    int pnr = factorial(n) /
              factorial(n - r);
 
    return pnr;
}
 
// Function to find the number of
// permutations of n different
// things taken r at a time with
// k things grouped together
static int countPermutations(int n,
                             int r, int k)
{
    return factorial(k) * (r - k + 1) *
                    npr(n - k, r - k);
}
 
// Driver code
static void Main()
{
    int n = 8;
    int r = 5;
    int k = 2;
 
    Console.WriteLine(countPermutations(n, r, k));
}
}
 
// This code is contributed by mits

<?php
// PHP program to find the number
// of permutations of n different
// things taken r at a time
// with k things grouped together
 
// Function to find factorial
// of a number
function factorial($n)
{
    $fact = 1;
 
    for ($i = 2; $i <= $n; $i++)
        $fact = $fact * $i;
 
    return $fact;
}
 
// Function to calculate p(n, r)
function npr($n, $r)
{
    $pnr = factorial($n) /
           factorial($n - $r);
 
    return $pnr;
}
 
// Function to find the number of
// permutations of n different
// things taken r at a time
// with k things grouped together
function countPermutations($n, $r, $k)
{
    return factorial($k) * ($r - $k + 1) *
                   npr($n - $k, $r - $k);
}
 
// Driver code
$n = 8;
$r = 5;
$k = 2;
 
echo countPermutations($n, $r, $k);
 
// This code is contributed by mits
?>

<script>
 
// JavaScript program to find the number of permutations of
// n different things taken r at a time
// with k things grouped together
 
// Function to find factorial
// of a number
function factorial(n)
{
    let fact = 1;
 
    for (let i = 2; i <= n; i++)
        fact = fact * i;
 
    return fact;
}
 
// Function to calculate p(n, r)
function npr(n, r)
{
    let pnr = Math.floor(factorial(n) / factorial(n - r));
 
    return pnr;
}
 
// Function to find the number of permutations of
// n different things taken r at a time
// with k things grouped together
 
function countPermutations(n, r, k)
{
    return factorial(k) * (r - k + 1) * npr(n - k, r - k);
}
 
// Driver code
    let n = 8;
    let r = 5;
    let k = 2;
 
    document.write(countPermutations(n, r, k));
 
// This code is contributed by Surbhi Tyagi.
 
</script>

960