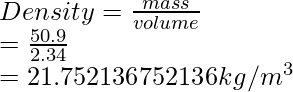Personajes importantes – Part 1

Para encontrar el valor de diferentes tamaños y compararlos, se utiliza la medición. Medir cosas no es solo un concepto, sino que también se usa prácticamente en la vida cotidiana, por ejemplo, un lechero mide la leche antes de venderla para asegurarse de que se sirve la cantidad correcta, Un sastre siempre mide el tamaño del cuerpo antes de hacer un traje, A el zapatero mide el tamaño del pie antes de hacer/dar la suela a los zapatos, y muchos otros ejemplos están disponibles a nuestro alrededor para demostrar la importancia de la medición.

Medición

La medición es comparar la cantidad a medir con la cantidad estándar disponible. La medición es un tema que no solo se enseña en matemáticas sino también en física y química, ya que cada materia requiere la comprensión de la medición para poder medir las cantidades.

Medir una cantidad no siempre da una respuesta perfectamente precisa. Solo los instrumentos de medición Ideal pueden proporcionar una respuesta perfectamente precisa. Prácticamente, la medición conduce a dos partes de una respuesta llamadas dígitos confiables y dígitos inciertos. 

Personajes importantes

Las Cifras Significativas o Dígitos Significativos se definen como los números que contienen todas las cifras ciertas y la primera cifra incierta. Por ejemplo, la longitud de un objeto se mide como 123,5 m, aquí 1, 2 y 3 son ciertos dígitos y 5 es el dígito incierto, por lo tanto, los dígitos significativos son 4 en este caso.

Si el valor de una cantidad tiene más de los dígitos significativos asignados al valor, es seguro que el valor de la cantidad será erróneo y engañoso. Esta es la razón por la que se enseñan los errores. Las cifras significativas se conocen como la resolución de la medida.

Reglas para determinar Cifras Significativas:

• Todos los dígitos distintos de cero se consideran cifras significativas.

 Por ejemplo, 67812 tiene 5 cifras significativas.

• Todos los ceros que se encuentran entre dos dígitos distintos de cero también se consideran significativos independientemente de la posición decimal en el valor.

 Por ejemplo, 1.03 tiene 3 cifras significativas.

• Si los ceros están presentes en el extremo derecho de un valor que no es un valor decimal, los ceros no se considerarán cifras significativas.

 Por ejemplo, 25000 tiene 2 cifras significativas. 

• Si el dígito es menor que 1, se deben notar dos cosas aquí. Primero, los ceros presentes al final del valor no se consideran cifras significativas. En segundo lugar, los ceros a la izquierda de los dígitos distintos de cero se consideran significativos.

 Por ejemplo, 0.067 (aquí 2 ceros están presentes en el lado izquierdo, se consideran de naturaleza significativa)

• Si el valor es de naturaleza decimal, los ceros finales se consideran cifras significativas.

 Por ejemplo, 2.30 tiene 3 cifras significativas.

Reglas al aplicar operaciones aritméticas en cifras significativas:

Dos valores cuando van de operación aritmética, el valor final obtenido siempre tendrá más cifras significativas obtenidas. Digamos que para determinar la corriente en un circuito, la resistencia y el voltaje se dan como 6,77 ohmios y 12,559 voltios. La corriente obtenida será 1.8550960118168, el valor de corriente tiene cifras mucho más significativas en comparación con los valores de voltaje y resistencia, pero se sabe que cuando se hace alguna operación sobre dos cantidades que contienen errores, el resultado final seguramente será más errores que las cantidades dadas. Por lo tanto, se establecen ciertas reglas para entender las cifras significativas cuando se someten a cualquier operación aritmética,

• Al dividir o multiplicar, el valor final obtenido debe tener la misma cantidad de cifras significativas que la cantidad en el valor de entrada (el valor de entrada con cifras menos significativas).

Por ejemplo, tome el ejemplo anterior donde R = 6,77 ohmios y V = 12,559 voltios, la corriente se describe como,

Yo = V/R

I = 12.559/6.77

yo = 1,850960118168 amperios

De acuerdo con la regla, I debe tener 3 dígitos significativos, es decir, I= 1,85 amperios.

• Al sumar o restar, el resultado final obtenido debe tener tantas cifras significativas como estén presentes en el valor de entrada con las cifras menos significativas.

Por ejemplo, tome entradas como 4.556 y 7.9864. Si se hace la suma en estas dos entradas, el resultado es 12.5424. Sin embargo, el resultado debe considerarse como 12.54.

Puntos importantes a tener en cuenta al determinar cifras significativas:

• El cambio en la unidad de un valor no cambiará el dígito significativo.

Por ejemplo: 23m = 2300cm = 230000 mm, Todos tienen 2 dígitos significativos.

• Es mejor usar notación científica al denotar medidas. La notación debe ser a × 10 ^b .

Por ejemplo, tome el ejemplo anterior, 23m = 2,3 × 10 ¹ m = 2,3 × 10 ³ cm = 2,3 × 10 ⁵ mm. En todo caso, la cifra significativa resultará ser 2.

• Si el dígito exacto se divide o multiplica, dará infinitos dígitos significativos.

Ejemplos de preguntas

Pregunta 1: Determine las cifras significativas en las siguientes cantidades,

1. 232
2. 1.500
3. 0.0899
4. 5,6 × 10 ³
5. 85633.98

Responder:

Con base en las reglas previstas para la determinación de dígitos significativos, 

1. 232= 3 cifras significativas
2. 1.500= 2 cifras significativas
3. 0.0899= 5 cifras significativas
4. 5.6 × 103 = 2 Cifras significativas
5. 85633.98 = 7 Cifras significativas.

Pregunta 2: Se suman dos dígitos, 33. 689 y 44. 23. Encuentre las cifras significativas en el valor resultante obtenido.

Responder:

Sumando 33,689 y 44,23, esto dará 77,919. Pero el valor de entrada con el dígito menos significativo es 44. 23. Por lo tanto, la respuesta es 77.91.

Pregunta 3: La masa de un objeto es de 50,9 kg y el volumen es de 2,34 m ³ . Encuentre la densidad del objeto con base en la regla de la cifra significativa.

Solución:

La densidad de un objeto se define como,

Ya que, el valor menos significativo en la entrada es 3.

Por lo tanto, la densidad del objeto es 21,7 kg/m ³ .

Pregunta 4: Se multiplican dos valores para obtener como resultado un valor determinado. Los valores de entrada son 3.99 y 1.5789, encuentre los dígitos significativos del valor resultante obtenido.

Responder:

Ni siquiera es necesario sumar los valores de entrada para encontrar la cifra significativa del valor resultante, ya que hay una manera más fácil. Con solo mirar las reglas, se puede ver que la primera regla de operaciones aritméticas de cifras significativas dice que el valor resultante tiene los mismos dígitos significativos que se encuentran en la entrada con el dígito menos significativo.

Por lo tanto, el resultado tendrá 3 dígitos significativos.

Pregunta 5: ¿Cuál es la diferencia entre 0,06700 y 6,700?

Responder:

La diferencia se debe al hecho de que 0,06700 es un número menor que 1 y, por lo tanto, los ceros de la izquierda son significativos, pero los ceros del extremo derecho son insignificantes (regla 4). Los dígitos significativos son 4.

Mientras que, el número 6.700 es un número mayor que 1 y también un decimal, por lo tanto, los ceros del lado derecho son significativos (regla 5). Los dígitos significativos son 4.