¿Por qué quicksort es mejor que mergesort?

Esta es una pregunta común que se hace en las entrevistas de DS que, a pesar del mejor rendimiento en el peor de los casos de mergesort, quicksort se considera mejor que mergesort . Hay ciertas razones por las cuales Quicksort es mejor, especialmente en el caso de arrays: 

1. Espacio auxiliar: Mergesort usa espacio adicional, quicksort requiere poco espacio y exhibe una buena localidad de caché. La clasificación rápida es un algoritmo de clasificación en el lugar. La clasificación en el lugar significa que no se necesita espacio de almacenamiento adicional para realizar la clasificación. La ordenación combinada requiere una array temporal para combinar las arrays ordenadas y, por lo tanto, no está en su lugar, lo que le da a la clasificación rápida la ventaja del espacio.
2. Peores casos: el peor caso de ordenación rápida O(n ² ) se puede evitar utilizando la ordenación rápida aleatoria. Se puede evitar fácilmente con una alta probabilidad eligiendo el pivote correcto. Obtener un comportamiento de caso promedio al elegir el elemento de pivote derecho hace que se improvise el rendimiento y se vuelva tan eficiente como la ordenación por combinación.
3. Localidad de referencia: Quicksort en particular exhibe una buena localidad de caché y esto lo hace más rápido que la ordenación por fusión en muchos casos, como en el entorno de memoria virtual.
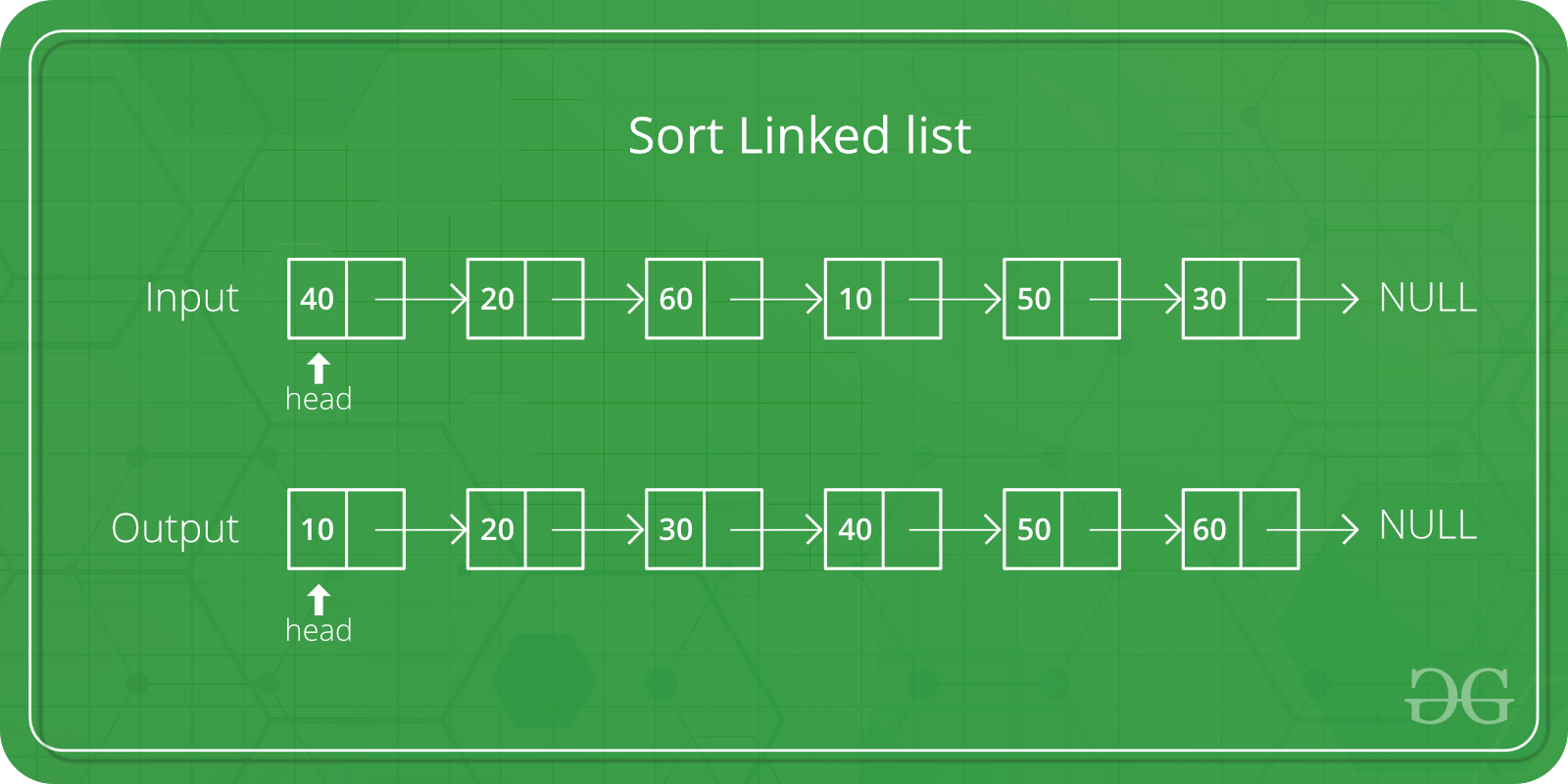
4. Merge sort es mejor para grandes estructuras de datos: Mergesort es una clasificación estable, a diferencia de quicksort y heapsort, y se puede adaptar fácilmente para operar en listas vinculadas y listas muy grandes almacenadas en medios de acceso lento, como almacenamiento en disco o almacenamiento conectado a la red. . Consulte esto para más detalles

La función std::sort() que está presente en C++ STL es un algoritmo de clasificación híbrido que proporciona una complejidad de tiempo promedio y en el peor de los casos de O(nlogn) . El algoritmo de clasificación que utiliza se llama Introsort. 

Introsort es una combinación de quicksort y heapsort. Comienza con quicksort y cambia a heapsort si la profundidad de recursión excede un nivel basado en la cantidad de elementos que se ordenan. 

Artículo relacionado: ¿Por qué se prefiere la ordenación rápida para arrays y la ordenación combinada para listas vinculadas? 

Este artículo es una contribución de Mandeep Singh . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. 

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.