Dado un conjunto de strings, encuentre el prefijo común más largo.
Ejemplos:
Input : {“geeksforgeeks”, “geeks”, “geek”, “geezer”}
Output : "gee"
Input : {"apple", "ape", "april"}
Output : "ap"
Hemos discutido los algoritmos de coincidencia palabra por palabra y carácter por carácter .
En este algoritmo, se analiza un enfoque de divide y vencerás. Primero dividimos las arrays de cuerdas en dos partes. Luego hacemos lo mismo para la parte izquierda y luego para la parte derecha. Lo haremos hasta ya menos que todas las strings tengan una longitud de 1. Ahora, después de eso, comenzaremos a conquistar devolviendo el prefijo común de las strings izquierda y derecha.
El algoritmo será claro usando la siguiente ilustración. Consideramos nuestras strings como – «geeksforgeeks», «geeks», «geek», «geezer».
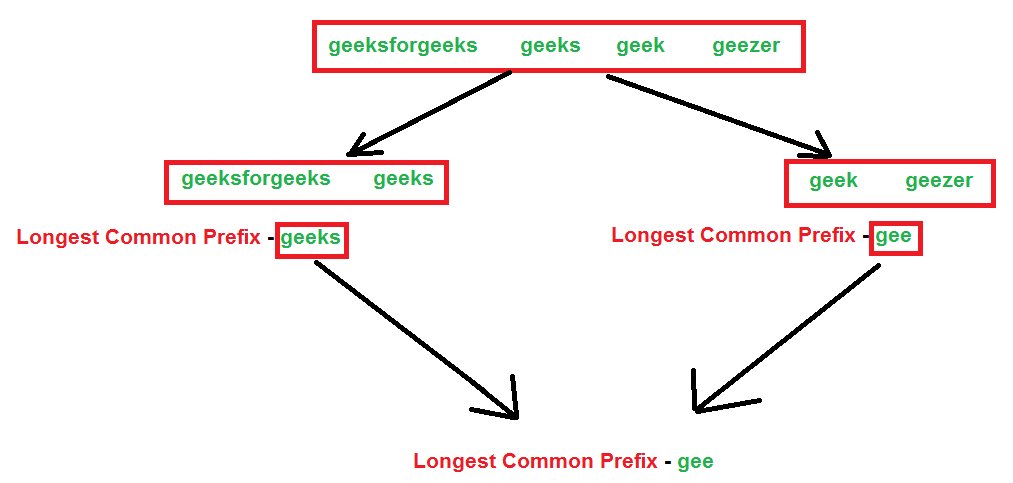
A continuación se muestra la implementación.
C++
// A C++ Program to find the longest common prefix
#include<bits/stdc++.h>
using namespace std;
// A Utility Function to find the common prefix between
// strings- str1 and str2
string commonPrefixUtil(string str1, string str2)
{
string result;
int n1 = str1.length(), n2 = str2.length();
for (int i=0, j=0; i<=n1-1&&j<=n2-1; i++,j++)
{
if (str1[i] != str2[j])
break;
result.push_back(str1[i]);
}
return (result);
}
// A Divide and Conquer based function to find the
// longest common prefix. This is similar to the
// merge sort technique
string commonPrefix(string arr[], int low, int high)
{
if (low == high)
return (arr[low]);
if (high > low)
{
// Same as (low + high)/2, but avoids overflow for
// large low and high
int mid = low + (high - low) / 2;
string str1 = commonPrefix(arr, low, mid);
string str2 = commonPrefix(arr, mid+1, high);
return (commonPrefixUtil(str1, str2));
}
}
// Driver program to test above function
int main()
{
string arr[] = {"geeksforgeeks", "geeks",
"geek", "geezer"};
int n = sizeof (arr) / sizeof (arr[0]);
string ans = commonPrefix(arr, 0, n-1);
if (ans.length())
cout << "The longest common prefix is "
<< ans;
else
cout << "There is no common prefix";
return (0);
}
Java
// Java Program to find the longest common prefix
class GFG {
// A Utility Function to find the common prefix between
// strings- str1 and str2
static String commonPrefixUtil(String str1, String str2) {
String result = "";
int n1 = str1.length(), n2 = str2.length();
for (int i = 0, j = 0; i <= n1 - 1 &&
j <= n2 - 1; i++, j++) {
if (str1.charAt(i) != str2.charAt(j)) {
break;
}
result += str1.charAt(i);
}
return (result);
}
// A Divide and Conquer based function to find the
// longest common prefix. This is similar to the
// merge sort technique
static String commonPrefix(String arr[], int low, int high) {
if (low == high) {
return (arr[low]);
}
if (high > low) {
// Same as (low + high)/2, but avoids overflow for
// large low and high
int mid = low + (high - low) / 2;
String str1 = commonPrefix(arr, low, mid);
String str2 = commonPrefix(arr, mid + 1, high);
return (commonPrefixUtil(str1, str2));
}
return null;
}
// Driver program to test above function
public static void main(String[] args) {
String arr[] = {"geeksforgeeks", "geeks",
"geek", "geezer"};
int n = arr.length;
String ans = commonPrefix(arr, 0, n - 1);
if (ans.length() != 0) {
System.out.println("The longest common prefix is "
+ ans);
} else {
System.out.println("There is no common prefix");
}
}
}
/* This JAVA code is contributed by 29AjayKumar*/
Python3
# A Python3 Program to find the longest common prefix
# A Utility Function to find the common
# prefix between strings- str1 and str2
def commonPrefixUtil(str1, str2):
result = ""
n1, n2 = len(str1), len(str2)
i, j = 0, 0
while i <= n1 - 1 and j <= n2 - 1:
if str1[i] != str2[j]:
break
result += str1[i]
i, j = i + 1, j + 1
return result
# A Divide and Conquer based function to
# find the longest common prefix. This is
# similar to the merge sort technique
def commonPrefix(arr, low, high):
if low == high:
return arr[low]
if high > low:
# Same as (low + high)/2, but avoids
# overflow for large low and high
mid = low + (high - low) // 2
str1 = commonPrefix(arr, low, mid)
str2 = commonPrefix(arr, mid + 1, high)
return commonPrefixUtil(str1, str2)
# Driver Code
if __name__ == "__main__":
arr = ["geeksforgeeks", "geeks",
"geek", "geezer"]
n = len(arr)
ans = commonPrefix(arr, 0, n - 1)
if len(ans):
print("The longest common prefix is", ans)
else:
print("There is no common prefix")
# This code is contributed by Rituraj Jain
C#
// C# Program to find the longest
// common prefix
using System;
class GFG
{
// A Utility Function to find
// the common prefix between
// strings- str1 and str2
static string commonPrefixUtil(string str1,
string str2)
{
string result = "";
int n1 = str1.Length,
n2 = str2.Length;
for (int i = 0, j = 0;
i <= n1 - 1 && j <= n2 - 1;
i++, j++)
{
if (str1[i] != str2[j])
break;
result += str1[i];
}
return (result);
}
// A Divide and Conquer based
// function to find the longest
// common prefix. This is similar
// to the merge sort technique
static string commonPrefix(string []arr,
int low, int high)
{
if (low == high)
return (arr[low]);
if (high > low)
{
// Same as (low + high)/2,
// but avoids overflow for
// large low and high
int mid = low + (high - low) / 2;
string str1 = commonPrefix(arr, low, mid);
string str2 = commonPrefix(arr, mid + 1, high);
return (commonPrefixUtil(str1, str2));
}
return null;
}
// Driver Code
public static void Main()
{
String []arr = {"geeksforgeeks", "geeks",
"geek", "geezer"};
int n = arr.Length;
String ans = commonPrefix(arr, 0, n - 1);
if (ans.Length!= 0)
{
Console.Write("The longest common " +
"prefix is " + ans);
}
else
{
Console.Write("There is no common prefix");
}
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program to find the
// longest common prefix
// A Utility Function to find the
// common prefix between strings-
// str1 and str2
function commonPrefixUtil(str1, str2)
{
let result = "";
let n1 = str1.length, n2 = str2.length;
for(let i = 0, j = 0; i <= n1 - 1 &&
j <= n2 - 1; i++, j++)
{
if (str1[i] != str2[j])
{
break;
}
result += str1[i];
}
return (result);
}
// A Divide and Conquer based function
// to find the longest common prefix. This
// is similar to the merge sort technique
function commonPrefix(arr, low, high)
{
if (low == high)
{
return (arr[low]);
}
if (high > low)
{
// Same as (low + high)/2, but avoids
// overflow for large low and high
let mid = low + Math.floor((high - low) / 2);
let str1 = commonPrefix(arr, low, mid);
let str2 = commonPrefix(arr, mid + 1, high);
return (commonPrefixUtil(str1, str2));
}
return null;
}
// Driver code
let arr = [ "geeksforgeeks", "geeks",
"geek", "geezer" ];
let n = arr.length;
let ans = commonPrefix(arr, 0, n - 1);
if (ans.length != 0)
{
document.write(
"The longest common prefix is " + ans);
}
else
{
document.write(
"There is no common prefix");
}
// This code is contributed by rag2127
</script>
The longest common prefix is gee
Complejidad de tiempo: dado que estamos iterando a través de todos los caracteres de todas las strings, podemos decir que la complejidad de tiempo es O (NM) donde,
N = Number of strings M = Length of the largest string string
Espacio auxiliar: para almacenar la string de prefijo más larga, estamos asignando espacio que es O (M Log N).
Este artículo es una contribución de Rachit Belwariar . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA