Dado un conjunto de strings, encuentre el prefijo común más largo.
Input : {“geeksforgeeks”, “geeks”, “geek”, “geezer”}
Output : "gee"
Input : {"apple", "ape", "april"}
Output : "ap"
Hemos discutido el algoritmo de coincidencia palabra por palabra en una publicación anterior .
En este algoritmo, en lugar de pasar por las strings una por una, pasaremos por los caracteres uno por uno.
Consideramos nuestras strings como – «geeksforgeeks», «geeks», «geek», «geezer».

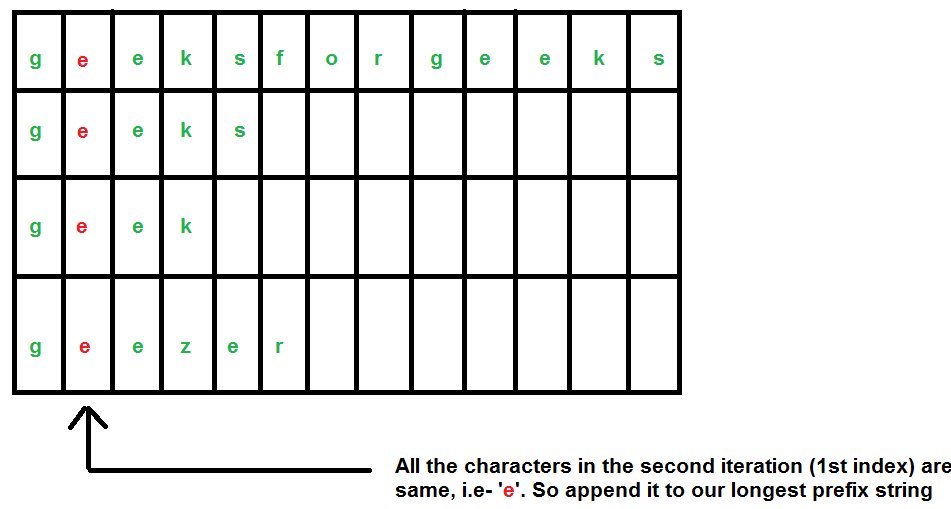


A continuación se muestra la implementación de este enfoque.
C++
// A C++ Program to find the longest common prefix
#include<bits/stdc++.h>
using namespace std;
// A Function to find the string having the minimum
// length and returns that length
int findMinLength(string arr[], int n)
{
int min = arr[0].length();
for (int i=1; i<n; i++)
if (arr[i].length() < min)
min = arr[i].length();
return(min);
}
// A Function that returns the longest common prefix
// from the array of strings
string commonPrefix(string arr[], int n)
{
int minlen = findMinLength(arr, n);
string result; // Our resultant string
char current; // The current character
for (int i=0; i<minlen; i++)
{
// Current character (must be same
// in all strings to be a part of
// result)
current = arr[0][i];
for (int j=1 ; j<n; j++)
if (arr[j][i] != current)
return result;
// Append to result
result.push_back(current);
}
return (result);
}
// Driver program to test above function
int main()
{
string arr[] = {"geeksforgeeks", "geeks",
"geek", "geezer"};
int n = sizeof (arr) / sizeof (arr[0]);
string ans = commonPrefix (arr, n);
if (ans.length())
cout << "The longest common prefix is "
<< ans;
else
cout << "There is no common prefix";
return (0);
}
Java
// A Java Program to find the longest common prefix
class GFG
{
// A Function to find the string having the minimum
// length and returns that length
static int findMinLength(String arr[], int n)
{
int min = arr[0].length();
for (int i = 1; i < n; i++)
{
if (arr[i].length() < min)
{
min = arr[i].length();
}
}
return (min);
}
// A Function that returns the longest common prefix
// from the array of strings
static String commonPrefix(String arr[], int n)
{
int minlen = findMinLength(arr, n);
String result = ""; // Our resultant string
char current; // The current character
for (int i = 0; i < minlen; i++)
{
// Current character (must be same
// in all strings to be a part of
// result)
current = arr[0].charAt(i);
for (int j = 1; j < n; j++)
{
if (arr[j].charAt(i) != current)
{
return result;
}
}
// Append to result
result += (current);
}
return (result);
}
// Driver program to test above function
public static void main(String[] args)
{
String arr[] = {"geeksforgeeks", "geeks",
"geek", "geezer"};
int n = arr.length;
String ans = commonPrefix(arr, n);
if (ans.length() > 0) {
System.out.println("The longest common prefix is "
+ ans);
} else {
System.out.println("There is no common prefix");
}
}
}
// This code contributed by Rajput-Ji
Python 3
# Python 3 Program to find the longest common prefix
# A Function to find the string having the minimum
# length and returns that length
def findMinLength(arr, n):
min = len(arr[0])
for i in range(1,n):
if (len(arr[i])< min):
min = len(arr[i])
return(min)
# A Function that returns the longest common prefix
# from the array of strings
def commonPrefix(arr, n):
minlen = findMinLength(arr, n)
result =""
for i in range(minlen):
# Current character (must be same
# in all strings to be a part of
# result)
current = arr[0][i]
for j in range(1,n):
if (arr[j][i] != current):
return result
# Append to result
result = result+current
return (result)
# Driver program to test above function
if __name__ == "__main__":
arr = ["geeksforgeeks", "geeks",
"geek", "geezer"]
n = len(arr)
ans = commonPrefix (arr, n)
if (len(ans)):
print("The longest common prefix is ",ans)
else:
print("There is no common prefix")
C#
// A C# Program to find the longest common prefix
using System;
class GFG
{
// A Function to find the string having the minimum
// length and returns that length
static int findMinLength(String []arr, int n)
{
int min = arr[0].Length;
for (int i = 1; i < n; i++)
{
if (arr[i].Length < min)
{
min = arr[i].Length;
}
}
return (min);
}
// A Function that returns the longest common prefix
// from the array of strings
static String commonPrefix(String []arr, int n)
{
int minlen = findMinLength(arr, n);
String result = ""; // Our resultant string
char current; // The current character
for (int i = 0; i < minlen; i++)
{
// Current character (must be same
// in all strings to be a part of
// result)
current = arr[0][i];
for (int j = 1; j < n; j++)
{
if (arr[j][i] != current)
{
return result;
}
}
// Append to result
result += (current);
}
return (result);
}
// Driver code
public static void Main(String[] args)
{
String []arr = {"geeksforgeeks", "geeks",
"geek", "geezer"};
int n = arr.Length;
String ans = commonPrefix(arr, n);
if (ans.Length > 0)
{
Console.WriteLine("The longest common prefix is "
+ ans);
}
else
{
Console.WriteLine("There is no common prefix");
}
}
}
/* This code contributed by PrinciRaj1992 */
Javascript
<script>
// A Javascript Program to find the longest common prefix
// A Function to find the string having the minimum
// length and returns that length
function findMinLength(arr,n)
{
let min = arr[0].length;
for (let i = 1; i < n; i++)
{
if (arr[i].length < min)
{
min = arr[i].length;
}
}
return (min);
}
// A Function that returns the longest common prefix
// from the array of strings
function commonPrefix(arr,n)
{
let minlen = findMinLength(arr, n);
let result = ""; // Our resultant string
let current; // The current character
for (let i = 0; i < minlen; i++)
{
// Current character (must be same
// in all strings to be a part of
// result)
current = arr[0][i];
for (let j = 1; j < n; j++)
{
if (arr[j][i] != current)
{
return result;
}
}
// Append to result
result += (current);
}
return (result);
}
// Driver program to test above function
let arr=["geeksforgeeks", "geeks",
"geek", "geezer"]
let n = arr.length;
let ans = commonPrefix(arr, n);
if (ans.length > 0) {
document.write("The longest common prefix is "
+ ans);
} else {
document.write("There is no common prefix");
}
// This code is contributed by avanitrachhadiya2155
</script>
The longest common prefix is gee
¿Cómo es este algoritmo mejor que el algoritmo » Coincidencia palabra por palabra «?
En el Conjunto 1 discutimos sobre el algoritmo de «coincidencia palabra por palabra».
Suponga que tiene las strings de entrada como: «geeksforgeeks», «geeks», «geek», «geezer», «x».
Ahora no hay una string de prefijo común de las strings anteriores. Mediante el algoritmo de «coincidencia palabra por palabra» discutido en el Conjunto 1, llegamos a la conclusión de que no hay una string de prefijo común al atravesar todas las strings. Pero si usamos este algoritmo, entonces en la primera iteración nos daremos cuenta de que no hay una string de prefijo común, ya que no vamos más allá para buscar el segundo carácter de cada string.
Este algoritmo tiene una gran ventaja cuando hay demasiadas strings.
Complejidad de tiempo: dado que estamos iterando a través de todos los caracteres de todas las strings, podemos decir que la complejidad de tiempo es O (NM) donde,
N = Number of strings M = Length of the Smallest string
Espacio auxiliar: para almacenar la string de prefijos más larga, estamos asignando un espacio que es O (M).
Método 3 (usando alguna función STL de C++ incorporada):
En este enfoque, en primer lugar, encontraremos la string con la longitud más pequeña. Luego buscaremos en todas las demás strings si esta string más pequeña está presente como prefijo o no. Si en todas las strings está presente esta pequeña string, imprimiremos esta string; de lo contrario, seguiremos reduciendo la longitud de la string más pequeña en uno hasta que su longitud sea cero.
A continuación se muestra la implementación del enfoque anterior:
Implementación:
C++
// C++ program to find the longest common
// prefix.
#include <bits/stdc++.h>
using namespace std;
// function to find the smallest string
// among all string
int shortest_string(string s[], int n)
{
int minlength = INT_MAX, min_index;
for (int i = 0; i < n; i++) {
if (s[i].length() < minlength) {
minlength = s[i].length();
min_index = i;
}
}
return min_index;
}
// function to find longest common
// prefix among all strings.
string findprefix(string s[], int n)
{
// index of the smallest string
int shortest_string_index = shortest_string(s, n);
while (s[shortest_string_index].length() > 0) {
int count = 0;
for (int i = 0; i < n; i++) {
// checking whether all strings have prefix
// which is equal to smallest string
if (s[i].find(s[shortest_string_index]) == 0) {
count++;
}
}
// checking that all the string's
// prefix is equal to smallest string
// or not.
if (count == n) {
cout << "longest common prefix is: " << endl;
return s[shortest_string_index];
break;
}
// deleting the last character
// of the smallest string.
s[shortest_string_index].pop_back();
}
return "no common prefix among all strings";
}
// driver code
int main()
{
string s[]
= { "geeksforgeeks", "geeks", "geek", "geezer" };
int n = sizeof(s) / sizeof(s[0]);
// function call
cout << findprefix(s, n);
return 0;
}
// this code is contributed by Machhaliya Mohammad.
longest common prefix is: gee
Complejidad de tiempo: O(n*m) donde n es el número total de strings y m es la longitud de la string más pequeña entre todas las strings.
Espacio auxiliar: O(1)
Este artículo es una contribución de Rachit Belwariar . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA