Preguntas de práctica sobre la codificación Huffman

La codificación Huffman es un tema importante desde el punto de vista de GATE y se hacen diferentes tipos de preguntas a partir de este tema. Antes de comprender este artículo, debe tener una idea básica sobre la codificación Huffman .

Estos son los tipos de preguntas que se hacen en GATE basado en la codificación Huffman.

Tipo 1. Preguntas conceptuales basadas en la Codificación Huffman.
Estos son algunos puntos clave basados ​​en la Codificación Huffman:

• Es una técnica de compresión de datos sin pérdidas que genera códigos de longitud variable para diferentes símbolos.
• Se basa en un enfoque codicioso que considera la frecuencia/probabilidad de los alfabetos para generar códigos.
• Tiene una complejidad de nlogn donde n es el número de caracteres únicos.
• La longitud del código de un carácter es inversamente proporcional a la frecuencia de su aparición.
• Ningún código es prefijo de otro código debido al cual una secuencia de código puede decodificarse sin ambigüedades en caracteres.

Que – 1. ¿Cuál de los siguientes es cierto acerca de la codificación Huffman?
(A) La codificación Huffman puede tener pérdidas en algunos casos
(B) Los códigos Huffman pueden no ser códigos sin pérdidas óptimos en algunos casos
(C) En la codificación Huffman, ningún código es prefijo de ningún otro código.
(Todo lo anterior

Solución: como se mencionó, la codificación Huffman es una técnica de compresión sin pérdidas. Por lo tanto, las opciones (A) y (B) son falsas. La opción (C) es verdadera ya que esta es la base de la decodificación del mensaje del código dado.

Tipo 2. Para encontrar el número de bits para codificar un mensaje dado.
Para resolver este tipo de preguntas:

• Primero calcule la frecuencia de los caracteres si no se proporciona
• Generar árbol de Huffman
• Calcule la cantidad de bits utilizando la frecuencia de los caracteres y la cantidad de bits necesarios para representar esos caracteres.

Que – 2. ¿Cuántos bits pueden ser necesarios para codificar el mensaje ‘mississippi’?

Solución: La siguiente es la tabla de frecuencia de caracteres en ‘mississippi’ en orden de frecuencia no decreciente:

El árbol de Huffman generado es: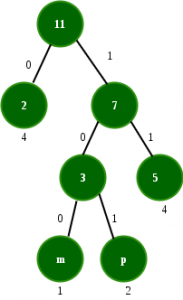

Los siguientes son los códigos: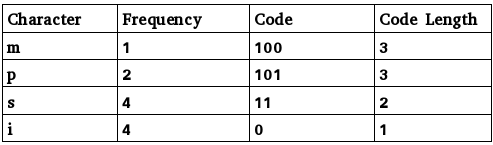

Número total de bits
= frecuencia (m) * longitud de código (m) + frecuencia (p) * longitud de código (p) + frecuencia (s) * longitud de código (s) + frecuencia (i) * longitud de código (i)
= 1*3 + 2*3 + 4*2 + 4*1 = 21

Además, el promedio de bits por carácter se puede encontrar como:
Número total de bits requeridos / número total de caracteres = 21/11 = 1,909

Tipo 3. Decodificación de código a mensaje –
Para resolver este tipo de preguntas:

• Genere códigos para cada personaje usando el árbol de Huffman (si no se proporciona)
• Usando la coincidencia de prefijos, reemplace los códigos con caracteres.

Que – 3. Los caracteres de la a a la h tienen el conjunto de frecuencias basado en los primeros 8 números de Fibonacci de la siguiente manera:

a : 1, b : 1, c : 2, d : 3, e : 5, f : 8, g : 13, h : 21

Se utiliza un código Huffman para representar los caracteres. ¿Cuál es la secuencia de caracteres correspondiente al siguiente código?

110111100111010

(A) fdheg
(B) ecgdf
(C) dchfg
(D) fehdg

Solución: Usando las frecuencias dadas en la pregunta, el árbol de Huffman se puede generar como:

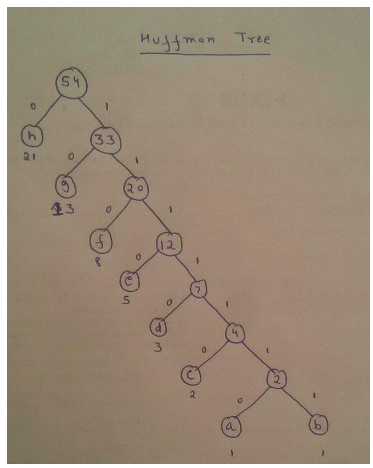
Los siguientes son los códigos:

Usando la coincidencia de prefijos, la string dada se puede descomponer como

110 11110 0 1110 10
f   d     h  e   g

Tipo 4. Número de bits guardados usando la codificación Huffman –

Que – 4. Una empresa de redes utiliza una técnica de compresión para codificar el mensaje antes de transmitirlo a través de la red. Supongamos que el mensaje contiene los siguientes caracteres con su frecuencia:

Tenga en cuenta que cada carácter en el mensaje de entrada ocupa 1 byte.

Si la técnica de compresión utilizada es Huffman Coding, ¿cuántos bits se guardarán en el mensaje?
(A) 224
(B) 800
(C) 576
(D) 324

Soluciones: Encontrar el número de bits sin usar Huffman,
Número total de caracteres = suma de frecuencias = 100
tamaño de 1 carácter = 1 byte = 8 bits
Número total de bits = 8*100 = 800

Usando la codificación Huffman, el número total de bits necesarios se puede calcular como:

5*4 + 9*4 + 12*3 + 13*3 + 16*3 + 45* 1 = 224

Bits guardados = 800-224 = 576.