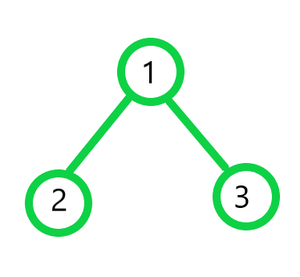
Dado un árbol binario , la tarea es imprimir todos los Nodes del árbol binario en Pre-order , Post-order y In-order iterativamente usando solo un recorrido de pila .
Ejemplos:
Aporte:
Salida:
Recorrido en orden previo : 1 2 3
Recorrido en orden: 2 1 3
Recorrido en orden posterior: 2 3 1Aporte:
Salida:
Recorrido en orden previo: 1 2 4 5 3 6 7
Recorrido en orden: 4 2 5 1 6 3 7 Recorrido
en orden posterior: 4 5 2 6 7 3 1
Enfoque: el problema se puede resolver usando solo una pila. La idea es marcar cada Node del árbol binario asignando un valor, llamado código de estado con cada Node, de modo que el valor 1 representa que el Node está visitando actualmente en orden de recorrido, el valor 2 representa los Nodes que está visitando actualmente en orden de recorrido y el valor 3 representa el Node que está visitando en el recorrido posterior al pedido.
- Inicialice una pila < par < Node*, int>> digamos S .
- Inserte el Node raíz en la pila con el estado 1 , es decir, {raíz, 1}.
- Inicialice tres vectores de números enteros , por ejemplo , preorder , inorder y postorder .
- Recorra la pila hasta que esté vacía y verifique las siguientes condiciones:
- Si el estado del Node superior de la pila es 1 , actualice el estado del Node superior de la pila a 2 y empuje el Node superior en el orden previo del vector e inserte el hijo izquierdo del Node superior si no es NULL en el pila s
- Si el estado del Node superior de la pila es 2 , actualice el estado del Node superior de la pila a 3 y empuje el Node superior en el vector en orden e inserte el hijo derecho del Node superior si no es NULL en el pila S. _
- Si el estado del Node superior de la pila es 3 , empuje el Node superior en orden posterior del vector y luego extraiga el elemento superior.
- Finalmente, imprima los vectores preorder , inorder y postorder .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Structure of the
// node of a binary tree
struct Node {
int data;
struct Node *left, *right;
Node(int data)
{
this->data = data;
left = right = NULL;
}
};
// Function to print all nodes of a
// binary tree in Preorder, Postorder
// and Inorder using only one stack
void allTraversal(Node* root)
{
// Stores preorder traversal
vector<int> pre;
// Stores inorder traversal
vector<int> post;
// Stores postorder traversal
vector<int> in;
// Stores the nodes and the order
// in which they are currently visited
stack<pair<Node*, int> > s;
// Push root node of the tree
// into the stack
s.push(make_pair(root, 1));
// Traverse the stack while
// the stack is not empty
while (!s.empty()) {
// Stores the top
// element of the stack
pair<Node*, int> p = s.top();
// If the status of top node
// of the stack is 1
if (p.second == 1) {
// Update the status
// of top node
s.top().second++;
// Insert the current node
// into preorder, pre[]
pre.push_back(p.first->data);
// If left child is not NULL
if (p.first->left) {
// Insert the left subtree
// with status code 1
s.push(make_pair(
p.first->left, 1));
}
}
// If the status of top node
// of the stack is 2
else if (p.second == 2) {
// Update the status
// of top node
s.top().second++;
// Insert the current node
// in inorder, in[]
in.push_back(p.first->data);
// If right child is not NULL
if (p.first->right) {
// Insert the right subtree into
// the stack with status code 1
s.push(make_pair(
p.first->right, 1));
}
}
// If the status of top node
// of the stack is 3
else {
// Push the current node
// in post[]
post.push_back(p.first->data);
// Pop the top node
s.pop();
}
}
cout << "Preorder Traversal: ";
for (int i = 0; i < pre.size(); i++) {
cout << pre[i] << " ";
}
cout << "\n";
// Printing Inorder
cout << "Inorder Traversal: ";
for (int i = 0; i < in.size(); i++) {
cout << in[i] << " ";
}
cout << "\n";
// Printing Postorder
cout << "Postorder Traversal: ";
for (int i = 0; i < post.size(); i++) {
cout << post[i] << " ";
}
cout << "\n";
}
// Driver Code
int main()
{
// Creating the root
struct Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);
// Function call
allTraversal(root);
return 0;
}
Java
// Java program for the above approach
import java.util.ArrayList;
import java.util.Stack;
class GFG
{
static class Pair
{
Node first;
int second;
public Pair(Node first, int second)
{
this.first = first;
this.second = second;
}
}
// Structure of the
// node of a binary tree
static class Node
{
int data;
Node left, right;
Node(int data)
{
this.data = data;
left = right = null;
}
};
// Function to print all nodes of a
// binary tree in Preorder, Postorder
// and Inorder using only one stack
static void allTraversal(Node root)
{
// Stores preorder traversal
ArrayList<Integer> pre = new ArrayList<>();
// Stores inorder traversal
ArrayList<Integer> in = new ArrayList<>();
// Stores postorder traversal
ArrayList<Integer> post = new ArrayList<>();
// Stores the nodes and the order
// in which they are currently visited
Stack<Pair> s = new Stack<>();
// Push root node of the tree
// into the stack
s.push(new Pair(root, 1));
// Traverse the stack while
// the stack is not empty
while (!s.empty())
{
// Stores the top
// element of the stack
Pair p = s.peek();
// If the status of top node
// of the stack is 1
if (p.second == 1)
{
// Update the status
// of top node
s.peek().second++;
// Insert the current node
// into preorder, pre[]
pre.add(p.first.data);
// If left child is not null
if (p.first.left != null)
{
// Insert the left subtree
// with status code 1
s.push(new Pair(p.first.left, 1));
}
}
// If the status of top node
// of the stack is 2
else if (p.second == 2) {
// Update the status
// of top node
s.peek().second++;
// Insert the current node
// in inorder, in[]
in.add(p.first.data);
// If right child is not null
if (p.first.right != null) {
// Insert the right subtree into
// the stack with status code 1
s.push(new Pair(p.first.right, 1));
}
}
// If the status of top node
// of the stack is 3
else {
// Push the current node
// in post[]
post.add(p.first.data);
// Pop the top node
s.pop();
}
}
System.out.print("Preorder Traversal: ");
for (int i : pre) {
System.out.print(i + " ");
}
System.out.println();
// Printing Inorder
System.out.print("Inorder Traversal: ");
for (int i : in) {
System.out.print(i + " ");
}
System.out.println();
// Printing Postorder
System.out.print("Postorder Traversal: ");
for (int i : post) {
System.out.print(i + " ");
}
System.out.println();
}
// Driver Code
public static void main(String[] args) {
// Creating the root
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
// Function call
allTraversal(root);
}
}
// This code is contributed by sanjeev255
Python3
# Python3 program for the above approach
# Structure of the
# node of a binary tree
class Node:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
# Function to print all nodes of a
# binary tree in Preorder, Postorder
# and Inorder using only one stack
def allTraversal(root):
# Stores preorder traversal
pre = []
# Stores inorder traversal
post = []
# Stores postorder traversal
inn = []
# Stores the nodes and the order
# in which they are currently visited
s = []
# Push root node of the tree
# into the stack
s.append([root, 1])
# Traverse the stack while
# the stack is not empty
while (len(s) > 0):
# Stores the top
# element of the stack
p = s[-1]
#del s[-1]
# If the status of top node
# of the stack is 1
if (p[1] == 1):
# Update the status
# of top node
s[-1][1] += 1
# Insert the current node
# into preorder, pre[]
pre.append(p[0].data)
# If left child is not NULL
if (p[0].left):
# Insert the left subtree
# with status code 1
s.append([p[0].left, 1])
# If the status of top node
# of the stack is 2
elif (p[1] == 2):
# Update the status
# of top node
s[-1][1] += 1
# Insert the current node
# in inorder, in[]
inn.append(p[0].data);
# If right child is not NULL
if (p[0].right):
# Insert the right subtree into
# the stack with status code 1
s.append([p[0].right, 1])
# If the status of top node
# of the stack is 3
else:
# Push the current node
# in post[]
post.append(p[0].data);
# Pop the top node
del s[-1]
print("Preorder Traversal: ",end=" ")
for i in pre:
print(i,end=" ")
print()
# Printing Inorder
print("Inorder Traversal: ",end=" ")
for i in inn:
print(i,end=" ")
print()
# Printing Postorder
print("Postorder Traversal: ",end=" ")
for i in post:
print(i,end=" ")
print()
# Driver Code
if __name__ == '__main__':
# Creating the root
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
# Function call
allTraversal(root)
# This code is contributed by mohit kumar 29.
C#
// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG {
// Class containing left and
// right child of current
// node and key value
class Node {
public int data;
public Node left, right;
public Node(int x)
{
data = x;
left = right = null;
}
}
// Function to print all nodes of a
// binary tree in Preorder, Postorder
// and Inorder using only one stack
static void allTraversal(Node root)
{
// Stores preorder traversal
List<int> pre = new List<int>();
// Stores inorder traversal
List<int> In = new List<int>();
// Stores postorder traversal
List<int> post = new List<int>();
// Stores the nodes and the order
// in which they are currently visited
Stack<Tuple<Node, int>> s = new Stack<Tuple<Node, int>>();
// Push root node of the tree
// into the stack
s.Push(new Tuple<Node, int>(root, 1));
// Traverse the stack while
// the stack is not empty
while (s.Count > 0)
{
// Stores the top
// element of the stack
Tuple<Node, int> p = s.Peek();
// If the status of top node
// of the stack is 1
if (p.Item2 == 1)
{
// Update the status
// of top node
Tuple<Node, int> temp = s.Peek();
temp = new Tuple<Node, int>(temp.Item1, temp.Item2 + 1);
s.Pop();
s.Push(temp);
// Insert the current node
// into preorder, pre[]
pre.Add(p.Item1.data);
// If left child is not null
if (p.Item1.left != null)
{
// Insert the left subtree
// with status code 1
s.Push(new Tuple<Node, int>(p.Item1.left, 1));
}
}
// If the status of top node
// of the stack is 2
else if (p.Item2 == 2) {
// Update the status
// of top node
Tuple<Node, int> temp = s.Peek();
temp = new Tuple<Node, int>(temp.Item1, temp.Item2 + 1);
s.Pop();
s.Push(temp);
// Insert the current node
// in inorder, in[]
In.Add(p.Item1.data);
// If right child is not null
if (p.Item1.right != null) {
// Insert the right subtree into
// the stack with status code 1
s.Push(new Tuple<Node, int>(p.Item1.right, 1));
}
}
// If the status of top node
// of the stack is 3
else {
// Push the current node
// in post[]
post.Add(p.Item1.data);
// Pop the top node
s.Pop();
}
}
Console.Write("Preorder Traversal: ");
foreach(int i in pre) {
Console.Write(i + " ");
}
Console.WriteLine();
// Printing Inorder
Console.Write("Inorder Traversal: ");
foreach(int i in In) {
Console.Write(i + " ");
}
Console.WriteLine();
// Printing Postorder
Console.Write("Postorder Traversal: ");
foreach(int i in post) {
Console.Write(i + " ");
}
Console.WriteLine();
}
static void Main() {
// Creating the root
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
// Function call
allTraversal(root);
}
}
// This code is contributed by suresh07.
Javascript
<script>
// Javascript program for the above approach
class Pair
{
constructor(first, second)
{
this.first = first;
this.second = second;
}
}
// Structure of the
// node of a binary tree
class Node
{
constructor(data)
{
this.data = data;
this.left = this.right = null;
}
}
// Function to print all nodes of a
// binary tree in Preorder, Postorder
// and Inorder using only one stack
function allTraversal(root)
{
// Stores preorder traversal
let pre = [];
// Stores inorder traversal
let In = [];
// Stores postorder traversal
let post = [];
// Stores the nodes and the order
// in which they are currently visited
let s = [];
// Push root node of the tree
// into the stack
s.push(new Pair(root, 1));
// Traverse the stack while
// the stack is not empty
while (s.length != 0)
{
// Stores the top
// element of the stack
let p = s[s.length - 1];
// If the status of top node
// of the stack is 1
if (p.second == 1)
{
// Update the status
// of top node
s[s.length - 1].second++;
// Insert the current node
// into preorder, pre[]
pre.push(p.first.data);
// If left child is not null
if (p.first.left != null)
{
// Insert the left subtree
// with status code 1
s.push(new Pair(p.first.left, 1));
}
}
// If the status of top node
// of the stack is 2
else if (p.second == 2)
{
// Update the status
// of top node
s[s.length - 1].second++;
// Insert the current node
// in inorder, in[]
In.push(p.first.data);
// If right child is not null
if (p.first.right != null)
{
// Insert the right subtree into
// the stack with status code 1
s.push(new Pair(p.first.right, 1));
}
}
// If the status of top node
// of the stack is 3
else
{
// Push the current node
// in post[]
post.push(p.first.data);
// Pop the top node
s.pop();
}
}
document.write("Preorder Traversal: ");
for(let i = 0; i < pre.length; i++)
{
document.write(pre[i] + " ");
}
document.write("<br>");
// Printing Inorder
document.write("Inorder Traversal: ");
for(let i = 0; i < In.length; i++)
{
document.write(In[i] + " ");
}
document.write("<br>");
// Printing Postorder
document.write("Postorder Traversal: ");
for(let i = 0; i < post.length; i++)
{
document.write(post[i] + " ");
}
document.write("<br>");
}
// Driver Code
// Creating the root
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
// Function call
allTraversal(root);
// This code is contributed by unknown2108
</script>
Preorder Traversal: 1 2 4 5 3 6 7 Inorder Traversal: 4 2 5 1 6 3 7 Postorder Traversal: 4 5 2 6 7 3 1
Complejidad temporal: O(N)
Espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por deepika_sharma y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA