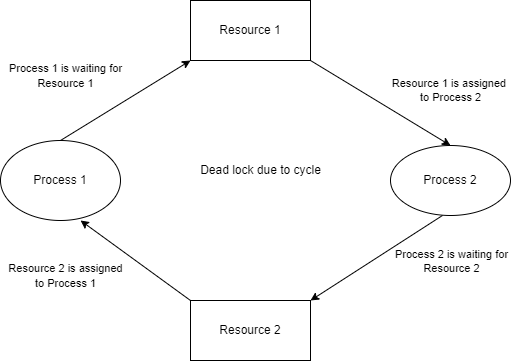
Los interbloqueos son los problemas fundamentales en los sistemas distribuidos. Un interbloqueo es una situación en la que se bloquea un conjunto de procesos, ya que cada proceso en un sistema distribuido tiene algunos recursos y otros procesos necesitan los recursos adquiridos. En esta situación, un ciclo llega a un punto muerto.
Condiciones de interbloqueo: Un proceso en sistemas distribuidos utiliza diferentes recursos de la siguiente manera.
- Solicitud
- Usar
- Lanzamientos
Eso significa que un proceso solicita el recurso y lo usa en su ejecución y después de la ejecución, libera el recurso.
Métodos para manejar el interbloqueo:
Hay cuatro métodos para manejar Deadlock:
- Prevención de interbloqueo
- Prevención de interbloqueos
- Detección de interbloqueo
- Recuperación de punto muerto
Prevención de interbloqueos:
En la prevención de bloqueos mutuos, se comprobará si el sistema se encuentra en un estado seguro o inseguro. El estado seguro se garantiza cuando se permite la solicitud del recurso por parte del proceso cuando no se encuentra ningún interbloqueo en el sistema. Si se encuentra un interbloqueo, el sistema estará en un estado inseguro.
Para evitar interbloqueos, el proceso debe informar al sistema cuántos recursos debe solicitar un proceso para su ejecución. Para que eso suceda, usamos Algorithm.
Paso 1: Trabajar y terminar los 2 vectores de tamaño m & n. Inicializar el trabajo con disponible y terminar[i] = falso
para i=1 a n, m=>#recursos y n=>#procesos.
Paso 2: encuentre una i tal que ambos (i) terminen [i] = falso (ii) necesiten (i) <= trabajo, si no existe tal i, vaya al Paso 4.
Paso 3: Trabajo = trabajo + asignación
terminar[i] = verdadero
vaya al Paso 2.
Paso 4: si finish[i] = true para todos los i , entonces el sistema está en un estado seguro.
Suponga que hay m = 4 (A, B, C, D) recursos y n = 5 (P0, P1, P2, P3, P4) procesos. Cree una secuencia segura para mantener el sistema en un estado seguro.

Aquí,
n => #processes = 5 = <P0, P1, P2, P3, P4> m => #resources = 4 = (A, B, C, D)
Disponible: Define cuántas instancias están disponibles para un recurso en particular. En el ejemplo anterior A – 1, B – 5, C – 2, D – 0 recursos disponibles.
Size = Available [m] => 1 D array.
Asignación: Define el número de instancias que se asignan para todos los recursos de un proceso en particular. En el ejemplo anterior para el Proceso P0, tenemos A – 0, B – 0, C – 1, D – 2 recursos asignados.
Size = Allocation [n x m] => 2 D array.
Max: Define el número máximo de instancias que están disponibles para todos los recursos de un proceso en particular. En el ejemplo anterior para el Proceso P0, tenemos un máximo de A – 0, B – 0, C – 1 y D – 2 recursos disponibles.
Size = Max [n x m] => 2 D array.
Necesidad: Indica cuantas instancias más se requerirán para un recurso de un proceso.
Size = Need [n x m] => 2 D array.
Para comprobar si hay una secuencia segura, primero tenemos que calcular la array de necesidad.
Need(i) = Max(i) - Allocation(i)
Por ejemplo, si tomamos P0 entonces la necesidad sería:
A = (0-0) B = (0-0) C = (1-1) D = (2-2) similarly for all processes.

Después de calcular la array de necesidades, ahora comience de acuerdo con el algoritmo.
Paso 1: Inicializar el trabajo y terminar

Paso 2: ahora tome el proceso P0 y, de acuerdo con el paso 2 del algoritmo, necesitamos encontrar una i tal que ambas condiciones
(i) finish[i] = false (ii) need(i) <= work should be satisfied. we found for P0, finish[i] = false and need(i) <= work
tal que 0<=1 -> Verdadero, 0<=5 -> Verdadero, 0<=2 -> Verdadero, 0<=0 -> Verdadero. Por lo que se cumplen ambas condiciones.
Ahora, de acuerdo con el paso 3 en el algoritmo, ejecute (trabajo = trabajo + asignación) y finalice [i] = verdadero y vaya al paso 2 en el algoritmo nuevamente.

Paso 3: Ahora tome el Proceso P1, encontramos terminar [i] = falso pero al llegar a necesitar (i) <= trabajo, la condición se volvió falsa
tal que 0<=1 -> Verdadero, 7<=5 -> Falso, 5<=3 -> Falso, 0<=2 -> Verdadero. La condición falló, así que omita el Proceso P1 y vaya al Proceso P2.
Paso 4: Para el Proceso P2, encontramos que se cumplen ambas condiciones. Entonces calcule de acuerdo con el paso 3 en el algoritmo.

Paso 5: Para el Proceso P3, encontramos que se cumplen ambas condiciones. Entonces calcule de acuerdo con el paso 3 en el algoritmo.

Paso 6: Para el Proceso P4, encontramos que se cumplen ambas condiciones. Entonces calcule de acuerdo con el paso 3 en el algoritmo.

Paso 7: Ahora nos quedamos con el Proceso P1. Entonces, si verificamos el Proceso P1, encontramos que ambas condiciones se cumplen. Entonces calcule de acuerdo con el paso 3 en el algoritmo.

Paso 8: Entonces, cuando volvamos al paso 2 en el algoritmo, no podemos encontrar ninguna ‘i’ para ambas condiciones, ya que todos los procesos se completaron. Así que ahora vaya al paso 4 en el algoritmo. encontramos todos terminar [i] = verdadero. Entonces, de acuerdo con el algoritmo, el sistema está en un estado seguro.
Finalmente, la secuencia segura para el ejemplo anterior sería <P0, P2, P3, P4, P1>.
Verificación cruzada : podemos verificar la solución agregando los valores de la array de asignación para cada recurso para todos los procesos con la array disponible para cada recurso, luego serían los valores finales de la array de trabajo para cada recurso.
En el ejemplo anterior si añadimos
=> Allocation + Available for resource 'A' for all processes = 0 + 1 + 1 + 0 + 0 + 1 = 3. => Allocation + Available for resource 'B' for all processes = 0 + 0 + 3 + 6 + 0 + 5 = 14. => Allocation + Available for resource 'C' for all processes = 1 + 0 + 5 + 3 + 1 + 2 = 12. => Allocation + Available for resource 'D' for all processes = 2 + 0 + 4 + 2 + 4 + 0 = 12.
Aquí, podemos observar claramente que los valores generados después de agregar los valores de la array Asignación y Disponible son iguales a los finales. Valores de la array de trabajo. Entonces el sistema está en un estado seguro.
Desventaja:
- Tiene un número fijo de procesos y recursos que se requieren durante la ejecución.
- No se pueden ejecutar otros procesos en el medio y tampoco se puede asignar ningún recurso a otro proceso hasta que llegue el punto muerto.
- Los recursos máximos que se adquieren para los procesos deben conocerse y asignarse con anticipación.
- En el algoritmo del banquero, todos los recursos se pueden solicitar durante un tiempo determinado, pero el tiempo es de un año.
- Entonces, estos procesos que están adquiriendo recursos pueden liberar esos recursos después de cierto período de tiempo, hasta entonces, los procesos restantes deben esperar la adquisición de recursos. Este es el problema del hambre.
Publicación traducida automáticamente
Artículo escrito por devasishakula503 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA