Probabilidad de obtener al menos K caras en N lanzamientos de monedas

Posted on by Rudeus Greyrat

Dado un número N de monedas, la tarea es encontrar la probabilidad de obtener al menos un número K de caras después de lanzar todas las N monedas simultáneamente.
Ejemplo : 
 

Suppose we have 3 unbiased coins and we have to
find the probability of getting at least 2 heads,
so there are 23 = 8 ways to toss these
coins, i.e.,
HHH, HHT, HTH, HTT, THH, THT, TTH, TTT 

Out of which there are 4 set which contain at
least 2 Heads i.e.,
HHH, HHT, HH, THH

So the probability is 4/8 or 0.5

La probabilidad de éxito exactamente k en n pruebas con probabilidad p de éxito en cualquier prueba viene dada por: 
{\displaystyle \binom{n}{k}p^k(1-p)^{n-k}=^{n}\textrm{c}_{k}(p)^k (1-p)^{n-k}=\frac {n!(p)^k (1-p)^{n-k}}{(k)!(n-k)!}}
Entonces, probabilidad (obtener al menos 4 caras) =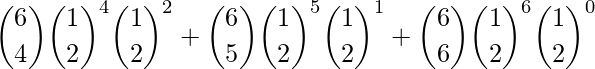  
{\displaystyle \binom{6}{4}\binom{1}{2}^4\binom{1}{2}^2+\binom{6}{5}\binom{1}{2}^5\binom{1}{2}^1+\binom{6}{6}\binom{1}{2}^6\binom{1}{2}^0}
{\displaystyle =\frac {1}{2^6} \left ( \frac {6!}{4!2!}+ \frac {6!}{5!1!}+ \frac {6!}{6!0!}\right )}
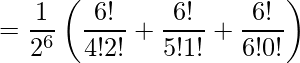
​​Método 1 (Ingenuo) 
Un enfoque Ingenuo es almacenar el valor del factorial en dp[] array y llamarlo directamente cuando sea necesario. Pero el problema de este enfoque es que solo podemos almacenarlo hasta cierto valor, después de eso conducirá a un desbordamiento.
A continuación se muestra la implementación del enfoque anterior. 
 

C++

// Naive approach in C++ to find probability of
// at least k heads
#include<bits/stdc++.h>
using namespace std;
#define MAX 21
 
double fact[MAX];
 
// Returns probability of getting at least k
// heads in n tosses.
double probability(int k, int n)
{
    double ans = 0;
    for (int i = k; i <= n; ++i)
 
        // Probability of getting exactly i
        // heads out of n heads
        ans += fact[n] / (fact[i] * fact[n - i]);
 
    // Note: 1 << n = pow(2, n)
    ans = ans / (1LL << n);
    return ans;
}
 
void precompute()
{
    // Preprocess all factorial only upto 19,
    // as after that it will overflow
    fact[0] = fact[1] = 1;
 
    for (int i = 2; i < 20; ++i)
        fact[i] = fact[i - 1] * i;
}
 
// Driver code
int main()
{
    precompute();
 
    // Probability of getting 2 head out of 3 coins
    cout << probability(2, 3) << "\n";
 
    // Probability of getting 3 head out of 6 coins
    cout << probability(3, 6) <<"\n";
 
    // Probability of getting 12 head out of 18 coins
    cout << probability(12, 18);
 
    return 0;
}

Java

// JAVA Code for Probability of getting
// atleast K heads in N tosses of Coins
class GFG {
     
    public static double fact[];
      
    // Returns probability of getting at least k
    // heads in n tosses.
    public static double probability(int k, int n)
    {
        double ans = 0;
        for (int i = k; i <= n; ++ i)
      
            // Probability of getting exactly i
            // heads out of n heads
            ans += fact[n] / (fact[i] * fact[n-i]);
      
        // Note: 1 << n = pow(2, n)
        ans = ans / (1 << n);
        return ans;
    }
      
    public static void precompute()
    {
        // Preprocess all factorial only upto 19,
        // as after that it will overflow
        fact[0] = fact[1] = 1;
      
        for (int i = 2; i < 20; ++i)
            fact[i] = fact[i - 1] * i;
    }
      
    // Driver code
    public static void main(String[] args)
    {
        fact = new double[100];
        precompute();
      
        // Probability of getting 2 head out
        // of 3 coins
        System.out.println(probability(2, 3));
      
        // Probability of getting 3 head out
        // of 6 coins
        System.out.println(probability(3, 6));
      
        // Probability of getting 12 head out
        // of 18 coins
        System.out.println(probability(12, 18));
      
    }
 }
// This code is contributed by Arnav Kr. Mandal

Python3

# Naive approach in Python3
# to find probability of
# at least k heads
 
MAX=21
 
fact=[0]*MAX
 
# Returns probability of
# getting at least k
# heads in n tosses.
def probability(k, n):
    ans = 0
    for i in range(k,n+1):
 
        # Probability of getting exactly i
        # heads out of n heads
        ans += fact[n] / (fact[i] * fact[n - i])
 
    # Note: 1 << n = pow(2, n)
    ans = ans / (1 << n)
    return ans
 
def precompute():
     
    # Preprocess all factorial
    # only upto 19,
    # as after that it
    # will overflow
    fact[0] = 1
    fact[1] = 1
 
    for i in range(2,20):
        fact[i] = fact[i - 1] * i
 
# Driver code
if __name__=='__main__':
    precompute()
 
    # Probability of getting 2
    # head out of 3 coins
    print(probability(2, 3))
 
    # Probability of getting
    # 3 head out of 6 coins
    print(probability(3, 6))
 
    # Probability of getting
    # 12 head out of 18 coins
    print(probability(12, 18))
     
# This code is contributed by
# mits

C#

// C# Code for Probability of getting
// atleast K heads in N tosses of Coins
using System;
 
class GFG
{
     
    public static double []fact;
     
    // Returns probability of getting at least k
    // heads in n tosses.
    public static double probability(int k, int n)
    {
        double ans = 0;
        for (int i = k; i <= n; ++ i)
     
            // Probability of getting exactly i
            // heads out of n heads
            ans += fact[n] / (fact[i] * fact[n - i]);
     
        // Note: 1 << n = pow(2, n)
        ans = ans / (1 << n);
        return ans;
    }
     
    public static void precompute()
    {
        // Preprocess all factorial only upto 19,
        // as after that it will overflow
        fact[0] = fact[1] = 1;
     
        for (int i = 2; i < 20; ++i)
            fact[i] = fact[i - 1] * i;
    }
     
    // Driver code
    public static void Main()
    {
        fact = new double[100];
        precompute();
     
        // Probability of getting 2 head out
        // of 3 coins
        Console.WriteLine(probability(2, 3));
     
        // Probability of getting 3 head out
        // of 6 coins
        Console.WriteLine(probability(3, 6));
     
        // Probability of getting 12 head out
        // of 18 coins
        Console.Write(probability(12, 18));
     
    }
}
// This code is contributed by nitin mittal.

PHP

<?php
// Naive approach in PHP to find
// probability of at least k heads
$MAX = 21;
 
$fact = array_fill(0, $MAX, 0);
 
// Returns probability of getting
// at least k heads in n tosses.
function probability($k, $n)
{
    global $fact;
    $ans = 0;
    for ($i = $k; $i <= $n; ++$i)
 
        // Probability of getting exactly
        // i heads out of n heads
        $ans += $fact[$n] / ($fact[$i] *
                             $fact[$n - $i]);
 
    // Note: 1 << n = pow(2, n)
    $ans = $ans / (1 << $n);
    return $ans;
}
 
function precompute()
{
    global $fact;
     
    // Preprocess all factorial only
    // upto 19, as after that it
    // will overflow
    $fact[0] = $fact[1] = 1;
 
    for ($i = 2; $i < 20; ++$i)
        $fact[$i] = $fact[$i - 1] * $i;
}
 
// Driver code
precompute();
 
// Probability of getting 2
// head out of 3 coins
echo number_format(probability(2, 3), 6) . "\n";
 
// Probability of getting 3
// head out of 6 coins
echo number_format(probability(3, 6), 6) . "\n";
 
// Probability of getting 12
// head out of 18 coins
echo number_format(probability(12, 18), 6);
     
// This code is contributed by mits
?>

Javascript

<script>
 
// javascript Code for Probability of getting
// atleast K heads in N tosses of Coins
 
 
let fact;
 
    // Returns probability of getting at least k
    // heads in n tosses.
    function probability( k, n) {
        let ans = 0, i;
        for ( i = k; i <= n; ++i)
 
            // Probability of getting exactly i
            // heads out of n heads
            ans += fact[n] / (fact[i] * fact[n - i]);
 
        // Note: 1 << n = pow(2, n)
        ans = ans / (1 << n);
        return ans;
    }
 
     function precompute() {
        // Preprocess all factorial only upto 19,
        // as after that it will overflow
        fact[0] = fact[1] = 1;
 
        for ( let i = 2; i < 20; ++i)
            fact[i] = fact[i - 1] * i;
    }
 
    // Driver code
      
        fact = Array(100).fill(0);
        precompute();
 
        // Probability of getting 2 head out
        // of 3 coins
        document.write(probability(2, 3)+"<br/>");
 
        // Probability of getting 3 head out
        // of 6 coins
        document.write(probability(3, 6)+"<br/>");
 
        // Probability of getting 12 head out
        // of 18 coins
        document.write(probability(12, 18).toFixed(6)+"<br/>");
 
 
 
// This code is contributed by shikhasingrajput
 
</script>

Producción: 

0.5
0.65625
0.118942

Complejidad de Tiempo: O(n) donde n < 20 
Espacio auxiliar: O(n)
Método 2 (Programación Dinámica y Registro) 
Otra forma es usar programación Dinámica y logaritmo. log() es realmente útil para almacenar el factorial de cualquier número sin preocuparse por el desbordamiento. Veamos cómo lo usamos:
 

At first let see how n! can be written.
n! = n * (n-1) * (n-2) * (n-3) * ... * 3 * 2 * 1

Now take log on base 2 both the sides as:
=> log(n!) = log(n) + log(n-1) + log(n-2) + ... + log(3) 
         + log(2) + log(1)

Now whenever we need to find the factorial of any number, we can use
this precomputed value. For example:
Suppose if we want to find the value of nCi which can be written as:
=> nCi = n! / (i! * (n-i)! )

Taking log2() both sides as:
=> log2 (nCi) = log2 ( n! / (i! * (n-i)! ) )
=> log2 (nCi) = log2 ( n! ) - log2(i!) - log2( (n-i)! )  `

Putting dp[num] = log2 (num!), we get:
=> log2 (nCi) = dp[n] - dp[i] - dp[n-i] 

But as we see in above relation there is an extra factor of 2n which
tells the probability of getting i heads, so
=> log2 (2n) = n.

We will subtract this n from above result to get the final answer:
=> Pi (log2 (nCi)) = dp[n] - dp[i] - dp[n-i] - n

Now: Pi (nCi) = 2 dp[n] - dp[i] - dp[n-i] - n

Tada! Now the questions boils down the summation of Pi for all i in
[k, n] will yield the answer which can be calculated easily without
overflow.

A continuación se muestran los códigos para ilustrar esto:
 

C++

// Dynamic and Logarithm approach find probability of
// at least k heads
#include<bits/stdc++.h>
using namespace std;
#define MAX 100001
 
// dp[i] is going to store Log ( i !) in base 2
double dp[MAX];
 
double probability(int k, int n)
{
    double ans = 0; // Initialize result
 
    // Iterate from k heads to n heads
    for (int i=k; i <= n; ++i)
    {
        double res = dp[n] - dp[i] - dp[n-i] - n;
        ans += pow(2.0, res);
    }
 
    return ans;
}
 
void precompute()
{
    // Preprocess all the logarithm value on base 2
    for (int i=2; i < MAX; ++i)
        dp[i] = log2(i) + dp[i-1];
}
 
// Driver code
int main()
{
    precompute();
 
    // Probability of getting 2 head out of 3 coins
    cout << probability(2, 3) << "\n";
 
    // Probability of getting 3 head out of 6 coins
    cout << probability(3, 6) << "\n";
 
    // Probability of getting 500 head out of 10000 coins
    cout << probability(500, 1000);
 
    return 0;
}

Java

// Dynamic and Logarithm approach find probability of
// at least k heads
import java.math.*;
class GFG {
     
static int MAX = 100001;
 
// dp[i] is going to store Log ( i !) in base 2
static double dp[] = new double[MAX];
 
static double probability(int k, int n)
{
    double ans = 0.0; // Initialize result
 
    // Iterate from k heads to n heads
    for (int i=k; i <= n; ++i)
    {
        double res = dp[n] - dp[i] - dp[n-i] - n;
        ans += Math.pow(2.0, res);
    }
 
    return ans;
}
 
static void precompute()
{
    // Preprocess all the logarithm value on base 2
    for (int i=2; i < MAX; ++i)
        dp[i] = (Math.log(i)/Math.log(2)) + dp[i-1];
}
 
// Driver code
public static void main(String args[])
{
    precompute();
 
    // Probability of getting 2 head out of 3 coins
    System.out.println(probability(2, 3));
 
    // Probability of getting 3 head out of 6 coins
    System.out.println(probability(3, 6));
 
    // Probability of getting 500 head out of 10000 coins
    System.out.println(probability(500, 1000));
}
 
}

Python3

# Dynamic and Logarithm approach find probability of
# at least k heads
 
from math import log2
MAX=100001
 
# dp[i] is going to store Log ( i !) in base 2
dp=[0]*MAX
 
def probability( k, n):
 
    ans = 0 # Initialize result
 
    # Iterate from k heads to n heads
    for i in range(k,n+1):
 
        res = dp[n] - dp[i] - dp[n-i] - n
        ans = ans + pow(2.0, res)
     
 
    return ans
 
 
def precompute():
 
    # Preprocess all the logarithm value on base 2
    for i in range(2,MAX):
        dp[i] = log2(i) + dp[i-1]
 
 
# Driver code
if __name__=='__main__':
    precompute()
 
    # Probability of getting 2 head out of 3 coins
    print(probability(2, 3))
 
    # Probability of getting 3 head out of 6 coins
    print(probability(3, 6))
 
    # Probability of getting 500 head out of 10000 coins
    print(probability(500, 1000))
 
#this code is contributed by ash264

C#

// Dynamic and Logarithm approach find probability of
// at least k heads
using System;
 
class GFG
{
     
static int MAX = 100001;
 
// dp[i] is going to store Log ( i !) in base 2
static double[] dp = new double[MAX];
 
static double probability(int k, int n)
{
    double ans = 0.0; // Initialize result
 
    // Iterate from k heads to n heads
    for (int i = k; i <= n; ++i)
    {
        double res = dp[n] - dp[i] - dp[n-i] - n;
        ans += Math.Pow(2.0, res);
    }
    return ans;
}
 
static void precompute()
{
    // Preprocess all the logarithm value on base 2
    for (int i = 2; i < MAX; ++i)
        dp[i] = (Math.Log(i) / Math.Log(2)) + dp[i - 1];
}
 
// Driver code
public static void Main()
{
    precompute();
 
    // Probability of getting 2 head out of 3 coins
    Console.WriteLine(probability(2, 3));
 
    // Probability of getting 3 head out of 6 coins
    Console.WriteLine(probability(3, 6));
 
    // Probability of getting 500 head out of 10000 coins
    Console.WriteLine(Math.Round(probability(500, 1000),6));
}
}
 
// This code is contributed by mits

PHP

<?php
// Dynamic and Logarithm approach
// find probability of at least k heads
$MAX = 100001;
 
// dp[i] is going to store
// Log ( i !) in base 2
$dp = array_fill(0, $MAX, 0);
 
function probability($k, $n)
{
    global $MAX, $dp;
    $ans = 0; // Initialize result
 
    // Iterate from k heads to n heads
    for ($i = $k; $i <= $n; ++$i)
    {
        $res = $dp[$n] - $dp[$i] -
               $dp[$n - $i] - $n;
        $ans += pow(2.0, $res);
    }
 
    return $ans;
}
 
function precompute()
{
    global $MAX, $dp;
     
    // Preprocess all the logarithm
    // value on base 2
    for ($i = 2; $i < $MAX; ++$i)
     
        // Note : log2() function is not in php
        // Some OUTPUT very in their decimal point
        // Basically log(value,base) is work as
        // this logic : "log10(value)/log10(2)"
        // equals to log2(value)
        $dp[$i] = log($i, 2) + $dp[$i - 1];
}
 
// Driver code
precompute();
 
// Probability of getting 2
// head out of 3 coins
echo probability(2, 3)."\n";
 
// Probability of getting 3
// head out of 6 coins
echo probability(3, 6)."\n";
 
// Probability of getting 500
// head out of 10000 coins
echo probability(500, 1000);
 
// This code is contributed by mits
?>

Javascript

<script>
// Dynamic and Logarithm approach find probability of
// at least k heads
    let MAX = 100001;
 
    // dp[i] is going to store Log ( i !) in base 2
    let dp = new Array(MAX).fill(0);
 
    function probability(k , n)
    {
        var ans = 0.0; // Initialize result
 
        // Iterate from k heads to n heads
        for (let i = k; i <= n; ++i)
        {
            var res = dp[n] - dp[i] - dp[n - i] - n;
            ans += Math.pow(2.0, res);
        }
 
        return ans;
    }
 
    function precompute()
    {
     
        // Preprocess all the logarithm value on base 2
        for (let i = 2; i < MAX; ++i)
            dp[i] = (Math.log(i) / Math.log(2)) + dp[i - 1];
    }
 
    // Driver code
    precompute();
 
    // Probability of getting 2 head out of 3 coins
    document.write(probability(2, 3).toFixed(2)+"<br/>");
 
    // Probability of getting 3 head out of 6 coins
    document.write(probability(3, 6).toFixed(5)+"<br/>");
 
    // Probability of getting 500 head out of 10000 coins
    document.write(probability(500, 1000).toFixed(6)+"<br/>");   
 
// This code is contributed by Amit Katiyar
</script>

Producción: 
 

0.5
0.65625
0.512613

Complejidad de tiempo: O(n) 
Espacio auxiliar: O(n) 
Este enfoque es beneficioso para valores grandes de n que van de 1 a 10 6 Shubham Bansal
contribuye con este artículo . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

 

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *