La paradoja de Simpson en términos sencillos es la inversión de la relación dentro de los datos con respecto a los subgrupos de datos después de combinar esos datos de subgrupos.
Por ejemplo, si hay dos departamentos en una universidad y ambos tienen una alta probabilidad de que una mujer sea aceptada, luego de combinar sus datos por intuición, la probabilidad general de aceptación de la mujer debería ser alta, pero esto puede no ser cierto.
Dado matemáticamente
, a1/b1 < c1/d1 y a2/b2 < c2/d2 entonces (a1+a2)/(b1+b2) < (c1+c2)/(d1+d2)?
Simpson’s Paradox dice que puede no ser cierto.
7/8 < 2/2 and 1/2 < 5/8 yet, (7+1)/(2+2) > (2+5)/(2+8)
Un caso similar se vio en la demanda contra UC Berkeley con respecto a los datos de admisión que mostraban que los hombres tenían una mayor probabilidad de que se aceptaran las requests que la solicitud de la mujer. Pero después de examinar los departamentos individuales, se consideró un escenario inverso, ya que la mayoría de los departamentos favorecían a las mujeres sobre los hombres.
| Solicitantes | Aceptado | |
|---|---|---|
| Hombres | 8442 | 44% |
| Mujeres | 4321 | 35% |
| Departamentos | Hombres | Mujeres | ||
|---|---|---|---|---|
| Solicitantes | Aceptado | Solicitantes | Aceptado | |
| A | 825 | 62% | 108 | |
| B | 560 | 63% | 25 | |
| C | 325 | 593 | 34% | |
| D | 417 | 33% | 375 | |
| mi | 191 | 393 | 24% | |
| F | 272 | 6% | 341 | |
¿Por qué estaba pasando esto ?
Motivo:
este tipo de comportamiento se observó porque más mujeres postulaban a departamentos competitivos con bajas tasas de admisión, mientras que más hombres postulaban a departamentos menos competitivos con
altas tasas de aceptación.
Podemos ver en la tabla que 825 hombres se han postulado en comparación con 108 mujeres en el departamento A de alta tasa de aceptación . Mientras que más niñas están solicitando en departamentos con tasas bajas como F y E. Lo que finalmente llevó a que más hombres fueran aceptados por la universidad que mujeres.
Otro ejemplo:
supongamos que tenemos una configuración como la que se muestra en la figura siguiente con dos tipos de frijoles de color verde y azul.
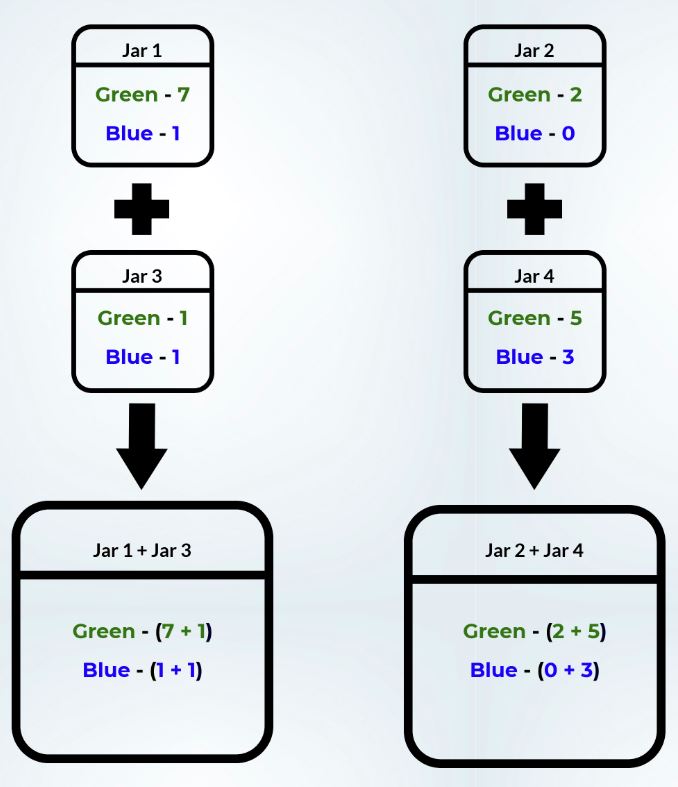
Antes de mezclar:
probabilidad de sacar una judía verde del tarro,
7/8 < 2/2 (Jar1) (Jar2) 1/2 < 5/8 (Jar3) (Jar4)
Después de mezclar:
probabilidad de sacar una judía verde del tarro
8/10 > 7/10 Inequality (Jar1 + Jar3) (Jar2 + Jar4)
Aquí también podemos ver que inicialmente los frascos 1 y 3 tenían una mayor probabilidad de recolectar judías verdes que el frasco 2 y el frasco 4 respectivamente, pero después de mezclar el contenido de los frascos, la relación se invirtió. Después de mezclar, el contenido combinado del Tarro 2 y el Tarro 4 tenía una mayor probabilidad de cosechar judías verdes. Este es un ejemplo muy simple de la paradoja de Simpson.