Problema de asignación de trabajo usando Branch And Bound – Part 1

Que haya N trabajadores y N puestos de trabajo. Cualquier trabajador puede ser asignado para realizar cualquier trabajo, incurriendo en un costo que puede variar dependiendo de la asignación de trabajo. Se requiere realizar todos los trabajos asignando exactamente un trabajador a cada trabajo y exactamente un trabajo a cada agente de tal manera que se minimice el costo total de la asignación.

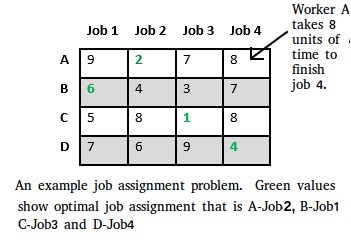
Exploremos todos los enfoques para este problema.

Solución 1: Fuerza bruta 
¡Generamos n! posibles asignaciones de trabajo y para cada una de esas asignaciones, calculamos su costo total y devolvemos la asignación menos costosa. Como la solución es una permutación de los n trabajos, su complejidad es O(n!).

Solución 2: algoritmo húngaro 
La asignación óptima se puede encontrar utilizando el algoritmo húngaro. El algoritmo húngaro tiene una complejidad de tiempo de ejecución en el peor de los casos de O (n ^ 3).

Solución 3: DFS/BFS en árbol de espacio de 
estado Un árbol de espacio de estado es un árbol N-ario con la propiedad de que cualquier ruta desde la raíz hasta el Node hoja contiene una de las muchas soluciones para un problema dado. Podemos realizar una búsqueda en profundidad en el árbol de espacio de estado y, sin embargo, los movimientos sucesivos pueden alejarnos de la meta en lugar de acercarnos. La búsqueda del árbol de espacio de estado sigue el camino más a la izquierda desde la raíz, independientemente del estado inicial. Es posible que nunca se encuentre un Node de respuesta en este enfoque. También podemos realizar una búsqueda en anchura en el árbol de espacio de estado. Pero no importa cuál sea el estado inicial, el algoritmo intenta la misma secuencia de movimientos como DFS.

Solución 4: Encontrar la solución óptima usando Branch and Bound 
La regla de selección para el siguiente Node en BFS y DFS es «ciega». es decir, la regla de selección no da ninguna preferencia a un Node que tiene una muy buena posibilidad de llevar rápidamente la búsqueda a un Node de respuesta. La búsqueda de una solución óptima a menudo se puede acelerar mediante el uso de una función de clasificación «inteligente», también llamada función de costo aproximado para evitar buscar en subárboles que no contienen una solución óptima. Es similar a la búsqueda tipo BFS pero con una optimización importante. En lugar de seguir el orden FIFO, elegimos un Node vivo con el menor costo. Es posible que no obtengamos una solución óptima siguiendo el Node con el costo menos prometedor, pero brindará una muy buena oportunidad de llevar la búsqueda a un Node de respuesta rápidamente.

Hay dos enfoques para calcular la función de costo:  

1. Para cada trabajador, elegimos el trabajo con el costo mínimo de la lista de trabajos no asignados (toma la entrada mínima de cada fila).
2. Para cada trabajo, elegimos un trabajador con el costo más bajo para ese trabajo de la lista de trabajadores no asignados (tome la entrada mínima de cada columna).

En este artículo se sigue el primer enfoque.

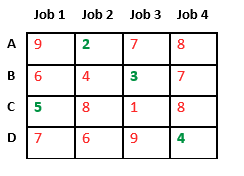
Tomemos el siguiente ejemplo e intentemos calcular el costo prometedor cuando el trabajo 2 se asigna al trabajador A. 

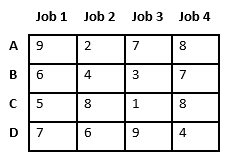
Dado que el Trabajo 2 se asigna al trabajador A (marcado en verde), el costo se convierte en 2 y el Trabajo 2 y el trabajador A no están disponibles (marcados en rojo). 

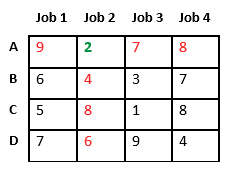
Ahora asignamos el trabajo 3 al trabajador B ya que tiene un costo mínimo de la lista de trabajos no asignados. El costo se convierte en 2 + 3 = 5 y el Trabajo 3 y el trabajador B también dejan de estar disponibles. 

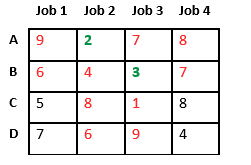
Finalmente, el trabajo 1 se asigna al trabajador C ya que tiene un costo mínimo entre los trabajos no asignados y el trabajo 4 se asigna al trabajador C ya que solo queda Trabajo. El costo total se convierte en 2 + 3 + 5 + 4 = 14. 

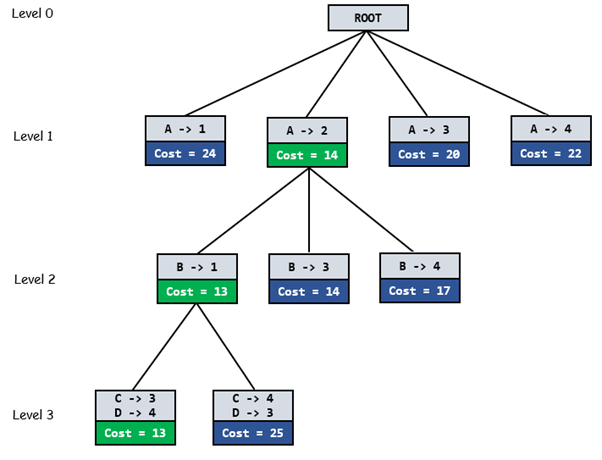
El siguiente diagrama muestra un diagrama de espacio de búsqueda completo que muestra la ruta de solución óptima en verde. 

Algoritmo completo: 

/* findMinCost uses Least() and Add() to maintain the
   list of live nodes

   Least() finds a live node with least cost, deletes
   it from the list and returns it

   Add(x) calculates cost of x and adds it to the list
   of live nodes

   Implements list of live nodes as a min heap */


// Search Space Tree Node
node
{
   int job_number;
   int worker_number;
   node parent;
   int cost;
}

// Input: Cost Matrix of Job Assignment problem
// Output: Optimal cost and Assignment of Jobs
algorithm findMinCost (costMatrix mat[][])
{
   // Initialize list of live nodes(min-Heap)
   // with root of search tree i.e. a Dummy node
   while (true)
   {
      // Find a live node with least estimated cost
      E = Least();

      // The found node is deleted from the list
      // of live nodes
      if (E is a leaf node)
      {
         printSolution();
         return;
      }

     for each child x of E
     {
         Add(x); // Add x to list of live nodes;
         x->parent = E; // Pointer for path to root
     }
   }
} 

A continuación se muestra su implementación en C++. 

// Program to solve Job Assignment problem
// using Branch and Bound
#include <bits/stdc++.h>
using namespace std;
#define N 4
  
// state space tree node
struct Node
{
    // stores parent node of current node
    // helps in tracing path when answer is found
    Node* parent;
  
    // contains cost for ancestors nodes
    // including current node
    int pathCost;
  
    // contains least promising cost
    int cost;
  
    // contain worker number
    int workerID;
  
    // contains Job ID
    int jobID;
  
    // Boolean array assigned will contains
    // info about available jobs
    bool assigned[N];
};
  
// Function to allocate a new search tree node
// Here Person x is assigned to job y
Node* newNode(int x, int y, bool assigned[],
              Node* parent)
{
    Node* node = new Node;
  
    for (int j = 0; j < N; j++)
        node->assigned[j] = assigned[j];
    node->assigned[y] = true;
  
    node->parent = parent;
    node->workerID = x;
    node->jobID = y;
  
    return node;
}
  
// Function to calculate the least promising cost
// of node after worker x is assigned to job y.
int calculateCost(int costMatrix[N][N], int x,
                  int y, bool assigned[])
{
    int cost = 0;
  
    // to store unavailable jobs
    bool available[N] = {true};
  
    // start from next worker
    for (int i = x + 1; i < N; i++)
    {
        int min = INT_MAX, minIndex = -1;
  
        // do for each job
        for (int j = 0; j < N; j++)
        {
            // if job is unassigned
            if (!assigned[j] && available[j] &&
                costMatrix[i][j] < min)
            {
                // store job number
                minIndex = j;
  
                // store cost
                min = costMatrix[i][j];
            }
        }
  
        // add cost of next worker
        cost += min;
  
        // job becomes unavailable
        available[minIndex] = false;
    }
  
    return cost;
}
  
// Comparison object to be used to order the heap
struct comp
{
    bool operator()(const Node* lhs,
                   const Node* rhs) const
    {
        return lhs->cost > rhs->cost;
    }
};
  
// print Assignments
void printAssignments(Node *min)
{
    if(min->parent==NULL)
        return;
  
    printAssignments(min->parent);
    cout << "Assign Worker " << char(min->workerID + 'A')
         << " to Job " << min->jobID << endl;
  
}
  
// Finds minimum cost using Branch and Bound.
int findMinCost(int costMatrix[N][N])
{
    // Create a priority queue to store live nodes of
    // search tree;
    priority_queue<Node*, std::vector<Node*>, comp> pq;
  
    // initialize heap to dummy node with cost 0
    bool assigned[N] = {false};
    Node* root = newNode(-1, -1, assigned, NULL);
    root->pathCost = root->cost = 0;
    root->workerID = -1;
  
    // Add dummy node to list of live nodes;
    pq.push(root);
  
    // Finds a live node with least cost,
    // add its childrens to list of live nodes and
    // finally deletes it from the list.
    while (!pq.empty())
    {
      // Find a live node with least estimated cost
      Node* min = pq.top();
  
      // The found node is deleted from the list of
      // live nodes
      pq.pop();
  
      // i stores next worker
      int i = min->workerID + 1;
  
      // if all workers are assigned a job
      if (i == N)
      {
          printAssignments(min);
          return min->cost;
      }
  
      // do for each job
      for (int j = 0; j < N; j++)
      {
        // If unassigned
        if (!min->assigned[j])
        {
          // create a new tree node
          Node* child = newNode(i, j, min->assigned, min);
  
          // cost for ancestors nodes including current node
          child->pathCost = min->pathCost + costMatrix[i][j];
  
          // calculate its lower bound
          child->cost = child->pathCost +
            calculateCost(costMatrix, i, j, child->assigned);
  
          // Add child to list of live nodes;
          pq.push(child);
        }
      }
    }
}
  
// Driver code
int main()
{
    // x-coordinate represents a Worker
    // y-coordinate represents a Job
    int costMatrix[N][N] =
    {
        {9, 2, 7, 8},
        {6, 4, 3, 7},
        {5, 8, 1, 8},
        {7, 6, 9, 4}
    };
  
  
    /* int costMatrix[N][N] =
    {
        {82, 83, 69, 92},
        {77, 37, 49, 92},
        {11, 69,  5, 86},
        { 8,  9, 98, 23}
    };
    */
  
    /* int costMatrix[N][N] =
    {
        {2500, 4000, 3500},
        {4000, 6000, 3500},
        {2000, 4000, 2500}
    };*/
  
    /*int costMatrix[N][N] =
    {
        {90, 75, 75, 80},
        {30, 85, 55, 65},
        {125, 95, 90, 105},
        {45, 110, 95, 115}
    };*/
  
  
    cout << "\nOptimal Cost is "
        << findMinCost(costMatrix);
  
    return 0;
}

Producción : 

Assign Worker A to Job 1
Assign Worker B to Job 0
Assign Worker C to Job 2
Assign Worker D to Job 3

Optimal Cost is 13

Referencia: 
www.cs.umsl.edu/~sanjiv/classes/cs5130/lectures/bb.pdf

Este artículo es una contribución de Aditya Goel . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.