Problema de detención en la teoría de la computación

Para comprender mejor el problema de la detención, debemos conocer la Decidibilidad , la Indecidibilidad y la máquina de Turing , los problemas de decisión y también una teoría denominada Teoría de la Computabilidad y Teoría de la Complejidad Computacional.

Algunos términos importantes:

• Teoría de la computabilidad:
  la rama de la teoría de la computación que estudia qué problemas se pueden resolver computacionalmente utilizando un modelo diferente. En informática, la complejidad computacional, o simplemente complejidad de un algoritmo, es la cantidad de recursos necesarios para ejecutarlo.
• Problemas de decisión:
  un problema de decisión tiene solo dos salidas posibles (sí o no) en cualquier entrada. En la teoría de la computabilidad y la teoría de la complejidad computacional, un problema de decisión es un problema que se puede plantear como una pregunta de sí o no de los valores de entrada. ¿Hay alguna solución a un problema en particular? La respuesta sería un sí o un no. Un problema de decisión es cualquier pregunta arbitraria de sí/no en un conjunto infinito de entradas.
• Máquina de Turing:
  una máquina de Turing es un modelo matemático de computación. Una máquina de Turing es un ejemplo general de una CPU que controla toda la manipulación de datos realizada por una computadora. La máquina de Turing puede detenerse o no detenerse y depende del algoritmo y la entrada asociada con el algoritmo.

Ahora, analicemos el problema de la detención:

El problema de la detención: dado un programa/algoritmo, ¿alguna vez se detendrá o no?
Detener significa que el programa en cierta entrada lo aceptará y se detendrá o lo rechazará y se detendrá y nunca entrará en un bucle infinito. Básicamente, detener significa terminar. Entonces, ¿podemos tener un algoritmo que diga si el programa dado se detendrá o no? En términos de la máquina de Turing, ¿terminará cuando se ejecute en alguna máquina con alguna string de entrada dada en particular?

La respuesta es no, no podemos diseñar un algoritmo generalizado que pueda decir apropiadamente que un programa determinado alguna vez se detendrá o no.
La única forma es ejecutar el programa y verificar si se detiene o no.
También podemos abstenernos de la pregunta del problema de detención de esta manera: Dado un programa escrito en algún lenguaje de programación (c/c++/java), ¿alguna vez entrará en un ciclo infinito (el ciclo nunca se detiene) o siempre terminará (detener)?

Este es un problema indecidible porque no podemos tener un algoritmo que nos diga si un programa determinado se detendrá o no de forma generalizada, es decir, teniendo un programa/algoritmo específico. En general, no siempre podemos saber por eso no podemos tener un algoritmo general. La mejor manera posible es ejecutar el programa y ver si se detiene o no. De esta manera, para muchos programas podemos ver que a veces se repite y siempre se detiene.

Prueba por contradicción –
Declaración del problema: ¿Podemos diseñar una máquina que, si se le da un programa, pueda averiguar si ese programa siempre se detendrá o no en una entrada en particular?

Solución: Supongamos que podemos diseñar ese tipo de máquina llamada HM(P, I) donde HM es la máquina/programa, P es el programa e I es la entrada. Al recibir ambos argumentos, la máquina HM dirá que el programa P se detiene o no.
Si podemos diseñar un programa de este tipo, esto nos permite escribir otro programa que llamamos a este programa CM(X) donde X es cualquier programa (tomado como argumento) y de acuerdo con la definición del programa CM(X) que se muestra en la figura.

En el programa CM(X) llamamos a la función HM(X), que ya hemos definido y a HM() le pasamos los argumentos (X, X), según la definición de HM() puede tomar dos argumentos, es decir uno es el programa y otro es la entrada. Ahora, en el segundo programa, pasamos X como programa y X como entrada a la función HM(). Sabemos que el programa HM() da dos salidas, ya sea «Detener» o «No detener ”.Pero en el caso del segundo programa, cuando HM(X, X) detendrá el bucle, el cuerpo le indicará que entre en el bucle y cuando no se detenga, eso significará un bucle, se le pedirá que regrese.

Ahora tomamos una situación más en la que el programa CM se pasa a la función CM() como argumento. Entonces habría alguna imposibilidad, es decir, surge una condición que no es posible.

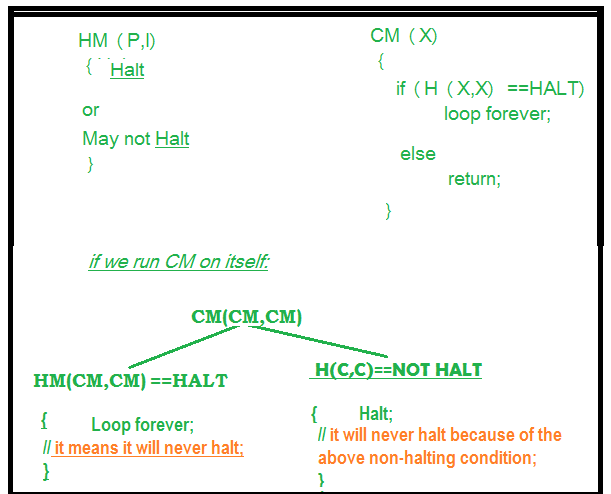
Es imposible que la función externa se detenga si su código (cuerpo interno) está en bucle y también es imposible que la función externa que no se detenga se detenga incluso después de que su código interno se detenga. Entonces, ambas condiciones no se detienen para la máquina/programa CM, incluso si habíamos asumido al principio que se detendría. Entonces, esta es la contradicción y podemos decir que nuestra suposición era incorrecta y este problema, es decir, el problema de la detención es indecidible.

Así demostramos que el problema de la detención es indecidible.