Un Clique es un subgrafo de un grafo tal que todos los vértices del subgrafo están completamente conectados entre sí. Dado un gráfico, encuentre si se puede dividir en dos camarillas.
Ejemplos:
Input : G[][] = {{0, 1, 1, 0, 0},
{1, 0, 1, 1, 0},
{1, 1, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 0, 0, 1, 0}};
Output : Yes
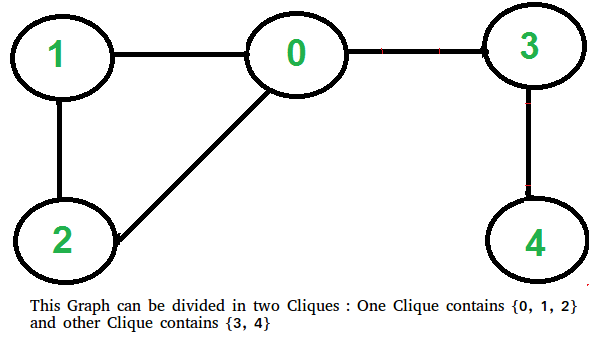
Este problema parece complicado al principio, pero tiene una solución simple e interesante. Un grafo se puede dividir en dos cliques si su grafo complementario es bipartito . Entonces, a continuación hay dos pasos para encontrar si el gráfico se puede dividir en dos camarillas o no.
- Encuentre el complemento de Graph. A continuación se muestra el gráfico de complemento que se muestra arriba. En complemento, se eliminan todos los bordes originales. Y los vértices que no tenían una arista entre ellos, ahora tienen una arista que los conecta.
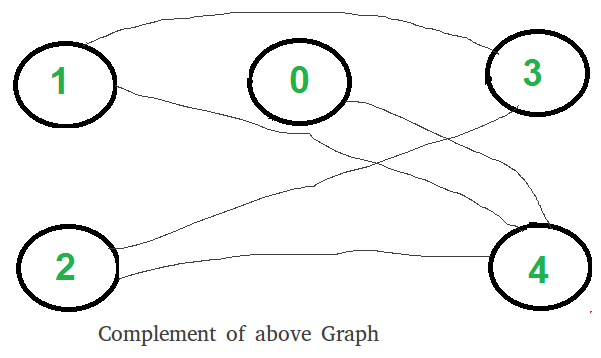
- Devuelve verdadero si el complemento es bipartito, de lo contrario, falso. El gráfico que se muestra arriba es bipartito. Aquí se analiza si un gráfico es bipartito o no .
¿Como funciona esto?
Si el complemento es bipartito, entonces el gráfico se puede dividir en dos conjuntos U y V de modo que no haya un borde que se conecte a los vértices del mismo conjunto. Esto significa que en el gráfico original, estos conjuntos U y V están completamente conectados. Por lo tanto, el gráfico original podría dividirse en dos camarillas.
Implementación:
A continuación se muestra la implementación de los pasos anteriores.
C++
// C++ program to find out whether a given graph can be
// converted to two Cliques or not.
#include <bits/stdc++.h>
using namespace std;
const int V = 5;
// This function returns true if subgraph reachable from
// src is Bipartite or not.
bool isBipartiteUtil(int G[][V], int src, int colorArr[])
{
colorArr[src] = 1;
// Create a queue (FIFO) of vertex numbers and enqueue
// source vertex for BFS traversal
queue <int> q;
q.push(src);
// Run while there are vertices in queue (Similar to BFS)
while (!q.empty())
{
// Dequeue a vertex from queue
int u = q.front();
q.pop();
// Find all non-colored adjacent vertices
for (int v = 0; v < V; ++v)
{
// An edge from u to v exists and destination
// v is not colored
if (G[u][v] && colorArr[v] == -1)
{
// Assign alternate color to this adjacent
// v of u
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
// An edge from u to v exists and destination
// v is colored with same color as u
else if (G[u][v] && colorArr[v] == colorArr[u])
return false;
}
}
// If we reach here, then all adjacent vertices can
// be colored with alternate color
return true;
}
// Returns true if a Graph G[][] is Bipartite or not. Note
// that G may not be connected.
bool isBipartite(int G[][V])
{
// Create a color array to store colors assigned
// to all vertices. Vertex number is used as index in
// this array. The value '-1' of colorArr[i]
// is used to indicate that no color is assigned to
// vertex 'i'. The value 1 is used to indicate first
// color is assigned and value 0 indicates
// second color is assigned.
int colorArr[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
// One by one check all not yet colored vertices.
for (int i = 0; i < V; i++)
if (colorArr[i] == -1)
if (isBipartiteUtil(G, i, colorArr) == false)
return false;
return true;
}
// Returns true if G can be divided into
// two Cliques, else false.
bool canBeDividedinTwoCliques(int G[][V])
{
// Find complement of G[][]
// All values are complemented except
// diagonal ones
int GC[V][V];
for (int i=0; i<V; i++)
for (int j=0; j<V; j++)
GC[i][j] = (i != j)? !G[i][j] : 0;
// Return true if complement is Bipartite
// else false.
return isBipartite(GC);
}
// Driver program to test above function
int main()
{
int G[][V] = {{0, 1, 1, 1, 0},
{1, 0, 1, 0, 0},
{1, 1, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 0, 0, 1, 0}
};
canBeDividedinTwoCliques(G) ? cout << "Yes" :
cout << "No";
return 0;
}
Java
// Java program to find out whether a given graph can be
// converted to two Cliques or not.
import java.util.ArrayDeque;
import java.util.Deque;
class GFG {
static int V = 5;
// This function returns true if subgraph reachable from
// src is Bipartite or not.
static boolean isBipartiteUtil(int G[][], int src, int colorArr[])
{
colorArr[src] = 1;
// Create a queue (FIFO) of vertex numbers and enqueue
// source vertex for BFS traversal
Deque <Integer> q = new ArrayDeque<>();
q.push(src);
// Run while there are vertices in queue (Similar to BFS)
while (!q.isEmpty())
{
// Dequeue a vertex from queue
int u = q.peek();
q.pop();
// Find all non-colored adjacent vertices
for (int v = 0; v < V; ++v)
{
// An edge from u to v exists and destination
// v is not colored
if (G[u][v] == -1 && colorArr[v] == -1)
{
// Assign alternate color to this adjacent
// v of u
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
// An edge from u to v exists and destination
// v is colored with same color as u
else if (G[u][v] == colorArr[u] && colorArr[v] == colorArr[u])
return false;
}
}
// If we reach here, then all adjacent vertices can
// be colored with alternate color
return true;
}
// Returns true if a Graph G[][] is Bipartite or not. Note
// that G may not be connected.
static boolean isBipartite(int G[][])
{
// Create a color array to store colors assigned
// to all vertices. Vertex number is used as index in
// this array. The value '-1' of colorArr[i]
// is used to indicate that no color is assigned to
// vertex 'i'. The value 1 is used to indicate first
// color is assigned and value 0 indicates
// second color is assigned.
int colorArr[]=new int[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
// One by one check all not yet colored vertices.
for (int i = 0; i < V; i++)
if (colorArr[i] == -1)
if (isBipartiteUtil(G, i, colorArr) == false)
return false;
return true;
}
// Returns true if G can be divided into
// two Cliques, else false.
static boolean canBeDividedinTwoCliques(int G[][])
{
// Find complement of G[][]
// All values are complemented except
// diagonal ones
int GC[][]=new int[V][V];
for (int i=0; i<V; i++)
for (int j=0; j<V; j++)
GC[i][j] = (i != j)? -GC[i][j] : 0;
// Return true if complement is Bipartite
// else false.
return isBipartite(GC);
}
// Driver program to test above function
public static void main(String[] args) {
int G[][] = {{0, 1, 1, 1, 0},
{1, 0, 1, 0, 0},
{1, 1, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 0, 0, 1, 0}
};
if(canBeDividedinTwoCliques(G))
System.out.println("Yes");
else
System.out.println("No");
}
}
/* This code contributed by PrinciRaj1992 */
Python3
# Python3 program to find out whether a given
# graph can be converted to two Cliques or not.
from queue import Queue
# This function returns true if subgraph
# reachable from src is Bipartite or not.
def isBipartiteUtil(G, src, colorArr):
global V
colorArr[src] = 1
# Create a queue (FIFO) of vertex numbers
# and enqueue source vertex for BFS traversal
q = Queue()
q.put(src)
# Run while there are vertices in
# queue (Similar to BFS)
while (not q.empty()):
# Dequeue a vertex from queue
u = q.get()
# Find all non-colored adjacent vertices
for v in range(V):
# An edge from u to v exists and
# destination v is not colored
if (G[u][v] and colorArr[v] == -1):
# Assign alternate color to this
# adjacent v of u
colorArr[v] = 1 - colorArr[u]
q.put(v)
# An edge from u to v exists and destination
# v is colored with same color as u
elif (G[u][v] and colorArr[v] == colorArr[u]):
return False
# If we reach here, then all adjacent
# vertices can be colored with alternate color
return True
# Returns true if a Graph G[][] is Bipartite or not.
# Note that G may not be connected.
def isBipartite(G):
global V
# Create a color array to store colors assigned
# to all vertices. Vertex number is used as index
# in this array. The value '-1' of colorArr[i]
# is used to indicate that no color is assigned
# to vertex 'i'. The value 1 is used to indicate
# first color is assigned and value 0 indicates
# second color is assigned.
colorArr = [-1] * V
# One by one check all not yet
# colored vertices.
for i in range(V):
if (colorArr[i] == -1):
if (isBipartiteUtil(G, i, colorArr) == False):
return False
return True
# Returns true if G can be divided into
# two Cliques, else false.
def canBeDividedinTwoCliques(G):
global V
# Find complement of G[][]
# All values are complemented
# except diagonal ones
GC = [[None] * V for i in range(V)]
for i in range(V):
for j in range(V):
GC[i][j] = not G[i][j] if i != j else 0
# Return true if complement is
# Bipartite else false.
return isBipartite(GC)
# Driver Code
V = 5
G = [[0, 1, 1, 1, 0],
[1, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 1, 0, 0, 1],
[0, 0, 0, 1, 0]]
if canBeDividedinTwoCliques(G):
print("Yes")
else:
print("No")
# This code is contributed by PranchalK
Javascript
<script>
// JavaScript program to find out whether a given graph can be
// converted to two Cliques or not.
const V = 5;
// This function returns true if subgraph reachable from
// src is Bipartite or not.
function isBipartiteUtil(G,src,colorArr)
{
colorArr[src] = 1;
// Create a queue (FIFO) of vertex numbers and enqueue
// source vertex for BFS traversal
let q = [];
q.push(src);
// Run while there are vertices in queue (Similar to BFS)
while (q.length > 0)
{
// Dequeue a vertex from queue
let u = q.shift();
// Find all non-colored adjacent vertices
for (let v = 0; v < V; ++v)
{
// An edge from u to v exists and destination
// v is not colored
if (G[u][v] && colorArr[v] == -1)
{
// Assign alternate color to this adjacent
// v of u
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
// An edge from u to v exists and destination
// v is colored with same color as u
else if (G[u][v] && colorArr[v] == colorArr[u])
return false;
}
}
// If we reach here, then all adjacent vertices can
// be colored with alternate color
return true;
}
// Returns true if a Graph G[][] is Bipartite or not. Note
// that G may not be connected.
function isBipartite(G)
{
// Create a color array to store colors assigned
// to all vertices. Vertex number is used as index in
// this array. The value '-1' of colorArr[i]
// is used to indicate that no color is assigned to
// vertex 'i'. The value 1 is used to indicate first
// color is assigned and value 0 indicates
// second color is assigned.
let colorArr = new Array(V);
for (let i = 0; i < V; ++i)
colorArr[i] = -1;
// One by one check all not yet colored vertices.
for (let i = 0; i < V; i++)
if (colorArr[i] == -1)
if (isBipartiteUtil(G, i, colorArr) == false)
return false;
return true;
}
// Returns true if G can be divided into
// two Cliques, else false.
function canBeDividedinTwoCliques(G)
{
// Find complement of G[][]
// All values are complemented except
// diagonal ones
let GC = new Array(V).fill(0).map(()=>new Array(V));
for (let i=0; i<V; i++)
for (let j=0; j<V; j++)
GC[i][j] = (i != j)? !G[i][j] : 0;
// Return true if complement is Bipartite
// else false.
return isBipartite(GC);
}
// Driver program to test above function
let G =[[0, 1, 1, 1, 0],
[1, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 1, 0, 0, 1],
[0, 0, 0, 1, 0]
];
canBeDividedinTwoCliques(G) ? document.write("Yes"):
document.write("No");
// This code is contributed by shinjanpatra
</script>
Producción :
Yes
La complejidad temporal de la implementación anterior es O(V 2 ).
Referencia:
http://math.stackexchange.com/questions/310092/the-two-clique-problem-is-in-p-or-np-p-np-for-hypothesis
Este artículo es una contribución de Shubham Saxena . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA