Problema de emparejamiento de amigos

Posted on by Rudeus Greyrat

Dados n amigos, cada uno puede permanecer soltero o emparejarse con algún otro amigo. Cada amigo puede emparejarse solo una vez. Averigüe el número total de formas en que los amigos pueden permanecer solteros o formar parejas. 

Ejemplos: 

Input  : n = 3
Output : 4
Explanation:
{1}, {2}, {3} : all single
{1}, {2, 3} : 2 and 3 paired but 1 is single.
{1, 2}, {3} : 1 and 2 are paired but 3 is single.
{1, 3}, {2} : 1 and 3 are paired but 2 is single.
Note that {1, 2} and {2, 1} are considered same.

Mathematical Explanation:
The problem is simplified version of how many ways we can divide n elements into multiple groups.
(here group size will be max of 2 elements).
In case of n = 3, we have only 2 ways to make a group: 
    1) all elements are individual(1,1,1)
    2) a pair and individual (2,1)
In case of n = 4, we have 3 ways to form a group:
    1) all elements are individual (1,1,1,1)
    2) 2 individuals and one pair (2,1,1)
    3) 2 separate pairs (2,2)

\tiny\textbf{Mathematical formula:} \newline{\frac{n!}{((g_1!)^x\times (g_2!)^y\times ... (g_n!)^z)\times(x!\times y!\times...z!)}}\space\space\tiny\text{ ----- (1)} \newline{\tiny\text{if same group size is repeated x,y,...,z times we have to divide additionally our answer by x!,y!...z!}} \newline{\tiny\text{now lets consider our case n=3 and group size max of size 2 and min size 1:}} \newline{\frac{3!}{(1!)^3\times(3!)} \space+\space \frac{3!}{(2!)^1\times(1!)^1\times(1!)^2}\space = 4} \newline{\text{now lets consider our case n=4:}} \newline{\frac{4!}{(1!)^4\times(4!)} \space+ \frac{4!}{(2!)^1\times(1!)^2\times(2!)}\space + \space \frac{4!}{(2!)^2\times(2!)}\space = 10}

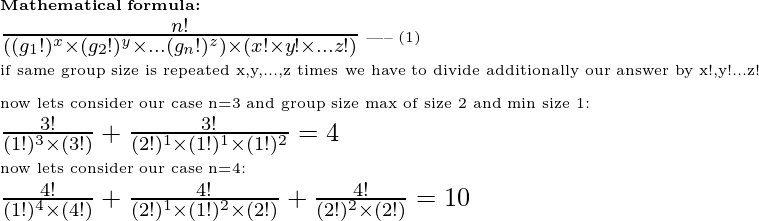
o emparejarse. Para la n-ésima persona hay dos opciones: 1) la n-ésima persona permanece soltera, recurrimos para f(n – 1) 2) la n-ésima persona se empareja con cualquiera de las n – 1 personas restantes. Obtenemos (n – 1) * f (n – 2) Por lo tanto, podemos escribir recursivamente f (n) como: f (n) = f (n – 1) + (n – 1) * f (n – 2)

Dado que la fórmula recursiva anterior tiene subproblemas superpuestos , podemos resolverlo usando Programación Dinámica.  

C++

// C++ program for solution of
// friends pairing problem
#include <bits/stdc++.h>
using namespace std;
 
// Returns count of ways n people
// can remain single or paired up.
int countFriendsPairings(int n)
{
    int dp[n + 1];
 
    // Filling dp[] in bottom-up manner using
    // recursive formula explained above.
    for (int i = 0; i <= n; i++) {
        if (i <= 2)
            dp[i] = i;
        else
            dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
    }
 
    return dp[n];
}
 
// Driver code
int main()
{
    int n = 4;
    cout << countFriendsPairings(n) << endl;
    return 0;
}

Java

// Java program for solution of
// friends pairing problem
import java.io.*;
 
class GFG {
 
    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        int dp[] = new int[n + 1];
 
        // Filling dp[] in bottom-up manner using
        // recursive formula explained above.
        for (int i = 0; i <= n; i++) {
            if (i <= 2)
                dp[i] = i;
            else
                dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
        }
 
        return dp[n];
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 4;
        System.out.println(countFriendsPairings(n));
    }
}
 
// This code is contributed by vt_m

Python3

# Python program solution of
# friends pairing problem
 
# Returns count of ways
# n people can remain
# single or paired up.
def countFriendsPairings(n):
 
    dp = [0 for i in range(n + 1)]
 
    # Filling dp[] in bottom-up manner using
    # recursive formula explained above.
    for i in range(n + 1):
 
        if(i <= 2):
            dp[i] = i
        else:
            dp[i] = dp[i - 1] + (i - 1) * dp[i - 2]
 
    return dp[n]
 
# Driver code
n = 4
print(countFriendsPairings(n))
 
# This code is contributed
# by Soumen Ghosh.

C#

// C# program solution for
// friends pairing problem
using System;
 
class GFG {
 
    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        int[] dp = new int[n + 1];
 
        // Filling dp[] in bottom-up manner using
        // recursive formula explained above.
        for (int i = 0; i <= n; i++) {
            if (i <= 2)
                dp[i] = i;
            else
                dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
        }
 
        return dp[n];
    }
 
    // Driver code
    public static void Main()
    {
        int n = 4;
        Console.Write(countFriendsPairings(n));
    }
}
 
// This code is contributed by nitin mittal.

PHP

<?php
// PHP program solution for
// friends pairing problem
 
// Returns count of ways n people
// can remain single or paired up.
function countFriendsPairings($n)
{
    $dp[$n + 1] = 0;
 
    // Filling dp[] in bottom-up
    // manner using recursive formula
    // explained above.
    for ($i = 0; $i <= $n; $i++)
    {
        if ($i <= 2)
        $dp[$i] = $i;
        else
        $dp[$i] = $dp[$i - 1] +
                     ($i - 1) *
                   $dp[$i - 2];
    }
 
    return $dp[$n];
}
 
// Driver code
$n = 4;
echo countFriendsPairings($n) ;
     
// This code is contributed
// by nitin mittal.
?>

Javascript

<script>
 
// Javascript program for solution of
// friends pairing problem
   
  
// Returns count of ways n people
    // can remain single or paired up.
    function countFriendsPairings(n)
    {
        let dp = [];
  
        // Filling dp[] in bottom-up manner using
        // recursive formula explained above.
        for (let i = 0; i <= n; i++) {
            if (i <= 2)
                dp[i] = i;
            else
                dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
        }
  
        return dp[n];
    }
        
 
// Driver Code
     
        let n = 4;
        document.write(countFriendsPairings(n));
 
</script>

Producción: 

10

Complejidad de tiempo: O(n) 
Espacio auxiliar: O(n)
Otro enfoque: (usando la recursividad)  

C++

// C++ program for solution of friends
// pairing problem Using Recursion
#include <bits/stdc++.h>
using namespace std;
 
int dp[1000];
 
// Returns count of ways n people
// can remain single or paired up.
int countFriendsPairings(int n)
{
    if (dp[n] != -1)
        return dp[n];
 
    if (n > 2)
        return dp[n] = countFriendsPairings(n - 1) + (n - 1) * countFriendsPairings(n - 2);
    else
        return dp[n] = n;
}
 
// Driver code
int main()
{
    memset(dp, -1, sizeof(dp));
    int n = 4;
    cout << countFriendsPairings(n) << endl;
    // this code is contributed by Kushdeep Mittal
}

Java

// Java program for solution of friends
// pairing problem Using Recursion
 
class GFG {
    static int[] dp = new int[1000];
 
    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        if (dp[n] != -1)
            return dp[n];
 
        if (n > 2)
            return dp[n] = countFriendsPairings(n - 1) + (n - 1) * countFriendsPairings(n - 2);
        else
            return dp[n] = n;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        for (int i = 0; i < 1000; i++)
            dp[i] = -1;
        int n = 4;
        System.out.println(countFriendsPairings(n));
    }
}
 
// This code is contributed by Ita_c.

Python3

# Python3 program for solution of friends
# pairing problem Using Recursion
dp = [-1] * 1000
# Returns count of ways n people
# can remain single or paired up.
def countFriendsPairings(n):
    global dp
     
    if(dp[n] != -1):
        return dp[n]
 
    if(n > 2):
 
        dp[n] = (countFriendsPairings(n - 1) +
                (n - 1) * countFriendsPairings(n - 2))
        return dp[n]
 
    else:
        dp[n] = n
        return dp[n]
     
# Driver Code
n = 4
print(countFriendsPairings(n))
 
# This code contributed by PrinciRaj1992

C#

// C# program for solution of friends
// pairing problem Using Recursion
using System;
 
class GFG {
    static int[] dp = new int[1000];
 
    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        if (dp[n] != -1)
            return dp[n];
 
        if (n > 2)
            return dp[n] = countFriendsPairings(n - 1) + (n - 1) * countFriendsPairings(n - 2);
        else
            return dp[n] = n;
    }
 
    // Driver code
    static void Main()
    {
        for (int i = 0; i < 1000; i++)
            dp[i] = -1;
        int n = 4;
        Console.Write(countFriendsPairings(n));
    }
}
 
// This code is contributed by DrRoot_

PHP

<?php
// PHP program for solution of friends
// pairing problem Using Recursion
 
// Returns count of ways n people
// can remain single or paired up.
function countFriendsPairings($n)
{
    $dp = array_fill(0, 1000, -1);
     
    if($dp[$n] != -1)
    return $dp[$n];
 
    if($n > 2)
    {
        $dp[$n] = countFriendsPairings($n - 1) + ($n - 1) *
                  countFriendsPairings($n - 2);
        return $dp[$n];
    }
    else
    {
        $dp[$n] = $n;
        return $dp[$n];
    }
}
     
// Driver Code
$n = 4;
echo countFriendsPairings($n)
 
// This code is contributed by Ryuga
?>

Javascript

<script>
 
// Javascript program for solution of friends
// pairing problem Using Recursion
     
    let dp = new Array(1000);
     
    // Returns count of ways n people
    // can remain single or paired up.
    function countFriendsPairings(n)
    {
        if (dp[n] != -1)
            return dp[n];
  
        if (n > 2)
            return dp[n] = countFriendsPairings(n - 1)
            + (n - 1) * countFriendsPairings(n - 2);
        else
            return dp[n] = n;
    }
     
    // Driver code
    for (let i = 0; i < 1000; i++)
        dp[i] = -1;
    let n = 4;
    document.write(countFriendsPairings(n));
     
    // This code is contributed by rag2127
     
</script>

Producción:

10

Complejidad de tiempo: O(n) 
Espacio auxiliar: O(n)
Dado que la fórmula anterior es similar al número de Fibonacci , podemos optimizar el espacio con una solución iterativa.  

C++

#include <bits/stdc++.h>
using namespace std;
 
// Returns count of ways n people
// can remain single or paired up.
int countFriendsPairings(int n)
{
    int a = 1, b = 2, c = 0;
    if (n <= 2) {
        return n;
    }
    for (int i = 3; i <= n; i++) {
        c = b + (i - 1) * a;
        a = b;
        b = c;
    }
    return c;
}
 
// Driver code
int main()
{
    int n = 4;
    cout << countFriendsPairings(n);
    return 0;
}
 
// This code is contributed by mits

Java

class GFG {
    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        int a = 1, b = 2, c = 0;
        if (n <= 2) {
            return n;
        }
        for (int i = 3; i <= n; i++) {
            c = b + (i - 1) * a;
            a = b;
            b = c;
        }
        return c;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 4;
        System.out.println(countFriendsPairings(n));
    }
}
 
// This code is contributed by Ravi Kasha.

Python3

# Returns count of ways n people
# can remain single or paired up.
def countFriendsPairings(n):
    a, b, c = 1, 2, 0;
    if (n <= 2):
        return n;
    for i in range(3, n + 1):
        c = b + (i - 1) * a;
        a = b;
        b = c;
    return c;
 
# Driver code
n = 4;
print(countFriendsPairings(n));
 
# This code contributed by Rajput-Ji

C#

using System;
 
class GFG {
    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        int a = 1, b = 2, c = 0;
        if (n <= 2) {
            return n;
        }
        for (int i = 3; i <= n; i++) {
            c = b + (i - 1) * a;
            a = b;
            b = c;
        }
        return c;
    }
 
    // Driver code
    public static void Main(String[] args)
    {
        int n = 4;
        Console.WriteLine(countFriendsPairings(n));
    }
}
 
// This code has been contributed by 29AjayKumar

PHP

<?php
    // Returns count of ways n people
    // can remain single or paired up.
    function countFriendsPairings($n)
    {
        $a = 1;
        $b = 2;
        $c = 0;
        if ($n <= 2)
        {
            return $n;
        }
        for ($i = 3; $i <= $n; $i++)
        {
            $c = $b + ($i - 1) * $a;
            $a = $b;
            $b = $c;
        }
        return $c;
    }
 
    // Driver code
        $n = 4;
        print(countFriendsPairings($n));
 
// This code is contributed by mits
?>

Javascript

<script>
    // Returns count of ways n people
    // can remain single or paired up.
    function countFriendsPairings(n)
    {
        let a = 1, b = 2, c = 0;
        if (n <= 2) {
            return n;
        }
        for (let i = 3; i <= n; i++) {
            c = b + (i - 1) * a;
            a = b;
            b = c;
        }
        return c;
    }
     
    // Driver code
    let n = 4;
    document.write(countFriendsPairings(n));
     
     
    // This code is contributed by avanitrachhadiya2155
</script>

Producción: 

10

Tiempo Complejidad : O(n) 
Espacio Auxiliar : O(1)

Otro enfoque: dado que podemos resolver el problema anterior usando matemáticas, la solución a continuación se realiza sin usar programación dinámica.

C++

// C++ soln using mathematical approach
#include <bits/stdc++.h>
using namespace std;
 
void preComputeFact(vector<long long int>& fact, int n)
{
    for(int i = 1; i <= n; i++)
        fact.push_back(fact[i - 1] * i);
}
 
// Returns count of ways n people
// can remain single or paired up.
int countFriendsPairings(vector<long long int> fact,
                         int n)
{
    int ones = n, twos = 1, ans = 0;
     
    while (ones >= 0)
    {
         
        // pow of 1 will always be one
        ans += fact[n] / (twos * fact[ones] *
               fact[(n - ones) / 2]);
        ones -= 2;
        twos *= 2;
    }
    return ans;
}
 
// Driver code
int main()
{
    vector<long long int> fact;
    fact.push_back(1);
 
    preComputeFact(fact, 100);
    int n = 4;
 
    cout << countFriendsPairings(fact, n) << endl;
    return 0;
}
 
// This code is contributed by rajsanghavi9.

Java

// Java soln using mathematical approach
import java.util.*;
 
class GFG{
static   Vector<Integer> fact;
static void preComputeFact( int n)
{
    for(int i = 1; i <= n; i++)
        fact.add(fact.elementAt(i - 1) * i);
}
 
// Returns count of ways n people
// can remain single or paired up.
static int countFriendsPairings(int n)
{
    int ones = n, twos = 1, ans = 0;
     
    while (ones >= 0)
    {
         
        // pow of 1 will always be one
        ans += fact.elementAt(n) / (twos * fact.elementAt(ones) *
               fact.elementAt((n - ones) / 2));
        ones -= 2;
        twos *= 2;
    }
    return ans;
}
 
// Driver code
public static void main(String[] args)
{
  fact = new Vector<>();
    fact.add(1);
 
    preComputeFact(100);
    int n = 4;
 
    System.out.print(countFriendsPairings(n) +"\n");
}
}
 
// This code is contributed by umadevi9616

Python3

# Python3 soln using mathematical approach
# factorial array is stored dynamically
fact = [1]
def preComputeFact(n):
    for i in range(1, n+1):
        fact.append((fact[i-1]*i))
 
# Returns count of ways n people
# can remain single or paired up.
def countFriendsPairings(n):
    ones = n
    twos = 1
    ans = 0
    while(ones >= 0):
        # pow of 1 will always be one
        ans = ans + (fact[n]//(twos*fact[ones]*fact[(n-ones)//2]))
        ones = ones - 2
        twos = twos * 2
    return(ans)
 
 
# Driver Code
# pre-compute factorial
preComputeFact(1000)
n = 4
print(countFriendsPairings(n))
 
# solution contributed by adarsh_007

C#

// C# program to implement the approach
using System;
using System.Collections.Generic;
public class GFG
{
 
  // initializing the fact list
  static List<int> fact = new List<int>();
 
  // computing the next n values of fact
  static void preComputeFact(int n)
  {
    for (int i = 1; i <= n; i++) {
      fact.Add(fact[i - 1] * i);
    }
  }
 
  // Returns count of ways n people
  // can remain single or paired up.
  static int countFriendsPairings(int n)
  {
    int ones = n;
    int twos = 1;
    int ans = 0;
 
    while (ones >= 0) {
 
      // pow of 1 will always be one
      ans += fact[n]
        / (twos * fact[ones]
           * fact[(n - ones) / 2]);
      ones -= 2;
      twos *= 2;
    }
    return ans;
  }
 
  // driver code
  static public void Main()
  {
 
    // initializing the first element of fact
    fact.Add(1);
    preComputeFact(100);
    int n = 4;
    Console.Write(countFriendsPairings(n));
  }
}
 
// this code is contributed by phasing17

Javascript

<script>
 
// Javascript soln using mathematical approach
// factorial array is stored dynamically
 
let fact = [1];
 
function preComputeFact(n)
{
    for(let i=1;i<n+1;i++)
    {
        fact.push((fact[i-1]*i));
    }
}
 
// Returns count of ways n people
// can remain single or paired up.
function countFriendsPairings(n)
{
    let ones = n
    let twos = 1;
    let ans = 0;
    while(ones >= 0)
    {
         // pow of 1 will always be one
        ans = ans + Math.floor(fact[n]/(twos*fact[ones]*
        fact[(n-ones)/2]))
        ones = ones - 2
        twos = twos * 2
    }
    return ans;
}
 
// Driver Code
// pre-compute factorial
preComputeFact(1000)
n = 4
document.write(countFriendsPairings(n))
 
// This code is contributed by ab2127
 
</script>

Producción:

10

Complejidad temporal:  O(n) 
Espacio auxiliar: O(n)

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *