Dado un tablero por n donde n es de forma 2 k donde k >= 1 (Básicamente, n es una potencia de 2 con un valor mínimo de 2). Al tablero le falta una celda (de tamaño 1 x 1). Rellena el tablero con fichas en forma de L. El mosaico en forma de AL es un cuadrado de 2 x 2 al que le falta una celda de tamaño 1×1.
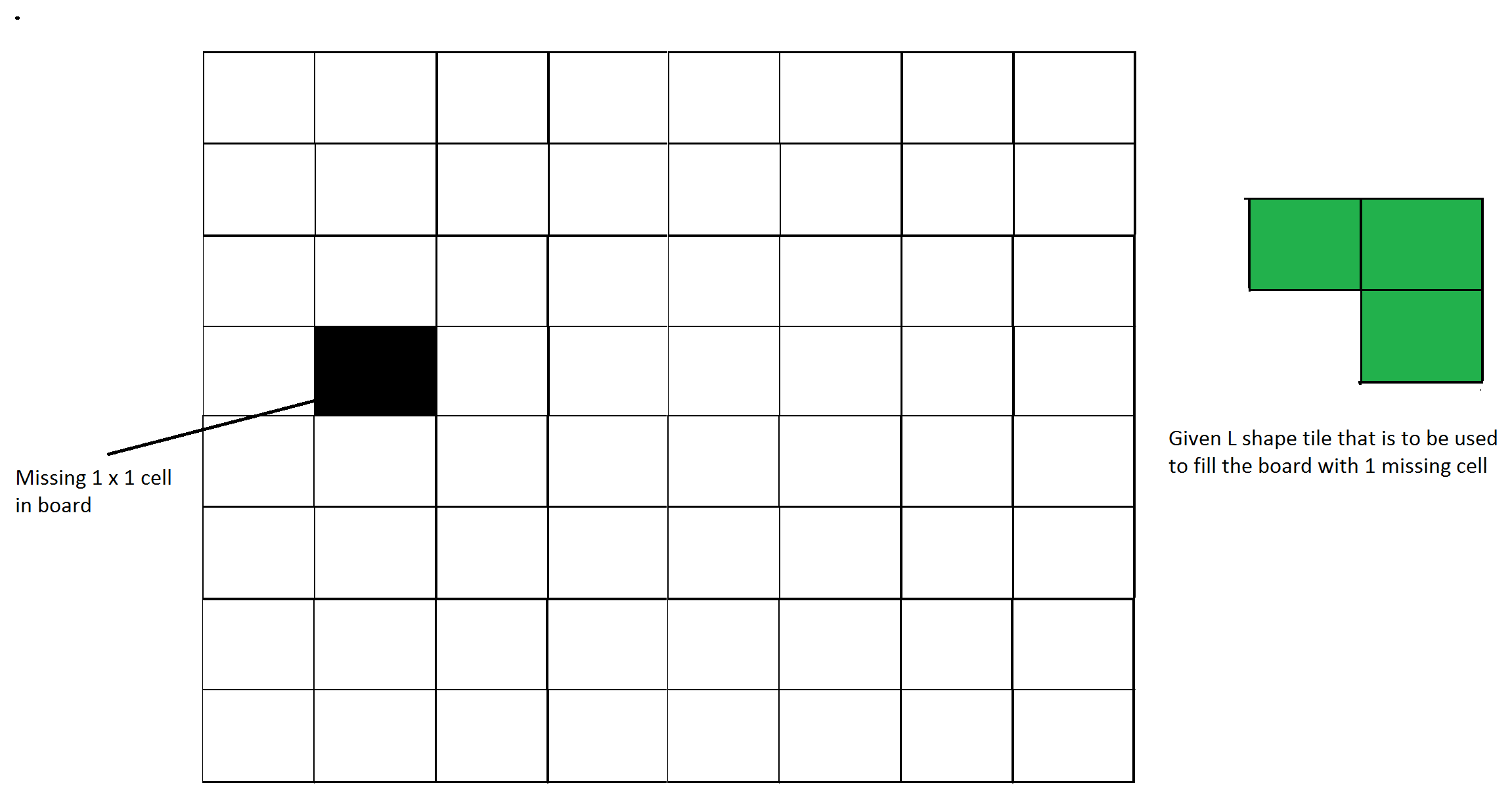
Figura 1: Una entrada de ejemplo
Este problema se puede resolver usando Divide and Conquer. A continuación se muestra el algoritmo recursivo.
// n is size of given square, p is location of missing cell Tile(int n, Point p) 1) Base case: n = 2, A 2 x 2 square with one cell missing is nothing but a tile and can be filled with a single tile. 2) Place a L shaped tile at the center such that it does not cover the n/2 * n/2 subsquare that has a missing square. Now all four subsquares of size n/2 x n/2 have a missing cell (a cell that doesn't need to be filled). See figure 2 below. 3) Solve the problem recursively for following four. Let p1, p2, p3 and p4 be positions of the 4 missing cells in 4 squares. a) Tile(n/2, p1) b) Tile(n/2, p2) c) Tile(n/2, p3) d) Tile(n/2, p3)
Los siguientes diagramas muestran el funcionamiento del algoritmo anterior.
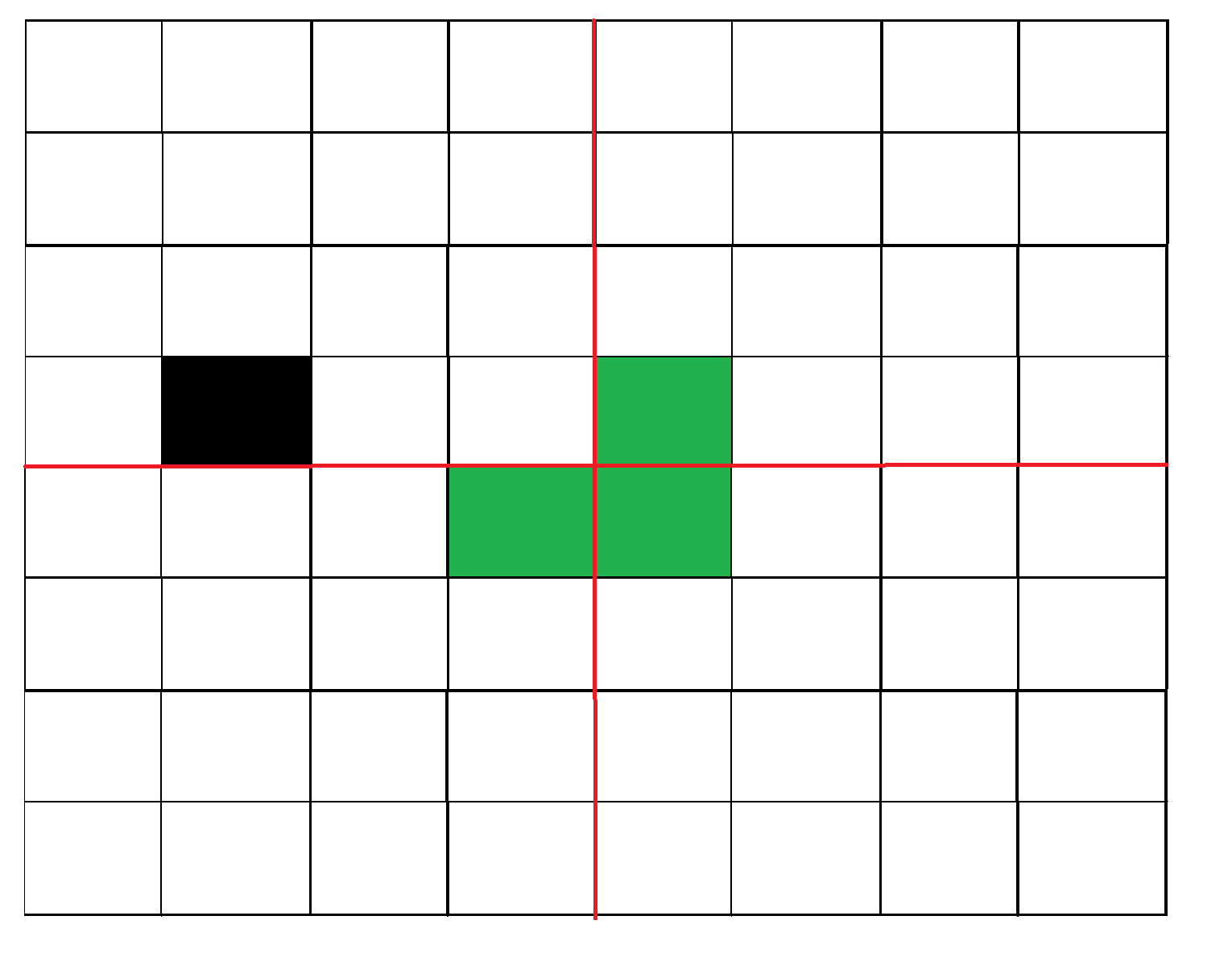
Figura 2: Después de colocar la primera loseta
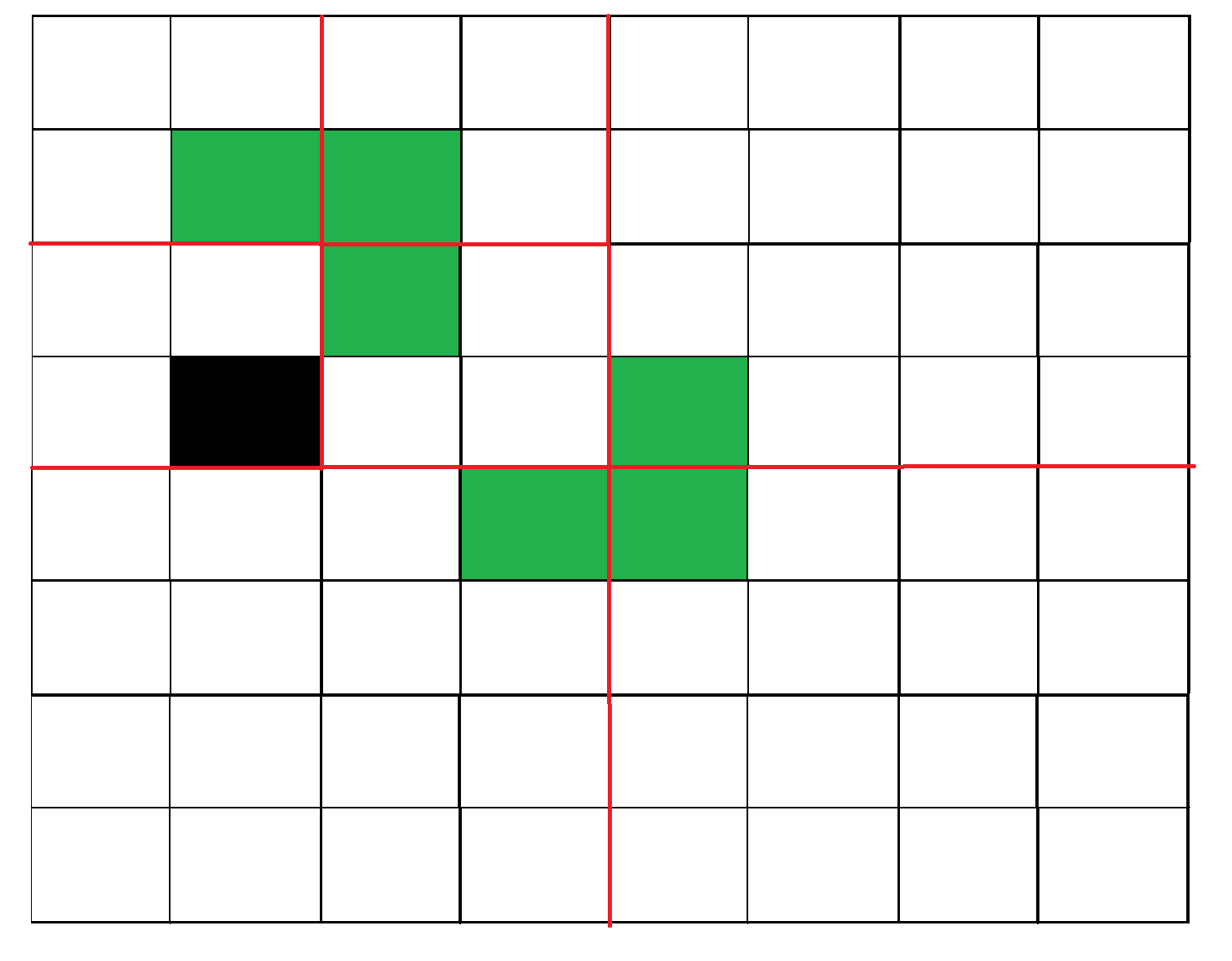
Figura 3: Recurrente para el primer subcuadrado.
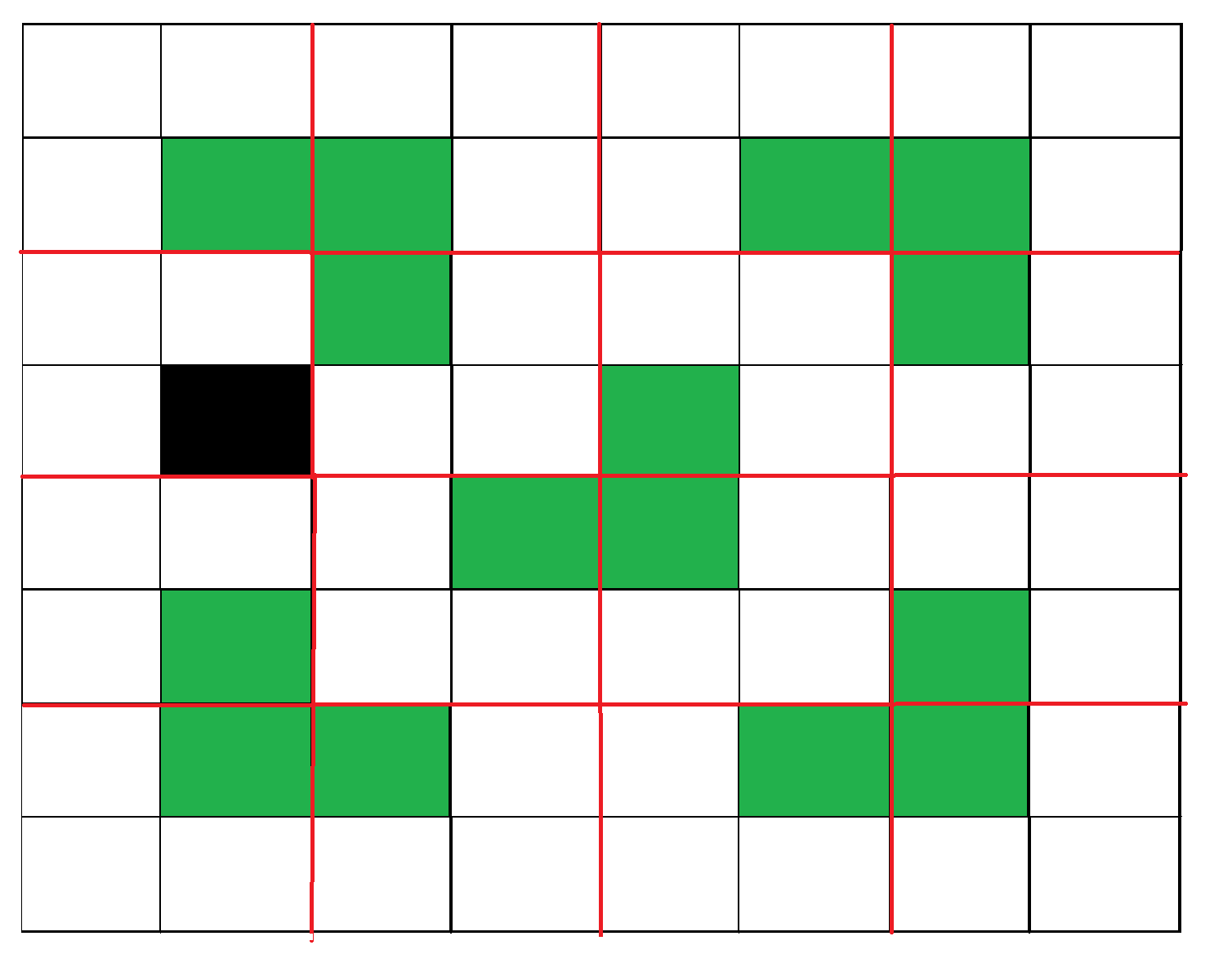
Figura 4: Muestra el primer paso en los cuatro subcuadrados.
Ejemplos:
Input : size = 2 and mark coordinates = (0, 0) Output : -1 1 1 1 Coordinate (0, 0) is marked. So, no tile is there. In the remaining three positions, a tile is placed with its number as 1. Input : size = 4 and mark coordinates = (0, 0) Output : -1 3 2 2 3 3 1 2 4 1 1 5 4 4 5 5
A continuación se muestra la implementación de la idea anterior:
C++
// C++ program to place tiles
#include <bits/stdc++.h>
using namespace std;
int size_of_grid, b, a, cnt = 0;
int arr[128][128];
// Placing tile at the given coordinates
void place(int x1, int y1, int x2,
int y2, int x3, int y3)
{
cnt++;
arr[x1][y1] = cnt;
arr[x2][y2] = cnt;
arr[x3][y3] = cnt;
}
// Quadrant names
// 1 2
// 3 4
// Function based on divide and conquer
int tile(int n, int x, int y)
{
int r, c;
if (n == 2) {
cnt++;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (arr[x + i][y + j] == 0) {
arr[x + i][y + j] = cnt;
}
}
}
return 0;
}
// finding hole location
for (int i = x; i < x + n; i++) {
for (int j = y; j < y + n; j++) {
if (arr[i][j] != 0)
r = i, c = j;
}
}
// If missing tile is 1st quadrant
if (r < x + n / 2 && c < y + n / 2)
place(x + n / 2, y + (n / 2) - 1, x + n / 2,
y + n / 2, x + n / 2 - 1, y + n / 2);
// If missing Tile is in 3rd quadrant
else if (r >= x + n / 2 && c < y + n / 2)
place(x + (n / 2) - 1, y + (n / 2), x + (n / 2),
y + n / 2, x + (n / 2) - 1, y + (n / 2) - 1);
// If missing Tile is in 2nd quadrant
else if (r < x + n / 2 && c >= y + n / 2)
place(x + n / 2, y + (n / 2) - 1, x + n / 2,
y + n / 2, x + n / 2 - 1, y + n / 2 - 1);
// If missing Tile is in 4th quadrant
else if (r >= x + n / 2 && c >= y + n / 2)
place(x + (n / 2) - 1, y + (n / 2), x + (n / 2),
y + (n / 2) - 1, x + (n / 2) - 1,
y + (n / 2) - 1);
// dividing it again in 4 quadrants
tile(n / 2, x, y + n / 2);
tile(n / 2, x, y);
tile(n / 2, x + n / 2, y);
tile(n / 2, x + n / 2, y + n / 2);
return 0;
}
// Driver program to test above function
int main()
{
// size of box
size_of_grid = 8;
memset(arr, 0, sizeof(arr));
// Coordinates which will be marked
a = 0, b = 0;
// Here tile can not be placed
arr[a][b] = -1;
tile(size_of_grid, 0, 0);
// The grid is
for (int i = 0; i < size_of_grid; i++) {
for (int j = 0; j < size_of_grid; j++)
cout << arr[i][j] << " \t";
cout << "\n";
}
}
Java
// Java program to place tiles
public class GFG
{
static int size_of_grid, b, a, cnt = 0;
static int[][] arr = new int[128][128];
// Placing tile at the given coordinates
static void place(int x1, int y1, int x2,
int y2, int x3, int y3)
{
cnt++;
arr[x1][y1] = cnt;
arr[x2][y2] = cnt;
arr[x3][y3] = cnt;
}
// Quadrant names
// 1 2
// 3 4
// Function based on divide and conquer
static int tile(int n, int x, int y)
{
int r = 0, c = 0;
if (n == 2)
{
cnt++;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (arr[x + i][y + j] == 0)
{
arr[x + i][y + j] = cnt;
}
}
}
return 0;
}
// finding hole location
for (int i = x; i < x + n; i++)
{
for (int j = y; j < y + n; j++)
{
if (arr[i][j] != 0)
{
r = i;
c = j;
}
}
}
// If missing tile is 1st quadrant
if (r < x + n / 2 && c < y + n / 2)
place(x + n / 2, y + (n / 2) - 1, x + n / 2,
y + n / 2, x + n / 2 - 1, y + n / 2);
// If missing Tile is in 3rd quadrant
else if (r >= x + n / 2 && c < y + n / 2)
place(x + (n / 2) - 1, y + (n / 2), x + (n / 2),
y + n / 2, x + (n / 2) - 1, y + (n / 2) - 1);
// If missing Tile is in 2nd quadrant
else if (r < x + n / 2 && c >= y + n / 2)
place(x + n / 2, y + (n / 2) - 1, x + n / 2,
y + n / 2, x + n / 2 - 1, y + n / 2 - 1);
// If missing Tile is in 4th quadrant
else if (r >= x + n / 2 && c >= y + n / 2)
place(x + (n / 2) - 1, y + (n / 2), x + (n / 2),
y + (n / 2) - 1, x + (n / 2) - 1,
y + (n / 2) - 1);
// dividing it again in 4 quadrants
tile(n / 2, x, y + n / 2);
tile(n / 2, x, y);
tile(n / 2, x + n / 2, y);
tile(n / 2, x + n / 2, y + n / 2);
return 0;
}
// Driver code
public static void main(String[] args)
{
// size of box
size_of_grid = 8;
// Coordinates which will be marked
a = 0; b = 0;
// Here tile can not be placed
arr[a][b] = -1;
tile(size_of_grid, 0, 0);
// The grid is
for (int i = 0; i < size_of_grid; i++)
{
for (int j = 0; j < size_of_grid; j++)
System.out.print(arr[i][j] + " ");
System.out.println();;
}
}
}
// This code is contributed by divyeshrabadiya07.
C#
// C# program to place tiles
using System;
class GFG
{
static int size_of_grid, b, a, cnt = 0;
static int[,] arr = new int[128, 128];
// Placing tile at the given coordinates
static void place(int x1, int y1, int x2,
int y2, int x3, int y3)
{
cnt++;
arr[x1, y1] = cnt;
arr[x2, y2] = cnt;
arr[x3, y3] = cnt;
}
// Quadrant names
// 1 2
// 3 4
// Function based on divide and conquer
static int tile(int n, int x, int y)
{
int r = 0, c = 0;
if (n == 2)
{
cnt++;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (arr[x + i, y + j] == 0)
{
arr[x + i, y + j] = cnt;
}
}
}
return 0;
}
// finding hole location
for (int i = x; i < x + n; i++)
{
for (int j = y; j < y + n; j++)
{
if (arr[i, j] != 0)
{
r = i;
c = j;
}
}
}
// If missing tile is 1st quadrant
if (r < x + n / 2 && c < y + n / 2)
place(x + n / 2, y + (n / 2) - 1, x + n / 2,
y + n / 2, x + n / 2 - 1, y + n / 2);
// If missing Tile is in 3rd quadrant
else if (r >= x + n / 2 && c < y + n / 2)
place(x + (n / 2) - 1, y + (n / 2), x + (n / 2),
y + n / 2, x + (n / 2) - 1, y + (n / 2) - 1);
// If missing Tile is in 2nd quadrant
else if (r < x + n / 2 && c >= y + n / 2)
place(x + n / 2, y + (n / 2) - 1, x + n / 2,
y + n / 2, x + n / 2 - 1, y + n / 2 - 1);
// If missing Tile is in 4th quadrant
else if (r >= x + n / 2 && c >= y + n / 2)
place(x + (n / 2) - 1, y + (n / 2), x + (n / 2),
y + (n / 2) - 1, x + (n / 2) - 1,
y + (n / 2) - 1);
// dividing it again in 4 quadrants
tile(n / 2, x, y + n / 2);
tile(n / 2, x, y);
tile(n / 2, x + n / 2, y);
tile(n / 2, x + n / 2, y + n / 2);
return 0;
}
// Driver code
static void Main()
{
// size of box
size_of_grid = 8;
// Coordinates which will be marked
a = 0; b = 0;
// Here tile can not be placed
arr[a, b] = -1;
tile(size_of_grid, 0, 0);
// The grid is
for (int i = 0; i < size_of_grid; i++)
{
for (int j = 0; j < size_of_grid; j++)
Console.Write(arr[i,j] + " ");
Console.WriteLine();
}
}
}
// This code is contributed by divyesh072019.
Python3
# Python3 program to place tiles size_of_grid = 0 b = 0 a = 0 cnt = 0 arr = [[0 for i in range(128)] for j in range(128)] def place(x1, y1, x2, y2, x3, y3): global cnt cnt += 1 arr[x1][y1] = cnt; arr[x2][y2] = cnt; arr[x3][y3] = cnt; def tile(n, x, y): global cnt r = 0 c = 0 if (n == 2): cnt += 1 for i in range(n): for j in range(n): if(arr[x + i][y + j] == 0): arr[x + i][y + j] = cnt return 0; for i in range(x, x + n): for j in range(y, y + n): if (arr[i][j] != 0): r = i c = j if (r < x + n / 2 and c < y + n / 2): place(x + int(n / 2), y + int(n / 2) - 1, x + int(n / 2), y + int(n / 2), x + int(n / 2) - 1, y + int(n / 2)) elif(r >= x + int(n / 2) and c < y + int(n / 2)): place(x + int(n / 2) - 1, y + int(n / 2), x + int(n / 2), y + int(n / 2), x + int(n / 2) - 1, y + int(n / 2) - 1) elif(r < x + int(n / 2) and c >= y + int(n / 2)): place(x + int(n / 2), y + int(n / 2) - 1, x + int(n / 2), y + int(n / 2), x + int(n / 2) - 1, y + int(n / 2) - 1) elif(r >= x + int(n / 2) and c >= y + int(n / 2)): place(x + int(n / 2) - 1, y + int(n / 2), x + int(n / 2), y + int(n / 2) - 1, x + int(n / 2) - 1, y + int(n / 2) - 1) tile(int(n / 2), x, y + int(n / 2)); tile(int(n / 2), x, y); tile(int(n / 2), x + int(n / 2), y); tile(int(n / 2), x + int(n / 2), y + int(n / 2)); return 0 size_of_grid = 8 a = 0 b = 0 arr[a][b] = -1 tile(size_of_grid, 0, 0) for i in range(size_of_grid): for j in range(size_of_grid): print(arr[i][j], end=" ") print() # This code is contributed by rag2127
Javascript
<script>
// Javascript program to place tiles
var size_of_grid, b, a, cnt = 0;
var arr = Array.from(Array(128), ()=>Array(128).fill(0));
// Placing tile at the given coordinates
function place(x1, y1, x2, y2, x3, y3)
{
cnt++;
arr[x1][y1] = cnt;
arr[x2][y2] = cnt;
arr[x3][y3] = cnt;
}
// Quadrant names
// 1 2
// 3 4
// Function based on divide and conquer
function tile(n, x, y)
{
var r, c;
if (n == 2) {
cnt++;
for (var i = 0; i < n; i++) {
for (var j = 0; j < n; j++) {
if (arr[x + i][y + j] == 0) {
arr[x + i][y + j] = cnt;
}
}
}
return 0;
}
// finding hole location
for (var i = x; i < x + n; i++) {
for (var j = y; j < y + n; j++) {
if (arr[i][j] != 0)
r = i, c = j;
}
}
// If missing tile is 1st quadrant
if (r < x + n / 2 && c < y + n / 2)
place(x + n / 2, y + (n / 2) - 1, x + n / 2,
y + n / 2, x + n / 2 - 1, y + n / 2);
// If missing Tile is in 3rd quadrant
else if (r >= x + n / 2 && c < y + n / 2)
place(x + (n / 2) - 1, y + (n / 2), x + (n / 2),
y + n / 2, x + (n / 2) - 1, y + (n / 2) - 1);
// If missing Tile is in 2nd quadrant
else if (r < x + n / 2 && c >= y + n / 2)
place(x + n / 2, y + (n / 2) - 1, x + n / 2,
y + n / 2, x + n / 2 - 1, y + n / 2 - 1);
// If missing Tile is in 4th quadrant
else if (r >= x + n / 2 && c >= y + n / 2)
place(x + (n / 2) - 1, y + (n / 2), x + (n / 2),
y + (n / 2) - 1, x + (n / 2) - 1,
y + (n / 2) - 1);
// dividing it again in 4 quadrants
tile(n / 2, x, y + n / 2);
tile(n / 2, x, y);
tile(n / 2, x + n / 2, y);
tile(n / 2, x + n / 2, y + n / 2);
return 0;
}
// Driver program to test above function
// size of box
size_of_grid = 8;
// Coordinates which will be marked
a = 0, b = 0;
// Here tile can not be placed
arr[a][b] = -1;
tile(size_of_grid, 0, 0);
// The grid is
for (var i = 0; i < size_of_grid; i++) {
for (var j = 0; j < size_of_grid; j++)
document.write(arr[i][j] + " ");
document.write("<br>");
}
// This code is contributed by rutvik_56.
</script>
-1 9 8 8 4 4 3 3 9 9 7 8 4 2 2 3 10 7 7 11 5 5 2 6 10 10 11 11 1 5 6 6 14 14 13 1 1 19 18 18 14 12 13 13 19 19 17 18 15 12 12 16 20 17 17 21 15 15 16 16 20 20 21 21
Complejidad del tiempo:
la relación de recurrencia para el algoritmo recursivo anterior se puede escribir de la siguiente manera. C es una constante.
T(n) = 4T(n/2) + C
La recursividad anterior se puede resolver usando el método maestro y la complejidad del tiempo es O(n 2 )
¿Como funciona esto?
El funcionamiento del algoritmo Divide and Conquer se puede probar mediante la inducción matemática. Sea el cuadrado de entrada de tamaño 2 k x 2 k donde k >=1.
Caso base: sabemos que el problema se puede resolver para k = 1. Tenemos un cuadrado de 2 x 2 al que le falta una celda.
Hipótesis de inducción: Deje que el problema se pueda resolver para k-1.
Ahora tenemos que demostrar que el problema se puede resolver para k si se puede resolver para k-1. Para k, colocamos un mosaico en forma de L en el medio y tenemos cuatro subcuadrados con una dimensión de 2 k-1 x 2 k-1 como se muestra en la figura 2 anterior. Entonces, si podemos resolver 4 subcuadrados, podemos resolver el cuadrado completo.
Referencias:
http://www.comp.nus.edu.sg/~sanjay/cs3230/dandc.pdf
Este artículo es una contribución de Abhay Rathi . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA