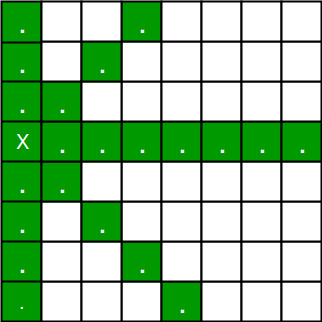
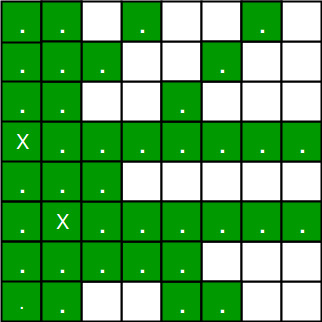
El rompecabezas de N reinas es el problema de colocar N reinas de ajedrez en un tablero de ajedrez N × N de modo que no haya dos reinas que se amenacen entre sí. Por lo tanto, una solución requiere que no haya dos reinas que compartan la misma fila, columna o diagonal.
El algoritmo de retroceso para N-Queen ya se analiza aquí . En la solución de retroceso, retrocedemos cuando llegamos a un callejón sin salida. En la solución Branch and Bound, después de construir una solución parcial, nos damos cuenta de que no tiene sentido profundizar más ya que vamos a llegar a un callejón sin salida .
Comencemos describiendo la solución de retroceso. “La idea es colocar las reinas una por una en diferentes columnas, comenzando desde la columna más a la izquierda. Cuando colocamos una reina en una columna, buscamos conflictos con reinas ya colocadas. En la columna actual, si encontramos una fila para la que no hay conflicto, marcamos esta fila y columna como parte de la solución. Si no encontramos esa fila debido a conflictos, retrocedemos y devolvemos falso”.
- Para la primera reina, hay un total de 8 posibilidades, ya que podemos colocar la primera reina en cualquier fila de la primera columna. Coloquemos la Reina 1 en la fila 3.
- Después de colocar la 1ra Reina, quedan 7 posibilidades para la 2da Reina. Pero espera, en realidad no tenemos 7 posibilidades. No podemos colocar a la Reina 2 en las filas 2, 3 o 4 ya que esas celdas están bajo el ataque de la Reina 1. Por lo tanto, a la Reina 2 solo le quedan 8 – 3 = 5 posiciones válidas.
- Después de elegir una posición para la Reina 2, la Reina 3 tiene aún menos opciones ya que la mayoría de las casillas de su columna están bajo el ataque de las primeras 2 Reinas.
Necesitamos encontrar una forma eficiente de realizar un seguimiento de las células que están siendo atacadas. En la solución anterior, mantuvimos una array booleana de 8 por 8 y la actualizamos cada vez que colocamos una reina, pero eso requería un tiempo lineal para actualizar, ya que necesitamos verificar celdas seguras.
Básicamente, tenemos que asegurarnos de 4 cosas:
1. No hay dos reinas compartiendo una columna.
2. No hay dos reinas que compartan una fila.
3. No hay dos reinas que compartan una diagonal superior derecha a izquierda inferior.
4. No hay dos reinas que compartan una diagonal superior izquierda a inferior derecha.
El número 1 es automático debido a la forma en que almacenamos la solución. Para los números 2, 3 y 4, podemos realizar actualizaciones en tiempo O(1). La idea es mantener tres arrays booleanas que nos digan qué filas y qué diagonales están ocupadas .
Primero hagamos un preprocesamiento. Vamos a crear dos arrays N x N, una para /diagonal y otra para \diagonal. Llamémoslos slashCode y backslashCode respectivamente. El truco es llenarlos de tal manera que dos reinas que comparten una misma /diagonal tendrán el mismo valor en matrix slashCode, y si comparten la misma \diagonal, tendrán el mismo valor en backslashCode matrix.
Para una array N x N, llene la array slashCode y backslashCode usando la siguiente fórmula:
slashCode[row][col] = row + col
backslashCode[row][col] = row – col + (N-1)
El uso de la fórmula anterior dará como resultado las arrays siguientes
La ‘N – 1’ en el código de barra invertida está ahí para garantizar que los códigos nunca sean negativos porque usaremos los códigos como índices en una array.
Ahora, antes de colocar la reina i en la fila j, primero verificamos si se usa la fila j (usar una array para almacenar la información de la fila). Luego verificamos si se usa el código de barra diagonal ( j + i ) o el código de barra invertida ( j – i + 7 ) (mantenga dos arrays que nos dirán qué diagonales están ocupadas). Si es así, entonces tenemos que probar una ubicación diferente para la reina i. De lo contrario, marcamos la fila y las dos diagonales como usadas y recurrimos a la reina i + 1. Después de que regrese la llamada recursiva y antes de intentar otra posición para la reina i, necesitamos restablecer la fila, el código de barra diagonal y el código de barra invertida como sin usar de nuevo, como en el código de las notas anteriores.
A continuación se muestra la implementación de la idea anterior:
Este código toma la entrada dinámica:
C++
#include<bits/stdc++.h>
using namespace std;
int N;
// function for printing the solution
void printSol(vector<vector<int>>board)
{
for(int i = 0;i<N;i++){
for(int j = 0;j<N;j++){
cout<<board[i][j]<<" ";
}
cout<<"\n";
}
}
/* Optimized isSafe function
isSafe function to check if current row contins or current left diagonal or current right diagonal contains any queen or not if
yes return false
else return true
*/
bool isSafe(int row ,int col ,vector<bool>rows , vector<bool>left_digonals ,vector<bool>Right_digonals)
{
if(rows[row] == true || left_digonals[row+col] == true || Right_digonals[col-row+N-1] == true){
return false;
}
return true;
}
// Recursive function to solve N-queen Problem
bool solve(vector<vector<int>>& board ,int col ,vector<bool>rows , vector<bool>left_digonals ,vector<bool>Right_digonals)
{
// base Case : If all Queens are placed
if(col>=N){
return true;
}
/* Consider this Column and move in all rows one by one */
for(int i = 0;i<N;i++)
{
if(isSafe(i,col,rows,left_digonals,Right_digonals) == true)
{
rows[i] = true;
left_digonals[i+col] = true;
Right_digonals[col-i+N-1] = true;
board[i][col] = 1; // placing the Queen in board[i][col]
/* recur to place rest of the queens */
if(solve(board,col+1,rows,left_digonals,Right_digonals) == true){
return true;
}
// Backtracking
rows[i] = false;
left_digonals[i+col] = false;
Right_digonals[col-i+N-1] = false;
board[i][col] = 0; // removing the Queen from board[i][col]
}
}
return false;
}
int main()
{
// Taking input from the user
cout<<"Enter the no of rows for the square Board : ";
cin>>N;
// board of size N*N
vector<vector<int>>board(N,vector<int>(N,0));
// array to tell which rows are occupied
vector<bool>rows(N,false);
// arrays to tell which diagonals are occupied
vector<bool>left_digonals(2*N-1,false);
vector<bool>Right_digonals(2*N-1,false);
bool ans = solve(board , 0, rows,left_digonals,Right_digonals);
if(ans == true){
// printing the solution Board
printSol(board);
}
else{
cout<<"Solution Does not Exist\n";
}
}
// This Code is Contributed by Parshant Rajput
C
/* C++ program to solve N Queen Problem using Branch
and Bound */
#include<stdio.h>
#include<string.h>
#include<stdbool.h>
#define N 8
/* A utility function to print solution */
void printSolution(int board[N][N])
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
printf("%2d ", board[i][j]);
printf("\n");
}
}
/* A Optimized function to check if a queen can
be placed on board[row][col] */
bool isSafe(int row, int col, int slashCode[N][N],
int backslashCode[N][N], bool rowLookup[],
bool slashCodeLookup[], bool backslashCodeLookup[] )
{
if (slashCodeLookup[slashCode[row][col]] ||
backslashCodeLookup[backslashCode[row][col]] ||
rowLookup[row])
return false;
return true;
}
/* A recursive utility function
to solve N Queen problem */
bool solveNQueensUtil(int board[N][N], int col,
int slashCode[N][N], int backslashCode[N][N],
bool rowLookup[N],
bool slashCodeLookup[],
bool backslashCodeLookup[] )
{
/* base case: If all queens are placed
then return true */
if (col >= N)
return true;
/* Consider this column and try placing
this queen in all rows one by one */
for (int i = 0; i < N; i++)
{
/* Check if queen can be placed on
board[i][col] */
if ( isSafe(i, col, slashCode,
backslashCode, rowLookup,
slashCodeLookup, backslashCodeLookup) )
{
/* Place this queen in board[i][col] */
board[i][col] = 1;
rowLookup[i] = true;
slashCodeLookup[slashCode[i][col]] = true;
backslashCodeLookup[backslashCode[i][col]] = true;
/* recur to place rest of the queens */
if ( solveNQueensUtil(board, col + 1,
slashCode, backslashCode,
rowLookup, slashCodeLookup, backslashCodeLookup) )
return true;
/* If placing queen in board[i][col]
doesn't lead to a solution, then backtrack */
/* Remove queen from board[i][col] */
board[i][col] = 0;
rowLookup[i] = false;
slashCodeLookup[slashCode[i][col]] = false;
backslashCodeLookup[backslashCode[i][col]] = false;
}
}
/* If queen can not be place in any row in
this column col then return false */
return false;
}
/* This function solves the N Queen problem using
Branch and Bound. It mainly uses solveNQueensUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
bool solveNQueens()
{
int board[N][N];
memset(board, 0, sizeof board);
// helper matrices
int slashCode[N][N];
int backslashCode[N][N];
// arrays to tell us which rows are occupied
bool rowLookup[N] = {false};
//keep two arrays to tell us
// which diagonals are occupied
bool slashCodeLookup[2*N - 1] = {false};
bool backslashCodeLookup[2*N - 1] = {false};
// initialize helper matrices
for (int r = 0; r < N; r++)
for (int c = 0; c < N; c++) {
slashCode[r] = r + c,
backslashCode[r] = r - c + 7;
}
if (solveNQueensUtil(board, 0,
slashCode, backslashCode,
rowLookup, slashCodeLookup, backslashCodeLookup) ==
false )
{
printf("Solution does not exist");
return false;
}
// solution found
printSolution(board);
return true;
}
// Driver program to test above function
int main()
{
solveNQueens();
return 0;
}
Java
// Java program to solve N Queen Problem
// using Branch and Bound
import java.io.*;
import java.util.Arrays;
class GFG{
static int N = 8;
// A utility function to print solution
static void printSolution(int board[][])
{
int N = board.length;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N; j++)
System.out.printf("%2d ", board[i][j]);
System.out.printf("\n");
}
}
// A Optimized function to check if a queen
// can be placed on board[row][col]
static boolean isSafe(int row, int col,
int slashCode[][],
int backslashCode[][],
boolean rowLookup[],
boolean slashCodeLookup[],
boolean backslashCodeLookup[])
{
if (slashCodeLookup[slashCode[row][col]] ||
backslashCodeLookup[backslashCode[row][col]] ||
rowLookup[row])
return false;
return true;
}
// A recursive utility function to
// solve N Queen problem
static boolean solveNQueensUtil(
int board[][], int col, int slashCode[][],
int backslashCode[][], boolean rowLookup[],
boolean slashCodeLookup[],
boolean backslashCodeLookup[])
{
// Base case: If all queens are placed
// then return true
int N = board.length;
if (col >= N)
return true;
// Consider this column and try placing
// this queen in all rows one by one
for(int i = 0; i < N; i++)
{
// Check if queen can be placed on board[i][col]
if (isSafe(i, col, slashCode, backslashCode,
rowLookup, slashCodeLookup,
backslashCodeLookup))
{
// Place this queen in board[i][col]
board[i][col] = 1;
rowLookup[i] = true;
slashCodeLookup[slashCode[i][col]] = true;
backslashCodeLookup[backslashCode[i][col]] = true;
// recur to place rest of the queens
if (solveNQueensUtil(
board, col + 1, slashCode,
backslashCode, rowLookup,
slashCodeLookup,
backslashCodeLookup))
return true;
// If placing queen in board[i][col] doesn't
// lead to a solution, then backtrack
// Remove queen from board[i][col]
board[i][col] = 0;
rowLookup[i] = false;
slashCodeLookup[slashCode[i][col]] = false;
backslashCodeLookup[backslashCode[i][col]] = false;
}
}
// If queen can not be place in any row
// in this column col then return false
return false;
}
/*
* This function solves the N Queen problem using Branch
* and Bound. It mainly uses solveNQueensUtil() to solve
* the problem. It returns false if queens cannot be
* placed, otherwise return true and prints placement of
* queens in the form of 1s. Please note that there may
* be more than one solutions, this function prints one
* of the feasible solutions.
*/
static boolean solveNQueens()
{
int board[][] = new int[N][N];
// Helper matrices
int slashCode[][] = new int[N][N];
int backslashCode[][] = new int[N][N];
// Arrays to tell us which rows are occupied
boolean[] rowLookup = new boolean[N];
// Keep two arrays to tell us
// which diagonals are occupied
boolean slashCodeLookup[] = new boolean[2 * N - 1];
boolean backslashCodeLookup[] = new boolean[2 * N - 1];
// Initialize helper matrices
for(int r = 0; r < N; r++)
for(int c = 0; c < N; c++)
{
slashCode[r] = r + c;
backslashCode[r] = r - c + 7;
}
if (solveNQueensUtil(board, 0, slashCode,
backslashCode, rowLookup,
slashCodeLookup,
backslashCodeLookup) == false)
{
System.out.printf("Solution does not exist");
return false;
}
// Solution found
printSolution(board);
return true;
}
// Driver code
public static void main(String[] args)
{
solveNQueens();
}
}
// This code is contributed by sujitmeshram
Python3
""" Python3 program to solve N Queen Problem
using Branch or Bound """
N = 8
""" A utility function to print solution """
def printSolution(board):
for i in range(N):
for j in range(N):
print(board[i][j], end = " ")
print()
""" A Optimized function to check if
a queen can be placed on board[row][col] """
def isSafe(row, col, slashCode, backslashCode,
rowLookup, slashCodeLookup,
backslashCodeLookup):
if (slashCodeLookup[slashCode[row][col]] or
backslashCodeLookup[backslashCode[row][col]] or
rowLookup[row]):
return False
return True
""" A recursive utility function
to solve N Queen problem """
def solveNQueensUtil(board, col, slashCode, backslashCode,
rowLookup, slashCodeLookup,
backslashCodeLookup):
""" base case: If all queens are
placed then return True """
if(col >= N):
return True
for i in range(N):
if(isSafe(i, col, slashCode, backslashCode,
rowLookup, slashCodeLookup,
backslashCodeLookup)):
""" Place this queen in board[i][col] """
board[i][col] = 1
rowLookup[i] = True
slashCodeLookup[slashCode[i][col]] = True
backslashCodeLookup[backslashCode[i][col]] = True
""" recur to place rest of the queens """
if(solveNQueensUtil(board, col + 1,
slashCode, backslashCode,
rowLookup, slashCodeLookup,
backslashCodeLookup)):
return True
""" If placing queen in board[i][col]
doesn't lead to a solution,then backtrack """
""" Remove queen from board[i][col] """
board[i][col] = 0
rowLookup[i] = False
slashCodeLookup[slashCode[i][col]] = False
backslashCodeLookup[backslashCode[i][col]] = False
""" If queen can not be place in any row in
this column col then return False """
return False
""" This function solves the N Queen problem using
Branch or Bound. It mainly uses solveNQueensUtil()to
solve the problem. It returns False if queens
cannot be placed,otherwise return True or
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions,this function prints one of the
feasible solutions."""
def solveNQueens():
board = [[0 for i in range(N)]
for j in range(N)]
# helper matrices
slashCode = [[0 for i in range(N)]
for j in range(N)]
backslashCode = [[0 for i in range(N)]
for j in range(N)]
# arrays to tell us which rows are occupied
rowLookup = [False] * N
# keep two arrays to tell us
# which diagonals are occupied
x = 2 * N - 1
slashCodeLookup = [False] * x
backslashCodeLookup = [False] * x
# initialize helper matrices
for rr in range(N):
for cc in range(N):
slashCode[rr][cc] = rr + cc
backslashCode[rr][cc] = rr - cc + 7
if(solveNQueensUtil(board, 0, slashCode, backslashCode,
rowLookup, slashCodeLookup,
backslashCodeLookup) == False):
print("Solution does not exist")
return False
# solution found
printSolution(board)
return True
# Driver Cde
solveNQueens()
# This code is contributed by SHUBHAMSINGH10
Javascript
<script>
// JavaScript program to solve N Queen Problem
// using Branch and Bound
let N = 8;
// A utility function to print solution
function printSolution(board)
{
let N = board.length;
for(let i = 0; i < N; i++)
{
for(let j = 0; j < N; j++)
document.write(board[i][j]+" ");
document.write("<br>");
}
}
// A Optimized function to check if a queen
// can be placed on board[row][col]
function isSafe(row,col,slashCode,backslashCode,rowLookup,slashCodeLookup,backslashCodeLookup)
{
if (slashCodeLookup[slashCode[row][col]] ||
backslashCodeLookup[backslashCode[row][col]] ||
rowLookup[row])
return false;
return true;
}
// A recursive utility function to
// solve N Queen problem
function solveNQueensUtil(board,col,slashCode,
backslashCode,rowLookup,slashCodeLookup,backslashCodeLookup)
{
// Base case: If all queens are placed
// then return true
//let N = board.length;
if (col >= N)
return true;
// Consider this column and try placing
// this queen in all rows one by one
for(let i = 0; i < N; i++)
{
// Check if queen can be placed on board[i][col]
if (isSafe(i, col, slashCode, backslashCode,
rowLookup, slashCodeLookup,
backslashCodeLookup))
{
// Place this queen in board[i][col]
board[i][col] = 1;
rowLookup[i] = true;
slashCodeLookup[slashCode[i][col]] = true;
backslashCodeLookup[backslashCode[i][col]] = true;
// recur to place rest of the queens
if (solveNQueensUtil(
board, col + 1, slashCode,
backslashCode, rowLookup,
slashCodeLookup,
backslashCodeLookup))
return true;
// If placing queen in board[i][col] doesn't
// lead to a solution, then backtrack
// Remove queen from board[i][col]
board[i][col] = 0;
rowLookup[i] = false;
slashCodeLookup[slashCode[i][col]] = false;
backslashCodeLookup[backslashCode[i][col]] = false;
}
}
// If queen can not be place in any row
// in this column col then return false
return false;
}
/*
* This function solves the N Queen problem using Branch
* and Bound. It mainly uses solveNQueensUtil() to solve
* the problem. It returns false if queens cannot be
* placed, otherwise return true and prints placement of
* queens in the form of 1s. Please note that there may
* be more than one solutions, this function prints one
* of the feasible solutions.
*/
function solveNQueens()
{
let board = new Array(N);
// Helper matrices
let slashCode = new Array(N);
let backslashCode = new Array(N);
for(let i=0;i<N;i++)
{
board[i]=new Array(N);
slashCode[i]=new Array(N);
backslashCode[i]=new Array(N);
for(let j=0;j<N;j++)
{
board[i][j]=0;
slashCode[i][j]=0;
backslashCode[i][j]=0;
}
}
// Arrays to tell us which rows are occupied
let rowLookup = new Array(N);
for(let i=0;i<N;i++)
rowLookup[i]=false;
// Keep two arrays to tell us
// which diagonals are occupied
let slashCodeLookup = new Array(2 * N - 1);
let backslashCodeLookup = new Array(2 * N - 1);
for(let i=0;i<2*N-1;i++)
{
slashCodeLookup[i]=false;
backslashCodeLookup[i]=false;
}
// Initialize helper matrices
for(let r = 0; r < N; r++)
for(let c = 0; c < N; c++)
{
slashCode[r] = r + c;
backslashCode[r] = r - c + 7;
}
if (solveNQueensUtil(board, 0, slashCode,
backslashCode, rowLookup,
slashCodeLookup,
backslashCodeLookup) == false)
{
document.write("Solution does not exist");
return false;
}
// Solution found
printSolution(board);
return true;
}
// Driver code
solveNQueens();
// This code is contributed by avanitrachhadiya2155
</script>
Aporte:
Ingrese el número de filas para el tablero cuadrado: 8
Producción :
1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0
Referencias:
https://en.wikipedia.org/wiki/Eight_queens_puzzle
www.cs.cornell.edu/~wdtseng/icpc/notes/bt2.pdf Aditya Goel
contribuye con este artículo . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA