Problema de rata y botella envenenada

Dado N número de botellas en las que una botella está envenenada. Entonces, la tarea es averiguar el número mínimo de ratas necesarias para identificar la botella envenenada. Una rata puede beber cualquier cantidad de botellas a la vez. 

Ejemplos: 

Input: N = 4 
Output: 2

Input: N = 100
Output: 7

Enfoque: 
Partamos del caso base. 

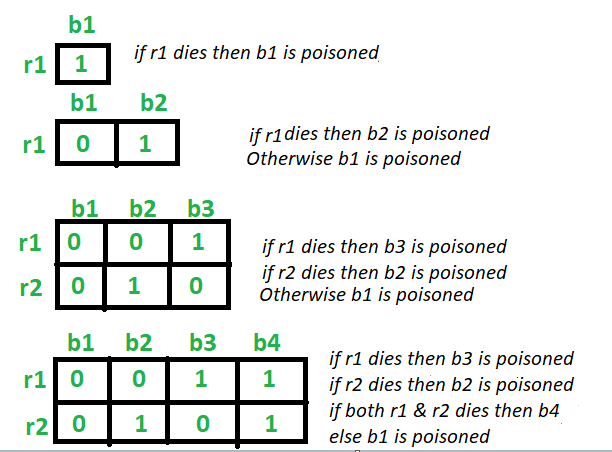
• Para 2 botellas: Tomar una rata (R1) . Si la rata R1 bebe la botella 1 y muere, entonces la botella 1 es venenosa. De lo contrario, la botella 2 es venenosa. Por lo tanto, 1 rata es suficiente para identificar
• Para 3 botellas: Tomar dos ratas (R1) y (R2) . Si la rata R1 bebe la botella 1 y la botella 3 y muere, entonces la botella 1 o la botella 3 son venenosas. Entonces la rata R2 bebe la botella 1 entonces. Si muere, entonces la botella 1 es venenosa, de lo contrario, la botella 3 es venenosa. 
  Ahora bien, si la rata R1 no muere después de beber de la botella 1 y la botella 3, entonces la botella 2 es venenosa. 
  Por lo tanto, 2 ratas son suficientes para identificar. 
   
• Para 4 botellas: Tomar dos ratas (R1) y (R2) . Si la rata R1 bebe la botella 1 y la botella 3 y muere, entonces la botella 1 o la botella 3 son venenosas. Entonces la rata R2 bebe la botella 1 entonces. Si muere, entonces la botella 1 es venenosa, de lo contrario, la botella 3 es venenosa. 
  Ahora bien, si la rata R1 no muere después de beber de la botella 1 y la botella 3, entonces la botella 2 o la botella 4 son venenosas. Entonces la rata R1 bebe la botella 2 entonces. Si muere, entonces la botella 2 es venenosa, de lo contrario, la botella 4 es venenosa. 
  Por lo tanto, 2 ratas son suficientes para identificar. 
   
• Para N botellas: 

El número mínimo de ratas necesarias es = ceil(log ₂ N))
 

A continuación se muestra la implementación del enfoque anterior:  

// C++ program to implement
// the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the minimum number of rats
int minRats(int n)
{
    return ceil(log2(n));
}
 
// Driver Code
int main()
{
    // Number of bottles
    int n = 1025;
 
    cout << "Minimum " << minRats(n)
         << " rat(s) are required"
         << endl;
 
    return 0;
}

// Java program to implement
// the above approach
class GFG
{
    public static double log2(int x)
    {
        return (Math.log(x) / Math.log(2));
    }
 
    // Function to find the minimum number of rats
    static int minRats(int n)
    {
        return (int)(Math.floor(log2(n)) + 1);
    }
     
    // Driver Code
    public static void main (String[] args)
    {
        // Number of bottles
        int n = 1025;
     
        System.out.println("Minimum " + minRats(n) +
                           " rat(s) are required");
    }   
}
 
// This code is contributed by AnkitRai01

# Python3 program to implement
# the above approach
import math
 
# Function to find the
# minimum number of rats
def minRats(n):
     
    return math.ceil(math.log2(n));
 
# Driver Code
 
# Number of bottles
n = 1025;
print("Minimum ", end = "")
print(minRats(n), end = " ")
print("rat(s) are required")
 
# This code is contributed
# by divyamohan123

// C# program to implement
// the above approach
using System;
 
class GFG
{
    public static double log2(int x)
    {
        return (Math.Log(x) / Math.Log(2));
    }
 
    // Function to find the minimum number of rats
    static int minRats(int n)
    {
        return (int)(Math.Floor(log2(n)) + 1);
    }
     
    // Driver Code
    public static void Main (String[] args)
    {
        // Number of bottles
        int n = 1025;
     
        Console.WriteLine("Minimum " + minRats(n) +
                          " rat(s) are required");
    }
}
 
// This code is contributed by 29AjayKumar

<script>
 
// Javascript program to implement
// the above approach
 
// Function to find the minimum number of rats
function minRats(n)
{
    return Math.ceil(Math.log2(n));
}
 
// Driver Code
 
// Number of bottles
var n = 1025;
document.write("Minimum " + minRats(n) +
               " rat(s) are required");
                
// This code is contributed by importantly
 
</script>

Minimum 11 rat(s) are required