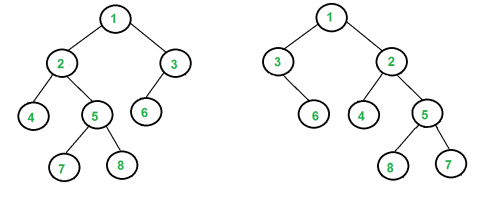
Escribe una función para detectar si dos árboles son isomorfos. Dos árboles se denominan isomorfos si uno de ellos se puede obtener del otro mediante una serie de cambios, es decir, intercambiando los hijos izquierdo y derecho de varios Nodes. Cualquier número de Nodes en cualquier nivel puede intercambiar sus hijos. Dos árboles vacíos son isomorfos.
Por ejemplo, los siguientes dos árboles son isomorfos con los siguientes subárboles invertidos: 2 y 3, NULL y 6, 7 y 8.
C++
// A C++ program to check if two given trees are isomorphic
#include <iostream>
using namespace std;
/* A binary tree node has data, pointer to left and right children */
struct node
{
int data;
struct node* left;
struct node* right;
};
/* Given a binary tree, print its nodes in reverse level order */
bool isIsomorphic(node* n1, node *n2)
{
// Both roots are NULL, trees isomorphic by definition
if (n1 == NULL && n2 == NULL)
return true;
// Exactly one of the n1 and n2 is NULL, trees not isomorphic
if (n1 == NULL || n2 == NULL)
return false;
if (n1->data != n2->data)
return false;
// There are two possible cases for n1 and n2 to be isomorphic
// Case 1: The subtrees rooted at these nodes have NOT been "Flipped".
// Both of these subtrees have to be isomorphic, hence the &&
// Case 2: The subtrees rooted at these nodes have been "Flipped"
return
(isIsomorphic(n1->left,n2->left) && isIsomorphic(n1->right,n2->right))||
(isIsomorphic(n1->left,n2->right) && isIsomorphic(n1->right,n2->left));
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newNode(int data)
{
node* temp = new node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return (temp);
}
/* Driver program to test above functions*/
int main()
{
// Let us create trees shown in above diagram
struct node *n1 = newNode(1);
n1->left = newNode(2);
n1->right = newNode(3);
n1->left->left = newNode(4);
n1->left->right = newNode(5);
n1->right->left = newNode(6);
n1->left->right->left = newNode(7);
n1->left->right->right = newNode(8);
struct node *n2 = newNode(1);
n2->left = newNode(3);
n2->right = newNode(2);
n2->right->left = newNode(4);
n2->right->right = newNode(5);
n2->left->right = newNode(6);
n2->right->right->left = newNode(8);
n2->right->right->right = newNode(7);
if (isIsomorphic(n1, n2) == true)
cout << "Yes";
else
cout << "No";
return 0;
}
Java
// An iterative java program to solve tree isomorphism problem
/* A binary tree node has data, pointer to left and right children */
class Node
{
int data;
Node left, right;
Node(int item)
{
data = item;
left = right;
}
}
class BinaryTree
{
Node root1, root2;
/* Given a binary tree, print its nodes in reverse level order */
boolean isIsomorphic(Node n1, Node n2)
{
// Both roots are NULL, trees isomorphic by definition
if (n1 == null && n2 == null)
return true;
// Exactly one of the n1 and n2 is NULL, trees not isomorphic
if (n1 == null || n2 == null)
return false;
if (n1.data != n2.data)
return false;
// There are two possible cases for n1 and n2 to be isomorphic
// Case 1: The subtrees rooted at these nodes have NOT been
// "Flipped".
// Both of these subtrees have to be isomorphic.
// Case 2: The subtrees rooted at these nodes have been "Flipped"
return (isIsomorphic(n1.left, n2.left) &&
isIsomorphic(n1.right, n2.right))
|| (isIsomorphic(n1.left, n2.right) &&
isIsomorphic(n1.right, n2.left));
}
// Driver program to test above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
// Let us create trees shown in above diagram
tree.root1 = new Node(1);
tree.root1.left = new Node(2);
tree.root1.right = new Node(3);
tree.root1.left.left = new Node(4);
tree.root1.left.right = new Node(5);
tree.root1.right.left = new Node(6);
tree.root1.left.right.left = new Node(7);
tree.root1.left.right.right = new Node(8);
tree.root2 = new Node(1);
tree.root2.left = new Node(3);
tree.root2.right = new Node(2);
tree.root2.right.left = new Node(4);
tree.root2.right.right = new Node(5);
tree.root2.left.right = new Node(6);
tree.root2.right.right.left = new Node(8);
tree.root2.right.right.right = new Node(7);
if (tree.isIsomorphic(tree.root1, tree.root2) == true)
System.out.println("Yes");
else
System.out.println("No");
}
}
// This code has been contributed by Mayank Jaiswal
Python3
# Python program to check if two given trees are isomorphic
# A Binary tree node
class Node:
# Constructor to create the node of binary tree
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Check if the binary tree is isomorphic or not
def isIsomorphic(n1, n2):
# Both roots are None, trees isomorphic by definition
if n1 is None and n2 is None:
return True
# Exactly one of the n1 and n2 is None, trees are not
# isomorphic
if n1 is None or n2 is None:
return False
if n1.data != n2.data :
return False
# There are two possible cases for n1 and n2 to be isomorphic
# Case 1: The subtrees rooted at these nodes have NOT
# been "Flipped".
# Both of these subtrees have to be isomorphic, hence the &&
# Case 2: The subtrees rooted at these nodes have
# been "Flipped"
return ((isIsomorphic(n1.left, n2.left)and
isIsomorphic(n1.right, n2.right)) or
(isIsomorphic(n1.left, n2.right) and
isIsomorphic(n1.right, n2.left))
)
# Driver program to test above function
n1 = Node(1)
n1.left = Node(2)
n1.right = Node(3)
n1.left.left = Node(4)
n1.left.right = Node(5)
n1.right.left = Node(6)
n1.left.right.left = Node(7)
n1.left.right.right = Node(8)
n2 = Node(1)
n2.left = Node(3)
n2.right = Node(2)
n2.right.left = Node(4)
n2.right.right = Node(5)
n2.left.right = Node(6)
n2.right.right.left = Node(8)
n2.right.right.right = Node(7)
print ("Yes" if (isIsomorphic(n1, n2) == True) else "No")
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
using System;
// An iterative C# program to solve tree isomorphism problem
/* A binary tree node has data, pointer to left and right children */
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right;
}
}
public class BinaryTree
{
public Node root1, root2;
/* Given a binary tree, print its nodes in reverse level order */
public virtual bool isIsomorphic(Node n1, Node n2)
{
// Both roots are NULL, trees isomorphic by definition
if (n1 == null && n2 == null)
{
return true;
}
// Exactly one of the n1 and n2 is NULL, trees not isomorphic
if (n1 == null || n2 == null)
{
return false;
}
if (n1.data != n2.data)
{
return false;
}
// There are two possible cases for n1 and n2 to be isomorphic
// Case 1: The subtrees rooted at these nodes have NOT been
// "Flipped".
// Both of these subtrees have to be isomorphic.
// Case 2: The subtrees rooted at these nodes have been "Flipped"
return (isIsomorphic(n1.left, n2.left)
&& isIsomorphic(n1.right, n2.right))
|| (isIsomorphic(n1.left, n2.right)
&& isIsomorphic(n1.right, n2.left));
}
// Driver program to test above functions
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
// Let us create trees shown in above diagram
tree.root1 = new Node(1);
tree.root1.left = new Node(2);
tree.root1.right = new Node(3);
tree.root1.left.left = new Node(4);
tree.root1.left.right = new Node(5);
tree.root1.right.left = new Node(6);
tree.root1.left.right.left = new Node(7);
tree.root1.left.right.right = new Node(8);
tree.root2 = new Node(1);
tree.root2.left = new Node(3);
tree.root2.right = new Node(2);
tree.root2.right.left = new Node(4);
tree.root2.right.right = new Node(5);
tree.root2.left.right = new Node(6);
tree.root2.right.right.left = new Node(8);
tree.root2.right.right.right = new Node(7);
if (tree.isIsomorphic(tree.root1, tree.root2) == true)
{
Console.WriteLine("Yes");
}
else
{
Console.WriteLine("No");
}
}
}
// This code is contributed by Shrikant13
Javascript
<script>
// An iterative JavaScript program
// to solve tree isomorphism problem
/* A binary tree node has data, pointer to
left and right children */
class Node {
constructor(item) {
this.data = item;
this.left = null;
this.right = null;
}
}
class BinaryTree {
constructor() {
this.root1 = null;
this.root2 = null;
}
/* Given a binary tree, print its
nodes in reverse level order */
isIsomorphic(n1, n2) {
// Both roots are NULL, trees isomorphic by definition
if (n1 == null && n2 == null) {
return true;
}
// Exactly one of the n1 and n2 is NULL,
// trees not isomorphic
if (n1 == null || n2 == null) {
return false;
}
if (n1.data != n2.data) {
return false;
}
// There are two possible cases for
// n1 and n2 to be isomorphic
// Case 1: The subtrees rooted at
// these nodes have NOT been
// "Flipped".
// Both of these subtrees have to be isomorphic.
// Case 2: The subtrees rooted at these nodes
// have been "Flipped"
return (
(this.isIsomorphic(n1.left, n2.left) &&
this.isIsomorphic(n1.right, n2.right)) ||
(this.isIsomorphic(n1.left, n2.right) &&
this.isIsomorphic(n1.right, n2.left))
);
}
}
// Driver program to test above functions
var tree = new BinaryTree();
// Let us create trees shown in above diagram
tree.root1 = new Node(1);
tree.root1.left = new Node(2);
tree.root1.right = new Node(3);
tree.root1.left.left = new Node(4);
tree.root1.left.right = new Node(5);
tree.root1.right.left = new Node(6);
tree.root1.left.right.left = new Node(7);
tree.root1.left.right.right = new Node(8);
tree.root2 = new Node(1);
tree.root2.left = new Node(3);
tree.root2.right = new Node(2);
tree.root2.right.left = new Node(4);
tree.root2.right.right = new Node(5);
tree.root2.left.right = new Node(6);
tree.root2.right.right.left = new Node(8);
tree.root2.right.right.right = new Node(7);
if (tree.isIsomorphic(tree.root1, tree.root2) == true) {
document.write("Yes");
} else {
document.write("No");
}
</script>
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA