Dado el teclado numérico del móvil. Solo puede presionar los botones que están hacia arriba, hacia la izquierda, hacia la derecha o hacia abajo hasta el botón actual o puede elegir presionar el mismo botón nuevamente. Los botones de esquina redondeada (es decir, * y #) son movimientos inválidos.
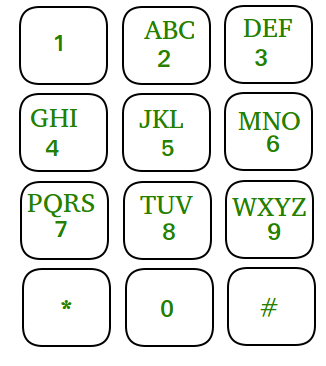
Dado un número N , debe encontrar los distintos números de longitud N que puede marcar comenzando desde cualquier número del 0 al 9, con la restricción de que solo puede moverse hacia arriba, hacia la izquierda, hacia la derecha o hacia abajo desde el último número que presionó, o puede elegir presionar el mismo botón nuevamente.
Ejemplos:
Entrada: N = 1
Salida: 10
0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 son los números posibles.Entrada: N = 2
Salida: 36
Todos los números posibles son 00, 08, 11, 12, 14, 21, 22, 23, 25, …Entrada: N = 6
Salida: 7990
Enfoque: Hemos visto muchas soluciones para resolver este problema aquí .
Sea X n i el conteo de números de n dígitos que terminan en i .
Entonces, por esta notación,
X 1 0 = 1 que es {0}
X 1 1 = 1 que es {1}
X 1 2 = 1 que es {2}
X 1 3 = 1 que es {3}
y
X 2 0 = 2 que son {00 , 80}
X 2 1 = 3 que son {11, 21, 41}
X 2 2 = 4 que son {22, 12, 32, 52}
La idea central es, si conoces X n i , qué información puedes obtener sobre X n + 1 j
Veamos con la ayuda de un ejemplo:
Supongamos que sabemos, X 2 1 = 3 que son {11, 21, 41}
Debido a que el último dígito de todos estos números es 1 , veamos los posibles movimientos que podemos tener desde 1 :
- Presionando 1 nuevamente.
- Presionando 2 (moviéndose a la derecha).
- Presionando 4 (moviéndose hacia abajo)
Ahora podemos elegir cualquier elemento de nuestro conjunto {11, 21, 41} y realizar cualquier movimiento válido:
- {111, 211, 411} se puede lograr con el primer movimiento.
- {112, 212, 412} con el segundo movimiento.
- Y {114, 214, 414} con el tercero.
Podemos ver que haciendo cualquier movimiento posible, obtenemos el conjunto del mismo tamaño con cada movimiento. es decir, había 3 elementos en el conjunto de números de dos dígitos que terminan en 1, obtuvimos un conjunto del mismo tamaño (3) con cada movimiento posible desde 1.
Entonces, se puede ver que X 2 1 contribuye en números de 3 dígitos de la siguiente manera:
X 3 1 += X 2 1 X 3 2 + = X 2 1 X 3 4 + = X 2 1
Entonces, en general, si sabemos acerca de X n i , sabemos el recuento que contribuye a X n+1 j , donde j es cada movimiento posible desde i. ![]()
donde 0<=j<=9 y de j podemos tener un válido para i
La idea es enumerar primero todas las direcciones posibles de cada clave dada y mantener una array de 10 elementos donde el elemento en cada índice almacene el recuento de números que terminan con ese índice.
Por ejemplo, los valores iniciales de la array son:
Valor 1 1 1 1 1 1 1 1 1 1
Índice 0 1 2 3 4 5 6 7 8 9
Y el resultado inicial para n = 1 es la suma de todos los elementos de la array, es decir, 1+1+1+1+1+1+1+1+1+1 = 10, hay 10 números de 1 dígito que se pueden marcar.
¿Cómo actualizar la array para n > 1?
Primero enumeremos todas las direcciones para todos los números dados:
De A (Posibles movimientos) 0 0, 8 1 1, 2, 4 2 2, 1, 3, 5 3 3, 6, 2 4 4, 1, 7, 5 5 5, 4, 6, 2, 8 6 6, 3, 5, 9 7 7, 4, 8 8 8, 5, 0, 7, 9 9 9, 6, 8
La primera fila de la tabla anterior indica que, si el último dígito del número era cero, podemos movernos a 0 u 8.
Echemos un vistazo detallado al enfoque para N = 2
Para N = 1, Arr[10] es {1, 1, 1, 1, 1, 1, 1, 1, 1, 1} lo que indica que hay números Arr[i] que terminan con el índice i Vamos a crear una nueva array,
digamos Arr2[10] = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
Ahora, para 0, los movimientos posibles son 0 y 8.
Ya sabemos
que contribuiría 1 a {0, 8 } es decir,
Arr2[10] = {1, 0, 0, 0, 0, 0, 0, 0, 1, 0} Para 1, los movimientos posibles son
1, 2, 4
ya sabemos
que contribuiría 1 a {1, 2, 4} ie
Arr2[10] = {1, 1, 1, 0, 1, 0, 0, 0, 1, 0} Para
2, los movimientos posibles son 2, 1, 3, 4
que ya sabemos
Eso contribuiría 1 a {2, 1, 3, 4}
Arr2[10] = {1, 2, 2, 1, 1, 0, 0, 0, 1, 0}
y así sucesivamente….
Arr2[10] = {2, 3, 4, 3, 4, 5, 4, 3, 5, 3}
Suma = 2+3+4+3+4+5+4+3+5+3 = 36 (Para N=2)
Arr2 ahora contiene los valoresy puede considerarse como punto de partida para n=3 y el proceso continúa .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the approach
#include <iostream>
#include <list>
using namespace std;
#define MAX 10
// Function to return the count of numbers possible
int getCount(int n)
{
// Array of list storing possible direction
// for each number from 0 to 9
// mylist[i] stores possible moves from index i
list<int> mylist[MAX];
// Initializing list
mylist[0].assign({ 0, 8 });
mylist[1].assign({ 1, 2, 4 });
mylist[2].assign({ 2, 1, 3, 5 });
mylist[3].assign({ 3, 6, 2 });
mylist[4].assign({ 4, 1, 7, 5 });
mylist[5].assign({ 5, 4, 6, 2, 8 });
mylist[6].assign({ 6, 3, 5, 9 });
mylist[7].assign({ 7, 4, 8 });
mylist[8].assign({ 8, 5, 0, 7, 9 });
mylist[9].assign({ 9, 6, 8 });
// Storing values for n = 1
int Arr[MAX] = { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };
for (int i = 2; i <= n; i++) {
// To store the values for n = i
int Arr2[MAX] = { 0 };
// Loop to iterate through each index
for (int j = 0; j < MAX; j++) {
// For each move possible from j
// Increment the value of possible
// move positions by Arr[j]
for (int x : mylist[j]) {
Arr2[x] += Arr[j];
}
}
// Update Arr[] for next iteration
for (int j = 0; j < MAX; j++)
Arr[j] = Arr2[j];
}
// Find the count of numbers possible
int sum = 0;
for (int i = 0; i < MAX; i++)
sum += Arr[i];
return sum;
}
// Driver code
int main()
{
int n = 2;
cout << getCount(n);
return 0;
}
Java
// Java implementation of the approach
class GFG
{
static int MAX = 10;
// Function to return the count of numbers possible
static int getCount(int n)
{
// Array of list storing possible direction
// for each number from 0 to 9
// list[i] stores possible moves from index i
int [][] list = new int[MAX][];
// Initializing list
list[0] = new int [] { 0, 8 };
list[1] = new int [] { 1, 2, 4 };
list[2] = new int [] { 2, 1, 3, 5 };
list[3] = new int [] { 3, 6, 2 };
list[4] = new int [] { 4, 1, 7, 5 };
list[5] = new int [] { 5, 4, 6, 2, 8 };
list[6] = new int [] { 6, 3, 5, 9 };
list[7] = new int [] { 7, 4, 8 };
list[8] = new int [] { 8, 5, 0, 7, 9 };
list[9] = new int [] { 9, 6, 8 };
// Storing values for n = 1
int Arr[] = new int [] { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };
for (int i = 2; i <= n; i++)
{
// To store the values for n = i
int Arr2[] = new int [MAX];
// Loop to iterate through each index
for (int j = 0; j < MAX; j++)
{
// For each move possible from j
// Increment the value of possible
// move positions by Arr[j]
for (int x = 0; x < list[j].length; x++)
{
Arr2[list[j][x]] += Arr[j];
}
}
// Update Arr[] for next iteration
for (int j = 0; j < MAX; j++)
Arr[j] = Arr2[j];
}
// Find the count of numbers possible
int sum = 0;
for (int i = 0; i < MAX; i++)
sum += Arr[i];
return sum;
}
// Driver code
public static void main (String[] args)
{
int n = 2;
System.out.println(getCount(n));
}
}
// This code is contributed by ihritik
Python3
# Python3 implementation of the approach MAX = 10 # Function to return the count of numbers possible def getCount(n): global MAX # Array of list storing possible direction # for each number from 0 to 9 # mylist[i] stores possible moves from index i mylist = [[] for i in range(MAX)] # Initializing list mylist[0] = [ 0, 8 ] mylist[1] = [ 1, 2, 4 ] mylist[2] = [ 2, 1, 3, 5 ] mylist[3] = [ 3, 6, 2 ] mylist[4] = [ 4, 1, 7, 5 ] mylist[5] = [ 5, 4, 6, 2, 8 ] mylist[6] = [ 6, 3, 5, 9 ] mylist[7] = [ 7, 4, 8 ] mylist[8] = [ 8, 5, 0, 7, 9 ] mylist[9] = [ 9, 6, 8 ] # Storing values for n = 1 Arr = [1 for i in range(MAX)] for i in range(2,n+1): # To store the values for n = i Arr2 = [0 for i in range(MAX)] # Loop to iterate through each index for j in range(MAX): # For each move possible from j # Increment the value of possible # move positions by Arr[j] for x in mylist[j]: Arr2[x] += Arr[j] # Update Arr[] for next iteration for j in range(MAX): Arr[j] = Arr2[j] # Find the count of numbers possible sum = 0 for i in range(MAX): sum += Arr[i] return sum # Driver code n = 2 print(getCount(n)) # This code is contributed by shinjanpatra
C#
// C# implementation of the approach
using System;
class GFG
{
static int MAX = 10;
// Function to return the count of numbers possible
static int getCount(int n)
{
// Array of list storing possible direction
// for each number from 0 to 9
// list[i] stores possible moves from index i
int [][] list = new int[MAX][];
// Initializing list
list[0] = new int [] { 0, 8 };
list[1] = new int [] { 1, 2, 4 };
list[2] = new int [] { 2, 1, 3, 5 };
list[3] = new int [] { 3, 6, 2 };
list[4] = new int [] { 4, 1, 7, 5 };
list[5] = new int [] { 5, 4, 6, 2, 8 };
list[6] = new int [] { 6, 3, 5, 9 };
list[7] = new int [] { 7, 4, 8 };
list[8] = new int [] { 8, 5, 0, 7, 9 };
list[9] = new int [] { 9, 6, 8 };
// Storing values for n = 1
int [] Arr = new int [] { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };
for (int i = 2; i <= n; i++)
{
// To store the values for n = i
int [] Arr2 = new int [MAX];
// Loop to iterate through each index
for (int j = 0; j < MAX; j++)
{
// For each move possible from j
// Increment the value of possible
// move positions by Arr[j]
for (int x = 0; x < list[j].Length; x++)
{
Arr2[list[j][x]] += Arr[j];
}
}
// Update Arr[] for next iteration
for (int j = 0; j < MAX; j++)
Arr[j] = Arr2[j];
}
// Find the count of numbers possible
int sum = 0;
for (int i = 0; i < MAX; i++)
sum += Arr[i];
return sum;
}
// Driver code
public static void Main ()
{
int n = 2;
Console.WriteLine(getCount(n));
}
}
// This code is contributed by ihritik
Javascript
<script>
// JavaScript implementation of the approach
let MAX = 10
// Function to return the count of numbers possible
function getCount(n)
{
// Array of list storing possible direction
// for each number from 0 to 9
// mylist[i] stores possible moves from index i
let mylist = new Array(MAX).fill(new Array());
// Initializing list
mylist[0] = [ 0, 8 ];
mylist[1] = [ 1, 2, 4 ];
mylist[2] = [ 2, 1, 3, 5 ];
mylist[3] = [ 3, 6, 2 ];
mylist[4] = [ 4, 1, 7, 5 ];
mylist[5] = [ 5, 4, 6, 2, 8 ];
mylist[6] = [ 6, 3, 5, 9 ];
mylist[7] = [ 7, 4, 8 ];
mylist[8] = [ 8, 5, 0, 7, 9 ];
mylist[9] = [ 9, 6, 8 ];
// Storing values for n = 1
let Arr = new Array(MAX).fill(1);
for (let i = 2; i <= n; i++) {
// To store the values for n = i
let Arr2 = new Array(MAX).fill(0);
// Loop to iterate through each index
for (let j = 0; j < MAX; j++) {
// For each move possible from j
// Increment the value of possible
// move positions by Arr[j]
for (let x in mylist[j]) {
Arr2[x] += Arr[j];
}
}
// Update Arr[] for next iteration
for (let j = 0; j < MAX; j++)
Arr[j] = Arr2[j];
}
// Find the count of numbers possible
let sum = 0;
for (let i = 0; i < MAX; i++)
sum += Arr[i];
return sum;
}
// Driver code
let n = 2;
document.write(getCount(n),"</br>");
// This code is contributed by shinjanpatra
</script>
36
Complejidad de tiempo: O(N)
Complejidad de espacio: O(1)
Publicación traducida automáticamente
Artículo escrito por Ankur Goel y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA