Problema del vendedor ambulante | Conjunto 2 (Aproximado usando MST)

Presentamos el problema del vendedor ambulante y discutimos las soluciones de programación ingenua y dinámica para el problema en la publicación anterior . Ambas soluciones son inviables. De hecho, no existe una solución de tiempo polinomial disponible para este problema, ya que se trata de un problema NP-Hard conocido. Sin embargo, existen algoritmos aproximados para resolver el problema. Los algoritmos aproximados funcionan solo si la instancia del problema satisface Triangle-Inequality. 

Triángulo-Desigualdad: El camino menos distante para llegar a un vértice j desde i siempre es llegar a j directamente desde i, en lugar de a través de algún otro vértice k (o vértices), es decir, dis(i, j) siempre es menor o igual a dis(i, k) + dist(k, j). El Triángulo-Desigualdad se cumple en muchas situaciones prácticas. 

Cuando la función de costo satisface la desigualdad del triángulo, podemos diseñar un algoritmo aproximado para TSP que devuelva un recorrido cuyo costo nunca sea más del doble del costo de un recorrido óptimo. La idea es utilizar M inimum S panning Tree (MST). A continuación se muestra el algoritmo basado en MST. 

Algoritmo: 

1. Sea 1 el punto inicial y final de vendedor. 
2. Construya MST a partir de 1 como root utilizando el Algoritmo de Prim .
3. Enumere los vértices visitados en la caminata de preorden del MST construido y agregue 1 al final. 

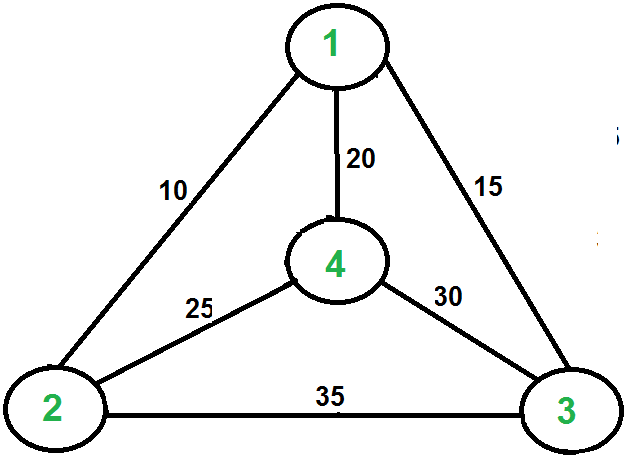
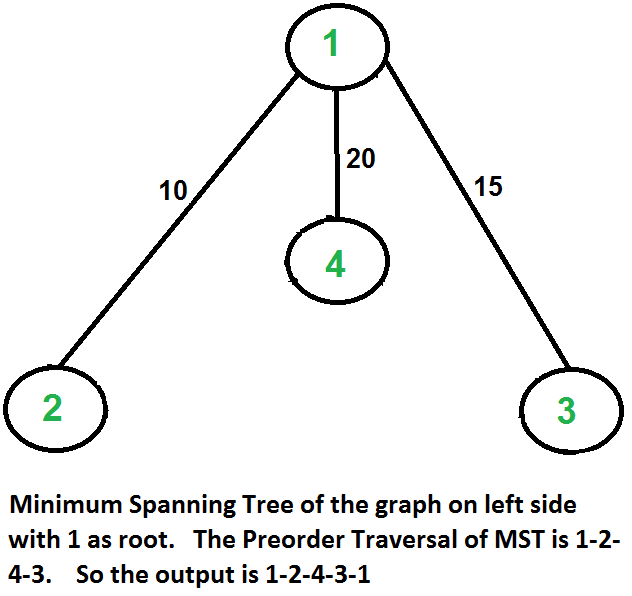
Consideremos el siguiente ejemplo. El primer diagrama es el gráfico dado. El segundo diagrama muestra MST construido con 1 como raíz. El recorrido previo al pedido de MST es 1-2-4-3. Agregar 1 al final da 1-2-4-3-1, que es el resultado de este algoritmo.

 

 

  

En este caso, el algoritmo aproximado produce el recorrido óptimo, pero es posible que no produzca el recorrido óptimo en todos los casos. 

¿Cómo es este algoritmo 2-aproximado? 

El costo de la salida producida por el algoritmo anterior nunca es más del doble del costo de la mejor salida posible. Veamos cómo se garantiza esto con el algoritmo anterior. 

Definamos un término paseo completo para entender esto. Una caminata completa enumera todos los vértices cuando se visitan por primera vez en orden previo, también enumera los vértices cuando se devuelven después de que se visita un subárbol en orden previo. La caminata completa del árbol anterior sería 1-2-1-4-1-3-1. 

Los siguientes son algunos hechos importantes que prueban la 2-aproximación. 

1. El costo de la mejor gira posible de Travelling Salesman nunca es menor que el costo de MST. (La definición de MST dice que es un árbol de costo mínimo que conecta todos los vértices). 
2. El costo total de la caminata completa es como máximo el doble del costo de MST (cada borde de MST se visita como máximo dos veces) 
3. El resultado del algoritmo anterior es menor que el costo de una caminata completa. En el algoritmo anterior, imprimimos la caminata de pedido anticipado como salida. En el recorrido de preorden, dos o más bordes del recorrido completo se reemplazan con un solo borde. Por ejemplo, 2-1 y 1-4 se reemplazan por 1 arista 2-4. Entonces, si el gráfico sigue la desigualdad triangular, entonces esto siempre es cierto. 

De las tres afirmaciones anteriores, podemos concluir que el costo de salida producido por el algoritmo aproximado nunca es más del doble del costo de la mejor solución posible. 

Hemos discutido un algoritmo aproximado de 2 muy simple para el problema del viajante de comercio. Hay otros mejores algoritmos aproximados para el problema. Por ejemplo , el algoritmo de Christofides es un algoritmo aproximado de 1,5. Pronto discutiremos estos algoritmos en publicaciones separadas.