Cada ocurrencia física en el universo de la física incluye algún tipo de atracción o repulsión, lo que hace que el universo exista de una manera única. El medio ambiente permanece en un estado bien equipado y equilibrado debido a la atracción y repulsión entre partículas. Cuando estas atracciones y repulsiones se manipulan para perturbar o variar, los resultados de las observaciones pueden ser notables.
Considere los electrones de un átomo: si se interrumpe la atracción entre los protones en el núcleo y los electrones en las capas, el átomo puede destruirse. Durante mucho tiempo, los físicos han estado fascinados por el lado cuantitativo de la física, ya que ayuda en la comprensión de conceptos y el desarrollo de nuevas teorías e ideas.
En 1785, un físico francés llamado Charles Augustin de Coulomb acuñó una relación matemática medible entre dos cuerpos cargados eléctricamente. La ley de Coulomb, a menudo conocida como la ley del cuadrado inverso de Coulomb , es una ecuación que ayuda a determinar el grado de repulsión o fuerza de atracción entre dos partículas cargadas.
Ley de Coulomb
La Ley de Coulomb describe la fuerza que existe entre dos cargas puntuales. El término carga puntual se refiere al hecho de que el tamaño de los objetos cargados linealmente es relativamente pequeño en comparación con la distancia entre ellos en la física. Como resultado, las tratamos como cargas puntuales ya que calcular la fuerza de atracción/repulsión entre ellas es simple.
Por lo tanto, la Ley de Coulomb se puede expresar como:
La fuerza de atracción o repulsión entre dos cuerpos cargados es directamente proporcional al producto de sus cargas e inversamente proporcional al cuadrado de la distancia que los separa, según la ley de Coulomb . Actúa sobre la línea que une las dos cargas que se denominan cargas puntuales .
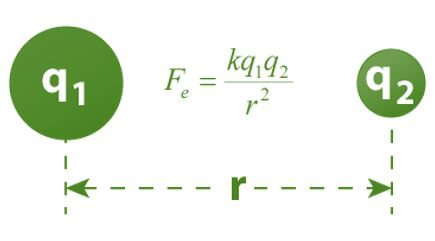
Representación pictórica de la ley de Coulomb
En general, el enunciado tiene dos cargas, q 1yq 2 . La fuerza de atracción/repulsión entre las cargas es ‘F’, y la distancia entre ellas es ‘r’. Entonces matemáticamente la ley de Coulomb se da como:
- La fuerza electrostática, F, es directamente proporcional al producto de la magnitud de las cargas en contacto, es decir, F ∝ q 1 q 2
- La fuerza electrostática, F, es inversamente proporcional al cuadrado de la distancia entre las dos cargas en contacto, es decir, F ∝ 1/r 2
Combinemos lo anterior con la relación como
F ∝ q 1 q 2 / r 2
Ahora, introduzca una nueva constante de proporcionalidad k como,
F = kq 1 q 2 / r 2
donde k es la constante de proporcionalidad y es igual a 1/4πε0, aquí ε0 se llama epsilon not, que indica la permitividad de un vacío. El valor calculado de k es 9 × 10 9 Nm 2 /C 2 .
Las cargas iguales se repelen, mientras que las cargas diferentes se atraen, según Coulomb. Esto significa que las cargas del mismo signo se repelen, mientras que las cargas de signos opuestos se atraen.
Ley de Coulomb en forma vectorial
Hay dos tipos de cantidades físicas: Escalares (con una sola magnitud) y Vectores (con muchas magnitudes) (aquellas cantidades con magnitud y dirección). Debido a que tiene tanto magnitud como dirección, la fuerza es una cantidad vectorial. En forma de vectores, la ley de Coulomb se puede reescribir. Recuerde que el vector «F» se denota como ![]() , y el vector «r» se denota como
, y el vector «r» se denota como ![]() , y así sucesivamente.
, y así sucesivamente.
Digamos que hay dos cargas, q 1 y q 2 , con r 1 y r 2 como vectores de ubicación. Como ambas cargas son del mismo signo, existirá una fuerza de repulsión entre ellas. Sea F 12 la fuerza sobre la carga q 1 debida a q 2 , y sea F 21 la fuerza sobre la carga q 2 debida a la carga q 1 . El vector r 21 es el vector coincidente de q 1 a q 2 .
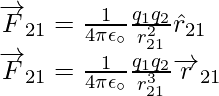
Cuando utilice la Ley de Coulomb para calcular la fuerza entre dos cargas puntuales, tenga en cuenta los siguientes puntos. Debido a que ambas cargas son inherentemente opuestas, la forma vectorial de la ecuación no se ve afectada por sus signos.
Debido al cambio en el vector de posición, la fuerza repulsiva F 21 , que es la fuerza sobre la carga q 1 debida a q 2 , y otra fuerza repulsiva F 21 , que es la fuerza sobre la carga q 2 debida a q 1 , tienen signos opuestos .
F 12 = – F 21
Esto se debe al hecho de que el vector de posición de la fuerza F 12 es r 12 , mientras que el vector de posición de la fuerza F 21 es r 21 .
r 21 = r 2 – r 1
y
r 12 = r 1 – r 2
Debido a que los signos de r 21 y r 12 son opuestos, producen fuerzas con signos opuestos. Esto demuestra que la Ley de Coulomb es compatible con la Tercera Ley de Newton, que establece que toda acción tiene una reacción igual y opuesta. Cuando dos cargas están presentes en el vacío, la Ley de Coulomb determina la fuerza entre ellas. Esto se debe al hecho de que en el vacío, las cargas no se ven afectadas por otra materia o partículas.
Limitaciones de la Ley de Coulomb
La Ley de Coulomb se basa en un conjunto de suposiciones y no puede emplearse de la misma manera que otras fórmulas universales. Los siguientes puntos están cubiertos por la ley:
- Si las cargas son estáticas, podemos utilizar la fórmula (en posición de reposo)
- Cuando se trata de cargas que tienen una forma normal y uniforme, la fórmula es sencilla de emplear; pero, cuando se trata de cargas que tienen formas irregulares, se vuelve demasiado complicado.
- Solo cuando las moléculas de solvente entre las partículas son significativamente más grandes que ambas cargas, la fórmula es válida.
Problemas basados en la ley de Coulomb
Problema 1: ¿Cuál será la fuerza electrostática entre las dos cargas puntuales de cargas +2μC y +4μC se repelen con una fuerza de 20N cuando se les suma una carga de −6μC a cada una de ellas?
Solución:
Dado que,
La primera carga, q 1 es +2μC.
La segunda carga, q 2 es +4μC.
La tercera carga, q 3 es -6μC.
La fuerza electrostática en el primer caso, F es de 20 N.
Por lo tanto,
F = kq 1 q 2 / r 2
o
20 N = k (+2 μC × +4 μC) / r 2 …… (1)
Ahora, cuando una tercera carga q3 se introduce en q1 y q2, las cargas en q1 y q2 cambian como:
q1′ = (2 – 6) μC = -4 μC
q2′ = (4 – 6) μC = -2 μC
Entonces, la fuerza electrostática en este nuevo caso es:
F’ = k q’ 1 q’ 2 / r 2
= k (-4 μC × -2 μC) / r 2 …… (2)
Ahora, para obtener F’, dividamos la ecuación (2) por (1) como,
F’ / 20 N = [k (-4 μC × -2 μC) / r2] / [20 N = k (+2 μC × +4 μC) / r 2 ]
F’ = +20 N
Por lo tanto, la fuerza electrostática cuando se introduce la tercera carga es de +20 N.
Problema 2: Determine la fuerza electrostática entre las dos cargas de magnitud 2 C y -1 C separadas por una distancia de 1 m en el aire.
Solución:
Dado que,
La primera carga, q1 es +2 C.
La segunda carga, q2 es -1C.
La distancia entre las dos cargas, r es de 1 m.
La fórmula para calcular la fuerza electrostática entre las cargas es:
F = kq 1 q 2 / r 2
Sustituya los valores dados en la expresión anterior como,
F = (9 × 10 9 Nm 2 / C 2 )(+2 C)(-1 C) / (1 m) 2
= 18 × 10 9 N
Problema 3: La distancia entre los dos electrones en contacto es igual a 1Å. Determine la fuerza de Coulomb entre ellos.
Solución:
La carga de un electrón, q es -1,6 × 10 -19 C.
La distancia entre las dos cargas, r es 1 Å.
La fórmula para calcular la fuerza electrostática entre los dos electrones es:
F = k (q 2 / r 2 )
Sustituya los valores dados en la expresión anterior como,
F = (9 × 10 9 Nm 2 / C 2 ) [(-1,6 × 10 -19 C) 2 / (1 Å) 2 ]
= 2,3 × 10 −8 N
Problema 4: Cuando se mantienen separados a cierta distancia, dos conductores esféricos B y C con radios similares y con cargas iguales se repelen con una fuerza F. Un tercer conductor esférico, con el mismo radio que B pero sin carga, se lleva a contacto con B, luego con C, y finalmente eliminado de ambos. ¿Cuál es la nueva fuerza de repulsión entre B y C?
Solución:
Para el caso dado,
Inicialmente, la fuerza electrostática sobre los conductores se define como:
F = k (q 2 / r 2 ) ……(1)
Pero cuando un tercer conductor esférico entra en contacto alternativamente con B y C entonces se retira, por lo que las cargas en B y C son Q/2 y 3Q/4 respectivamente.
Por lo tanto, la Nueva fuerza se convierte en:
F’ = k [Q / 2) (3Q / 4)/ r 2 ] ……(2)
Comparando la ecuación (1) y (2), obtenemos:
F’ = 38F
Problema 5: Considere un sistema de dos cargas de magnitud 2 × 10-7 C y 4,5 × 10-7 C sobre el que actúa una fuerza de 0,1 N. ¿Cuál es la distancia entre las dos cargas?
Solución:
Dado que,
La primera carga, q 1 es 2 × 10 -7 C.
La segunda carga, q 2 es 4.5 × 10 -7 C.
La fuerza que actuó sobre ellos, F es 0.1 N.
La fórmula para calcular la fuerza electrostática entre las cargas es:
F = kq 1 q 2 / r 2
Sustituya los valores dados en la expresión anterior como,
0,1 N = (9 × 10 9 Nm 2 / C 2 )(2 × 10 -7 C)(4,5 × 10 -7 C) / (r) 2
r = 0,09 m
Por tanto, la distancia entre las dos cargas, r, es de 0,9 m .
Problema 6: Determinar la magnitud de las dos cargas idénticas, cuando la fuerza electrostática entre estas dos cargas idénticas es de 1000 N y están separadas por una distancia de 0,1 m.
Solución:
Dado que,
La distancia entre las dos cargas, r es de 0,1 m.
La fuerza que actuó sobre ellos, F es 1000 N.
La fórmula para calcular la fuerza electrostática entre las cargas es:
F = kq 2 / r 2
donde q es la carga.
Reorganizar la fórmula anterior para q como,
q 2 = Fr 2 / k
Sustituya los valores dados en la expresión anterior como,
q 2 = (1000 N) (0,1 m) 2 / (9 × 10 9 Nm 2 / C 2 )
q = 0,33 × 10-5C
Por lo tanto, la magnitud de la carga es 0,33 × 10-5 C.
Problema 7: Considere dos cargas opuestas de la misma magnitud, colocadas a una distancia tal que la fuerza de FN actúe entre estas dos cargas. Si se transfiere el 60% del cargo de uno a otro. Determine cuánto cambia el valor de la fuerza en este caso.
Solución:
Inicialmente, la fuerza electrostática entre las dos cargas viene dada por,
F = kq 2 / r 2 ……(1)
Ahora, cuando se transfiere la carga, la fuerza electrostática se convierte en,
F’ = kq 1 q 2 / r 2 ……(2)
El cargo transferido es,
60 % de q = 60 / 100 × q = 3 / 5 q
Por lo tanto, carga q 1 = q – 3 / 5 q
= 2 / 5q
Y la carga q 2 = q + 3 / 5 q
= 8 / 5q
Por lo tanto, la fuerza neta entre estas cargas es,
F’ = kq 1 q 2 / r 2
= k (2 / 5 q) (8 / 5 q) / r 2
= 16 / 25 F
Problema 8: Una carga específica Q se divide en dos componentes, q y Qq. ¿Cuál es la relación entre Q y q si las dos porciones están separadas por r y tienen la mayor repulsión de Coulomb?
Solución:
Dado que, la carga Q dada se divide en cargas Qq y q separadas por una distancia r.
Sabemos,
F = kq 1 q 2 / r 2
es decir
F = kq (Qq) / r 2
Ahora, para maximizar esta fuerza, tomemos:
d F / dq = 0
lo que implica,
(Qq) – q = 0
2 q = Q
o
q = q / 2
Publicación traducida automáticamente
Artículo escrito por amanarora3dec y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA