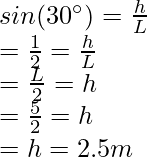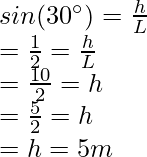En el uso diario, la palabra potencial se usa mucho para cosas o personas que prometen en su interior. “Potencial” muestra la posibilidad de acción. Da una idea de la energía almacenada que se puede convertir. Esta es la idea detrás de la energía potencial. Este concepto es parte integral de la mecánica y nos permite medir teóricamente la energía almacenada dentro de un objeto. La energía potencial puede venir a través de cualquier fuerza. Por ejemplo, un resorte estirado o comprimido tiene energía potencial. Un objeto que se encuentra a cierta altura posee energía potencial debido a la altura.
Energía potencial
La energía potencial es la energía que posee un objeto debido a su posición o configuración. Se dice que esta energía se almacena dentro del objeto. Por lo general, la energía potencial es liberada por un objeto por movimiento. Por ejemplo, un resorte estirado, cuando se suelta, comienza a moverse hacia su posición natural y comienza a adquirir velocidad. Debido a esta velocidad, adquiere energía cinética. Para comprender mejor esto, consideremos una bola de masa «m».
Esta pelota que inicialmente estaba en el suelo es llevada a una altura de “h”. Sobre él actúa una fuerza externa en forma de gravedad. Sabemos que el trabajo realizado por una fuerza F en un desplazamiento “s” sobre el objeto está dado por,
W = Fs
En este caso, la fuerza es la fuerza de la gravedad y el desplazamiento desde el suelo hasta la altura “h”.
F = mg, s = h
Entonces, el trabajo realizado por la gravedad sobre el objeto es,
W = -mgh
La energía potencial se define como el negativo de este trabajo. Denotando la energía potencial V(h).
V(h) = mgh
Si se deja caer la pelota, en ese caso, la energía potencial disminuye y la velocidad aumenta. Esto significa que la energía potencial del objeto se convierte en energía cinética. Digamos que la velocidad de la pelota justo antes de tocar el suelo es “v”.
![]()
Energía potencial en un resorte
Cuando el resorte se mantiene normalmente, se dice que tiene energía 0 y se dice que está en el estado de equilibrio. Cuando se estira o comprime, y hay un cierto desplazamiento, digamos x, tendrá cierta energía potencial guardada en él que se da como,
PE= 1/2 ( Kx2 )
Donde, K = constante de resorte
x = desplazamiento debido a compresión o expansión.
Veamos algunos problemas basados en estos conceptos.
Problemas de muestra
Pregunta 1: Una masa de 2Kg se toma del suelo a la altura de 10m. Encuentre la energía potencial del objeto.
Responder:
La energía potencial de una masa ‘m’ a la altura ‘h’ viene dada por,
P = mgh
Dado: m = 2 kg y g = 10 m/s 2 y h = 10 m.
Objetivo: encontrar la energía potencial.
Introduciendo los valores en la fórmula.
P = mgh
⇒ P = (2)(10)(10)
⇒P = 200J
Por lo tanto, la energía potencial del objeto es 200J.
Pregunta 2: Una masa de 5Kg se toma del suelo a la altura de 100m. Encuentre la energía potencial del objeto.
Responder:
La energía potencial de una masa ‘m’ a la altura ‘h’ viene dada por,
P = mgh
Dado: m = 5 kg y g = 10 m/s 2 y h = 100 m.
Objetivo: encontrar la energía potencial.
Introduciendo los valores en la fórmula.
P = mgh
⇒ P = (5)(10)(100)
⇒P = 5000J
Por lo tanto, la energía potencial del objeto es 5000J.
Pregunta 3: Una masa de 5 kg se toma del suelo durante 5 m cuesta arriba en la cuña. La cuña forma un ángulo de 30° con el suelo. Encuentre la energía potencial del bloque.
Responder:
La energía potencial de una masa ‘m’ a la altura ‘h’ viene dada por,
P = mgh
Esta cuña tiene la forma de un triángulo rectángulo.
Figura
Digamos que h es la altura vertical a la que llega la caja, sea L la longitud inclinada
largo = 5 metros
Dado: m = 5 kg y g = 10 m/s 2 y h = 2,5 m.
Objetivo: encontrar la energía potencial.
Introduciendo los valores en la fórmula.
P = mgh
⇒ P = (5)(10)(2.5)
⇒P = 125J
Por lo tanto, la energía potencial del objeto es 125J.
Pregunta 4: Una masa de 10 kg se toma del suelo durante 10 m cuesta arriba en la cuña. La cuña forma un ángulo de 30° con el suelo. Encuentre la energía potencial del bloque.
Responder:
La energía potencial de una masa ‘m’ a la altura ‘h’ viene dada por,
P = mgh
Esta cuña tiene la forma de un triángulo rectángulo.
Figura
Digamos que h es la altura vertical a la que llega la caja, sea L la longitud inclinada
largo = 10m
Dado: m = 5 kg y g = 10 m/s 2 y h = 5 m.
Objetivo: encontrar la energía potencial.
Introduciendo los valores en la fórmula.
P = mgh
⇒ P = (5)(10)(5)
⇒P = 250J
Por lo tanto, la energía potencial del objeto es 250J.
Pregunta 5: Encuentra la energía cinética de la pelota justo antes de tocar el suelo. Suponga que inicialmente la pelota estaba a una altura de 10 m y su masa era de 2 kg.
Responder:
Inicialmente, a la altura de 10 m, la pelota posee energía potencial. Cuando se deja caer, comienza a ir hacia el suelo y su altura comienza a disminuir. Al disminuir la altura, la velocidad aumenta y adquiere energía cinética.
Energía potencial en t = 0
La energía potencial estará dada por,
P = mgh
m = 2Kg, h = 10m y g = 10 m/s 2
P = mgh
⇒ P = (2)(10)(10)
⇒P = 200J
Cuando la pelota está a punto de tocar el suelo, su energía potencial se ha convertido en cero y toda la energía se convierte en energía cinética.
Por lo tanto, KE = 200J
Pregunta 6: Encuentra la velocidad de la pelota justo antes de tocar el suelo. Suponga que inicialmente la pelota estaba a una altura de 100 m y su masa era de 4 kg.
Responder:
Inicialmente, a la altura de 10 m, la pelota posee energía potencial. Cuando se deja caer, comienza a ir hacia el suelo y su altura comienza a disminuir. Al disminuir la altura, la velocidad aumenta y adquiere energía cinética.
Energía potencial en t = 0
La energía potencial estará dada por,
P = mgh
m = 4Kg, h = 100m y g = 10 m/s 2
P = mgh
⇒ P = (4)(100)(10)
⇒P = 4000J
Cuando la pelota está a punto de tocar el suelo, su energía potencial se ha convertido en cero y toda la energía se convierte en energía cinética.
Por lo tanto, KE = 4000J
La fórmula para KE es,
EC =
m = 4Kg y v = ?. Conectando los valores en la fórmula
EC =
⇒ 4000 =
⇒2000 = v2
⇒ v = 10√20 m/s
⇒ v = 20√5 m/s
Pregunta 7: Toda la energía potencial de una pelota se transforma en su energía cinética al caer al suelo desde cierta altura. La altura a la que se colocó inicialmente la pelota fue de 10 m. La masa de la pelota es de 1 kg. Encuentre la ganancia en la energía cinética.
Solución:
Dado que toda la energía potencial presente en la pelota se transfiere a su energía cinética,
Energía potencial de la pelota = Ganancia final en la energía cinética
P= mgh
m= 1kg, h= 10m, g= 9.8m/seg 2
P= 1× 10× 9.8
P= 98 julios
Por lo tanto, la ganancia final de energía cinética es de 98 julios.
KE= 98 julios.
Pregunta 8: Explique la existencia de energía potencial,
una. Por su posición
b. Por el estado en que se encuentra el objeto.
Responder:
La energía potencial en realidad puede estar presente en dos casos diferentes,
una. Por su posición
Supongamos que un objeto está estable en el suelo, ahora al aplicarle algo de energía, se toma a cierta altura. El objeto presente a cierta altura tendrá energía guardada en forma de energía potencial. Se da como,
PE= mgh
b. Por el estado en que se encuentra el objeto.
Cuando un resorte se mantiene en estado normal, se dice que tiene energía 0, pero cuando el mismo resorte se comprime o estira, obtiene energía potencial que se da como,
PE = 1/2 ( Kx2 )
Donde, x= desplazamiento, K= constante de resorte.
Pregunta 9: Un resorte se estira hasta 9 cm, la constante elástica del resorte es 2 N/m. ¿Encuentra el valor de la energía potencial almacenada en el resorte?
Solución:
La energía potencial almacenada en un resorte se da como,
PE= 1/2 ( Kx2 )
K= 2N/m, x= 9cm= 0.09m
PE= 1/2 (2× (0.09) 2 )
PE= 8,1 × 10 -3 julios.
Pregunta 10: Dos objetos se mantienen a diferentes alturas, el primer objeto está a 5 metros y el segundo objeto se coloca a 15 metros. ¿Qué objeto tiene más energía potencial si el primer objeto es 5 veces más pesado que el segundo?
Solución:
Objeto 1:
Altura= 5 m, Masa= 5 m
PE 1 = 5 m × 5 × 9,8
PE 1 = 245m julios.
Objeto 2:
Altura= 15 m, Masa= m
PE2 = 15× m× 9,8
PE 2 = 147 millones de julios.
Por tanto, aunque el primer objeto se mantenga a menor altura, debido a su peso, el primer objeto tiene más energía potencial.
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA