Requisito previo: diseñar un autómata finito
Supongamos que tenemos un DFA que está definido por ( Q, ![]() ,
, ![]() , q0, F ) y acepta el lenguaje L 1 . Entonces, el DFA que acepta el lenguaje L 2 donde L 2 = ̅L 1 ‘, se definirá como sigue:
, q0, F ) y acepta el lenguaje L 1 . Entonces, el DFA que acepta el lenguaje L 2 donde L 2 = ̅L 1 ‘, se definirá como sigue:
( Q,,
, q0, Q-F )
El complemento de un DFA se puede obtener haciendo que los estados no finales sean estados finales y viceversa . El idioma aceptado por el DFA L 2 complementado es el complemento del idioma L 1 .
Ejemplo-1:
L 1 : conjunto de todas las strings sobre {a, b} de longitud uniforme
L1 = {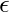 , ab, aa, abaa, aaba, ....}
, ab, aa, abaa, aaba, ....}
L 2 : conjunto de todas las strings sobre {a, b} de longitud impar
L2 = { a, b, aab, aaa, bba, bbb, ...}
Aquí, podemos ver que L 2 = ̅L 1
Primero dibujemos el DFA para L 1 que acepta las strings de longitud uniforme.

Ahora, para diseñar el DFA para L 2 , solo necesitamos complementar el DFA anterior. Cambiaremos los estados no finales por estados finales y los estados finales por estados no finales.

Este es nuestro DFA complementado requerido.
Ejemplo-2:
L 1 : conjunto de todas las strings sobre {a, b} que comienzan con ‘a’.
L1 ={ a, ab, aa, aba, aaa, aab, ..}
L 2 : conjunto de todas las strings sobre {a, b} que no comienzan con ‘a’.
L2 ={ 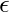 , b, ba, bb, bab, baa, bba, ...}
, b, ba, bb, bab, baa, bba, ...}
Aquí, podemos ver que L 2 = ̅L 1
Primero dibujemos el DFA para L 1 que acepta el conjunto de todas las strings sobre {a, b} comenzando con ‘a’

Ahora, para diseñar el DFA para L 2 , solo necesitamos complementar el DFA anterior. Cambiaremos los estados no finales por estados finales y los estados finales por estados no finales.

Este es nuestro DFA complementado requerido que acepta las strings que no comienzan con ‘a’.
Nota: Los lenguajes regulares están cerrados bajo el complemento (es decir, el complemento del lenguaje regular también será regular).
Publicación traducida automáticamente
Artículo escrito por SUDIPTADANDAPAT y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA