Proceso de Poisson homogéneo

El proceso de Poisson es uno de los procesos más importantes y ampliamente utilizados en la teoría de la probabilidad. Es ampliamente utilizado para modelar puntos aleatorios en el tiempo o el espacio. En este artículo discutiremos brevemente sobre el Proceso de Poisson homogéneo.

Proceso de Poisson:
aquí estamos derivando el proceso de Poisson como un proceso de conteo. Supongamos que estamos observando el número de ocurrencias de cierto evento durante un período de tiempo específico. (Aquí estamos considerando el tiempo como ejemplo. También podríamos considerar el espacio, etc.) Podemos considerar que ocurren bajo un Proceso de Poisson siempre que cumplan las siguientes condiciones.

El número de ocurrencias durante intervalos de tiempo disjuntos es independiente.
La probabilidad de una sola ocurrencia durante un pequeño intervalo de tiempo es proporcional a la longitud del intervalo.
Se puede despreciar la probabilidad de que ocurra más de una ocurrencia durante un pequeño intervalo de tiempo.

Si denotamos el número de ocurrencias durante un intervalo de tiempo de longitud t como X(t) entonces
$P(X(t)=n) = \frac{e^{-\lambda t}(\lambda t)^n}{n!}$

Ejemplos:
muchas situaciones de la vida real se pueden modelar utilizando el proceso de Poisson. Supongamos que consideramos el número de accidentes en una carretera. Podemos entender fácilmente que las tres condiciones anteriores se cumplen. Para dos intervalos de tiempo disjuntos, el número de accidentes en un camino dado es independiente. Nuevamente, es bastante improbable que ocurran dos o más accidentes en un pequeño intervalo de tiempo. Intuitivamente también podemos suponer que la probabilidad de que ocurra un accidente durante un pequeño intervalo de tiempo es proporcional a la duración del intervalo de tiempo. El número de terremotos en un lugar también se puede modelar mediante el proceso de Poisson.

Derivación:
ahora probamos nuestra afirmación de que si X(t) es el número de ocurrencias en un intervalo de longitud t, entonces, ¿
$P(X(t)=n) = \frac{e^{-\lambda t}(\lambda t)^n}{n!}$
dónde $\lambda$ está la tasa de ocurrencia?

Usaremos la inducción matemática para probar el enunciado. Primero escribimos las suposiciones escritas arriba en términos matemáticos. Según el supuesto 3 en un pequeño intervalo de tiempo h
$P(X(h) >1) = o(h)$
donde $\frac{o(h)}{h}$ tiende a cero cuando h tiende a cero o
$1-P(X(h)=0) -P(X(h)=1) = o(h)$ .
Nuevamente, si $\lambda$ es la tasa de ocurrencia, de acuerdo con la suposición 2 obtenemos,
$P(X(h)=1) =\lambda h$ .

Tomemos un intervalo (0, t) y un pequeño intervalo (t, t+h). Denotaremos P(X(t)=n) como $P_n(t)$ . Entonces, las ecuaciones anteriores se pueden escribir como,
$1-P_0(h) -P_1(h) = o(h)$
o
$P_0(h) = 1-\lambda h -o(h)$

Así que tenemos que probar eso
$P_n(t) = \frac{e^{-\lambda t}(\lambda t)^n}{n!}$ .
Primero probaremos el resultado para n=0 y n=1. Luego mostraremos que si el resultado es verdadero para n=m entonces será verdadero para n=m+1.

Tome el intervalo (0, t+h). Ahora,
$P_0(t+h)=P_0(t)P_0(h)$
(ya que las ocurrencias en el intervalo (0, t) y (t, t+h) son independientes) o ,
$P_0(t+h) = P_0(t)(1-\lambda (h) -o(h)$ o $\frac{P_0(t+h)-P_0(t)}{h} = -\lambda P_0(t) -\frac{o(h)}{h}$ .

Tomando límite cuando h tiende a cero obtenemos,
$P_{0}'(t) =- \lambda P_0(t).$ .
La solución de la ecuación diferencial anterior es,
$P_0(t)=ce^{-\lambda t}$ ,
tomando la condición inicial $P_0(0)=1$ evaluamos c=0. Por lo
$P_0(t)=e^{- \lambda t}$ tanto, nuestra afirmación es verdadera para n=0.

Ahora tratamos de demostrarlo para n=1.
$P_1(t+h)=P_1(t)P_0(h) + P_0(t)P_1(h)$
(Usamos el hecho de que la ocurrencia debe estar en cualquiera de los intervalos (0, t) y (t, t+h)), o
$P_1(t+h) =P_1(t)(1-\lambda h-o(h))+ e^{-\lambda t}(\lambda h)$ ,
o
$\frac{P_1(t+h) -P_1(t)}{h}= -\lambda P_1(t) - \lambda e^{-\lambda t}- \frac{o(h)}{h}$ .

Nuevamente tomando límite cuando h tiende a cero,
$P_{1}'(t)=-\lambda P_1(t) - \lambda e^{-\lambda t}$ .
Esta es una ecuación diferencial lineal de primer orden y la solución es,
$P_1(t)=\lambda t e^{-\lambda t}+c_1$
donde $c_1$ es una constante. Desde, $P_1(0)=0$ . Obtenemos,
$c_1=0$ . Por lo tanto $P_1(t)=\lambda t e^{-\lambda t}$ , o $P_1(t)=\frac{(\lambda t)^1 e^{-\lambda t}}{1!}$ .
Entonces nuestra afirmación es cierta para n=1. Suponemos que nuestra afirmación es cierta para n=m.

Mostraremos que es cierto para n=m+1. Entonces,
$P_{m+1}(t+h) =P_{m+1}(t)P_0(h) +P_m(t)P_1(h) +\sum_{j=1}^m {P_{m-j}(t)P_{j+1}(h)}$ (
Suponemos que la ocurrencia m+1 puede ocurrir de diferentes maneras, como m+1 ocurrencias en (0, t) y ninguna ocurrencia en (t, t+h) o m ocurrencias en (0, t) y 1. ocurrencia en (t, t+h), o mj ocurrencias en (0, t) y j+1 ocurrencia en (t, t+h) para j=1 a m). Entonces,
$P_{m+1}(t+h) =P_{m+1}(t)(1-\lambda h-o(h)) + \frac{e^{-\lambda t}(\lambda t)^m}{m!}\lambda h +\sum_{j=1}^m P_{m-j}(t)o(h)$
Dado que,
$P_{j+1}(h)=o(h)$ para j>=1.
O,
$\frac{P_{m+1}(t+h)-P_{m+1}(t)}{h}=-\lambda P_{m+1}(t)+\frac{{\lambda}^{m+1}t^m}{m!}e^{-\lambda t}+\frac{o(h)}{h}\sum_{j=1}^{m}P_{m-j}(t)-\frac{o_(h)}{h}P_{m+!}(t)$

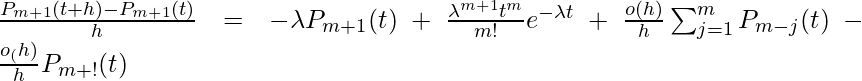
Tomando límite cuando h tiende a cero tenemos,
$P'_{m+1}(t)=-\lambda P_{m+1}(t) + \frac{{\lambda}^{m+1}t^m}{m!}e^{-\lambda t}$ .
Esta es nuevamente una ecuación diferencial de primer orden cuya solución es entonces,
$P_{m+1}(t)=\frac{(\lambda t)^{m+1}e^{-\lambda t}}{(m+1)!}+c_2$ .
Si asumimos que $P_{m+1}(0)=1$ obtenemos $c_2=0$ .

Así que el resultado final es,
$P_{m+1}(t)=\frac{(\lambda t)^{m+1}e^{-\lambda t}}{(m+1)!}$ .
Por lo tanto, el resultado está probado.

Por lo tanto, hemos derivado la pmf de no. de ocurrencias en un Proceso de Poisson que es una Distribución de Poisson con parámetro $\lambda$ . Ahora, si esto $\lambda$ es una función del tiempo, llamamos al proceso como proceso de Poisson no homogéneo .

Publicación traducida automáticamente

Artículo escrito por tufan_gupta2000 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta