Inversión de autómatas finitos deterministas

Requisito previo – Diseño de autómatas finitos  
Inversión: Definimos el lenguaje invertido   como el lenguaje  , donde 

Pasos para la reversión: 

1. Dibuja los estados tal como son.
2. Agregar un nuevo estado de aceptación único
3. Hacer que el estado de aceptación sea el estado inicial y el estado inicial el estado de aceptación
4. Invertir la función de transición en una relación de transición
5. Eliminar cualquier estado que ya no sea necesario

Nota : 

La inversión del autómata finito determinista da como resultado un autómata finito no determinista. Luego, esto se puede convertir en un autómata finito determinista mediante el algoritmo de conversión.

El proceso de inversión es así: 

Comprendamos el proceso de inversión en autómatas finitos deterministas (DFA) con la ayuda del siguiente ejemplo.

Ejemplo 1:

Proponemos un autómata finito determinista para el lenguaje de palabras que comienzan con el símbolo ‘a’:

Podemos construir el siguiente diagrama de transición de estado:

Ahora queremos construir el autómata finito que aceptará el reverso de este lenguaje,  .

Primero, agregamos un nuevo estado de aceptación único. Esto se debe a que eventualmente necesitaremos intercambiar los estados de aceptación e inicial, y solo puede haber un único estado inicial.

Luego, cambie los estados inicial y de aceptación:

Invierta la función de transición en una relación de transición:

Si bien esta es una solución válida, el Node marcado como C está colgando ya que no tiene bordes incidentes. Por lo tanto, se puede eliminar para dar un resultado final limpio:

Este autómata finito resultante es un autómata finito no determinista. Por lo tanto, el lenguaje invertido resultante es regular.

Explicación: 

1. Los mismos estados (A, B, C) se dibujan como presentes en un diagrama de estado original
2. Como A es el estado inicial, conviértalo en el estado final.
3. Como B es el estado final, conviértalo en el estado inicial.
4. Invirtiendo las aristas, ya que anteriormente las aristas apuntan A a B y A a C. Cambie la dirección, ahora los bordes apuntan hacia B hacia A y C hacia A.
5. Asigne los valores igual que el original.
6. Dibujar el bucle como en el diagrama de estado original
7. Como no hay borde incidente en el estado C, podemos reducir este estado C.
8. Dado que no hay transición para ‘a’ y ‘b’ en el estado A . Por lo tanto, la FA resultante es NFA.

Ejemplo 2: 
diseñar un DFA para el conjunto de strings sobre {a, b} de modo que la string del idioma contenga un número par de ‘a’. Se formará el idioma deseado: 

L1 = {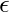, aa, aab, aba, aab, aababa, .......}

En L1, cada string tiene un número par de elementos a. 

Diagrama de transición de estado para el idioma L1: 

Este DFA acepta todas las strings que contienen un número par de elementos a. Aquí, el estado A es el estado inicial y el estado A es el estado final. Ahora, invirtiendo el idioma L1 que da el resultado final del idioma L2. 

Diagrama de transición de estado de L2 (inverso de L1): 

Así, vemos que L2 se ha obtenido a través del proceso de reversión y este DFA final acepta todas las strings que contienen un número par del elemento a que es el mismo que el idioma original.  

L2 = {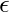, aa, aab, aba, aab, aababa, .......}

Explicación: 

1. Los mismos estados (A, B) se dibujan como presentes en un diagrama de estado original.
2. Como A es el estado inicial, conviértalo en el estado final.
3. Como A es el estado final, conviértalo en el estado inicial.
4. Invirtiendo las aristas, ya que anteriormente las aristas apuntan de A a B y así sucesivamente. Cambie la dirección, ahora los bordes apuntan hacia B a A y así sucesivamente.
5. Asigne los valores igual que el original.
6. Dado que hay una transición para ‘a’ y ‘b’ en los estados A y B, la resultante FA es DFA.
7. Dado que el diagrama de estado antes y después de la inversión es el mismo. Por lo tanto L1 = L2