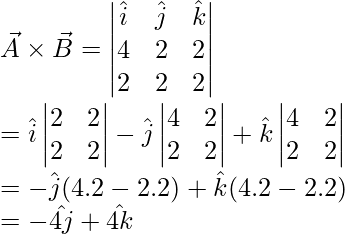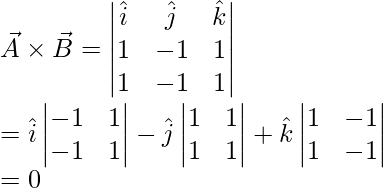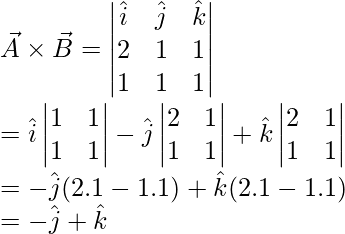Las operaciones vectoriales se utilizan en casi todas partes en el campo de la física. Muchas veces estas operaciones incluyen sumas, restas y multiplicaciones. La suma y la resta se pueden realizar usando la ley del triángulo de la suma de vectores. En el caso de los productos, la multiplicación de vectores se puede hacer de dos maneras, ya sea productos escalares o productos vectoriales. Los productos vectoriales dan el vector como producto resultante después de la multiplicación. En el movimiento de rotación, muchas cantidades se derivan utilizando productos vectoriales. Se vuelve esencial comprender los conceptos y la intuición detrás de este producto. Veamos este producto en detalle.
Producto de Vectores
En el caso de la multiplicación vectorial, existen básicamente dos tipos de productos: escalar y vectorial. El producto escalar es un tipo de multiplicación que da como resultado una cantidad escalar. El producto cruzado es un tipo de multiplicación que da como resultado una cantidad vectorial. Los productos vectoriales se utilizan para definir otras cantidades vectoriales derivadas. Las ecuaciones para el par, la velocidad angular y la aceleración. Todas estas cantidades involucran las operaciones que dan como resultado vectores a partir de vectores. Estas operaciones suelen ser productos vectoriales.
Producto escalar
Considere dos vectores y . El producto escalar de estos dos vectores está definido por la ecuación, ![]()
![]()
![]()
Aquí,
Considere dos vectores \vec{A} y \vec{B}. El producto vectorial de estos dos vectores se denota por ![]() . La dirección de este vector es perpendicular a ambos vectores. La magnitud de este vector está dada por,
. La dirección de este vector es perpendicular a ambos vectores. La magnitud de este vector está dada por,
![]()
Aquí,
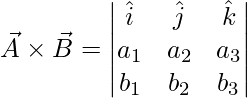
la
![]()
En este caso, la magnitud de ambos productos será la misma pero la dirección será completamente opuesta. Esto significa,
![]()
![]()
Problemas de muestra
Pregunta 1: Dos vectores están dados por, a = 2i + j + k y b = i + j + k. Encuentra el producto escalar de estos dos vectores.
Responder:
Dado:
a = 2i + j + k
segundo = yo + j + k
abdominales
⇒ (2i + j + k ).( i + j + k )
⇒ 2,1 + 1,1 + 1,1
⇒ 4
Pregunta 2: Dos vectores están dados por, a = i + j + k y b = i – 2j + 3k. Encuentra el producto escalar de estos dos vectores.
Responder:
Dado:
a = yo + j + k
b = yo -2j + 3k
abdominales
⇒ (i + j + k ).( i – 2j + 3k )
⇒ 1.1 – 2.1 + 1.3
⇒ 1 – 2 + 3
⇒ 2
Pregunta 3: Dos vectores están dados por, a = 4i +2 j +2 k y b = 2i + 2j + 2k. Encuentra el producto cruz de estos dos vectores.
Responder:
Dado:
a = 4i + 2j + 2k
b = 2i + 2j + 2k
Pregunta 4: Dos vectores están dados por, a = i – j + k y b = i – j + k. Encuentre el producto cruzado de estos dos vectores.
Responder:
Dado:
a = yo – j + k
b = yo – j + k
Pregunta 5: Dos vectores están dados por, a = j + 4k yb = 5i +4j + 3k. Calcula c = axb + bx a.
Responder:
Dado:
a = j + 4k
b = 5i + 4j + 3k
Sea el vector resultante c,
c = axb + bxa … (1)
Como se mencionó en las propiedades anteriores, el producto vectorial no es de naturaleza conmutativa.
Pero esto se puede reescribir,
Usando estos valores en la ecuación (1)
c = axb + bxa
⇒ c = – (bxa) + bxa
⇒ c = 0
Pregunta 6: Dos vectores están dados por, a = 2i + j + k y b = i + j + k. Encuentra el producto cruz de estos dos vectores.
Responder:
Dado:
a = 2i + j + k
segundo = yo + j + k
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA