Producto mínimo de k enteros en una array de enteros positivos

Dada una array de n enteros positivos. Estamos obligados a escribir un programa para imprimir el producto mínimo de k enteros de la array dada.

Ejemplos: 

Input : 198 76 544 123 154 675
         k = 2
Output : 9348
We get minimum product after multiplying
76 and 123.

Input : 11 8 5 7 5 100
        k = 4
Output : 1400

La idea es simple, encontramos los elementos k más pequeños e imprimimos la multiplicación de ellos. En la implementación a continuación, hemos utilizado un enfoque simple basado en Heap donde insertamos elementos de array en un mini-heap y luego encontramos el producto de los k elementos principales.

Diagrama de flujo:

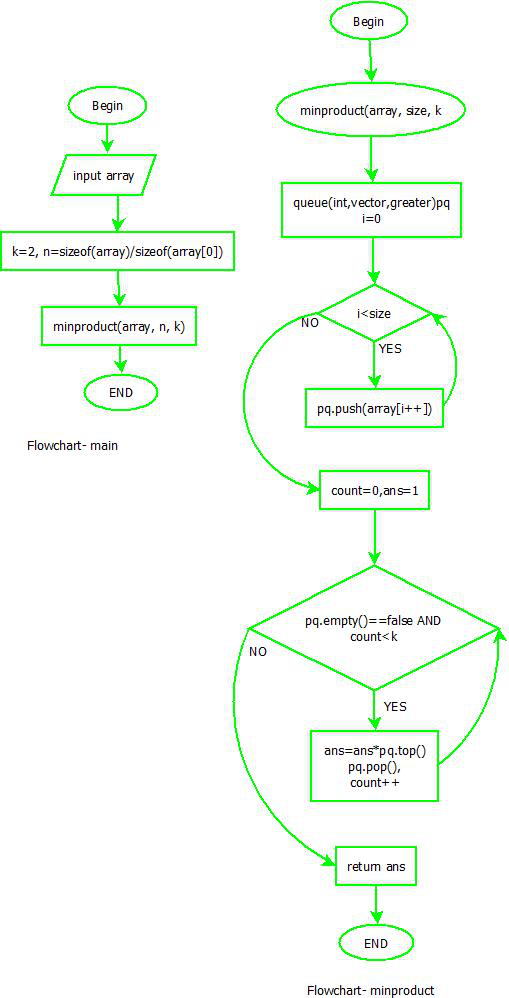
diagrama de flujo

Implementación:

// CPP program to find minimum product of
// k elements in an array
#include <bits/stdc++.h>
using namespace std;
 
int minProduct(int arr[], int n, int k)
{
    priority_queue<int, vector<int>, greater<int> > pq;
    for (int i = 0; i < n; i++)
        pq.push(arr[i]);
 
    int count = 0, ans = 1;
 
    // One by one extract items from max heap
    while (pq.empty() == false && count < k) {
        ans = ans * pq.top();
        pq.pop();
        count++;
    }
 
    return ans;
}
 
// Driver code
int main()
{
    int arr[] = { 198, 76, 544, 123, 154, 675 };
    int k = 2;
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << "Minimum product is " << minProduct(arr, n, k);
    return 0;
}

// Java program to find minimum product of
// k elements in an array
 
import java.util.PriorityQueue;
 
class GFG
{
    public static int minProduct(int[] arr, int n, int k)
    {
        PriorityQueue<Integer> pq = new PriorityQueue<>();
        for (int i = 0; i < n; i++)
            pq.add(arr[i]);
         
            int count = 0, ans = 1;
 
            // One by one extract items
            while(pq.isEmpty() == false && count < k)
            {
                ans = ans * pq.element();
                pq.remove();
                count++;
            }
         
            return ans;
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int arr[] = {198, 76, 544, 123, 154, 675};
        int k = 2;
        int n = arr.length;
        System.out.print("Minimum product is " +
                          minProduct(arr, n, k));
    }
}
 
// This code is contributed by sanjeev2552

# Python3 program to find minimum
# product of k elements in an array
 
import math
import heapq
 
def minProduct(arr, n, k):
 
    heapq.heapify(arr)
    count = 0
    ans = 1
 
    # One by one extract
    # items from min heap
    while ( arr ) and count < k:
        x = heapq.heappop(arr)
        ans = ans * x
        count = count + 1
     
    return ans;
 
# Driver method
arr = [198, 76, 544, 123, 154, 675]
k = 2
n = len(arr)
print ("Minimum product is",
       minProduct(arr, n, k))

// C# program to find minimum product of
// k elements in an array
 
using System;
using System.Collections.Generic;
public class GFG
{
  public static int minProduct(int[] arr, int n, int k)
  {
    List<int> pq = new List<int>();
    for (int i = 0; i < n; i++)
      pq.Add(arr[i]);
 
    int count = 0, ans = 1;
 
    // One by one extract items
    while(pq.Count!=0 && count < k)
    {
      pq.Sort();
      ans = ans * pq[0];
      pq.RemoveAt(0);
      count++;
    }
 
    return ans;
  }
 
  // Driver Code
  public static void Main(String[] args)
  {
    int []arr = {198, 76, 544, 123, 154, 675};
    int k = 2;
    int n = arr.Length;
    Console.Write("Minimum product is " +
                  minProduct(arr, n, k));
  }
}
 
// This code is contributed by Rajput-Ji

<script>
 
// Javascript program to find minimum product of
// k elements in an array
 
function minProduct(arr, n, k) {
    let pq = new Array();
    for (let i = 0; i < n; i++)
        pq.push(arr[i]);
 
    let count = 0, ans = 1;
 
    // One by one extract items
    while (pq.length != 0 && count < k) {
        pq.sort((a, b) => a - b);
        ans = ans * pq[0];
        pq.shift(0);
        count++;
    }
 
    return ans;
}
 
// Driver Code
 
let arr = [198, 76, 544, 123, 154, 675];
let k = 2;
let n = arr.length;
document.write("Minimum product is " + minProduct(arr, n, k));
 
 
// This code is contributed by Saurabh Jaiswal
</script>

Minimum product is 9348

Complejidad de tiempo: O(n * log n), 
Espacio auxiliar: O(n) para cola de prioridad

Nota: El problema anterior se puede resolver en tiempo O(n) usando los métodos discutidos aquí y aquí .

Este artículo es una contribución de Gitanjali Sharma . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.