Programa C para buscar un elemento en una array ordenada y rotada

Un elemento en una array ordenada se puede encontrar en el tiempo O (log n) a través de una búsqueda binaria . Pero supongamos que rotamos una array ordenada de orden ascendente en algún pivote desconocido para usted de antemano. Entonces, por ejemplo, 1 2 3 4 5 podría convertirse en 3 4 5 1 2. Inventa una forma de encontrar un elemento en el arreglo rotado en tiempo O(log n).
 

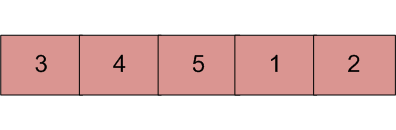
Ejemplo: 
 

Input  : arr[] = {5, 6, 7, 8, 9, 10, 1, 2, 3};
         key = 3
Output : Found at index 8

Input  : arr[] = {5, 6, 7, 8, 9, 10, 1, 2, 3};
         key = 30
Output : Not found

Input : arr[] = {30, 40, 50, 10, 20}
        key = 10   
Output : Found at index 3

Todas las soluciones proporcionadas aquí asumen que todos los elementos de la array son distintos.
Solución básica: 
Enfoque: 
 

1. La idea es encontrar el punto de pivote, dividir la array en dos sub-arrays y realizar una búsqueda binaria.
2. La idea principal para encontrar el pivote es: para una array ordenada (en orden creciente) y pivotada, el elemento pivote es el único elemento para el que el siguiente elemento es más pequeño que él.
3. Usando la declaración anterior y el pivote de búsqueda binaria se puede encontrar.
4. Después de encontrar el pivote, divida la array en dos sub-arrays.
5. Ahora los subconjuntos individuales se ordenan para que el elemento se pueda buscar mediante la búsqueda binaria.

Implementación: 
 

Input arr[] = {3, 4, 5, 1, 2}
Element to Search = 1
  1) Find out pivot point and divide the array in two
      sub-arrays. (pivot = 2) /*Index of 5*/
  2) Now call binary search for one of the two sub-arrays.
      (a) If element is greater than 0th element then
             search in left array
      (b) Else Search in right array
          (1 will go in else as 1 < 0th element(3))
  3) If element is found in selected sub-array then return index
     Else return -1.

A continuación se muestra la implementación del enfoque anterior: 
 

/* Program to search an element in 
   a sorted and pivoted array*/
#include <stdio.h>
  
int findPivot(int[], int, int);
int binarySearch(int[], int, int, int);
  
/* Searches an element key in a pivoted 
   sorted array arrp[] of size n */
int pivotedBinarySearch(int arr[], int n, int key)
{
    int pivot = findPivot(arr, 0, n - 1);
  
    // If we didn't find a pivot, 
// then array is not rotated at all
    if (pivot == -1)
        return binarySearch(arr, 0, n - 1, key);
  
    // If we found a pivot, then first 
// compare with pivot and then
    // search in two subarrays around pivot
    if (arr[pivot] == key)
        return pivot;
    if (arr[0] <= key)
        return binarySearch(arr, 0, pivot - 1, key);
    return binarySearch(arr, pivot + 1, n - 1, key);
}
  
/* Function to get pivot. For array 
   3, 4, 5, 6, 1, 2 it returns 3 (index of 6) */
int findPivot(int arr[], int low, int high)
{
    // base cases
    if (high < low)
        return -1;
    if (high == low)
        return low;
  
    int mid = (low + high) / 2; /*low + (high - low)/2;*/
    if (mid < high && arr[mid] > arr[mid + 1])
        return mid;
    if (mid > low && arr[mid] < arr[mid - 1])
        return (mid - 1);
    if (arr[low] >= arr[mid])
        return findPivot(arr, low, mid - 1);
    return findPivot(arr, mid + 1, high);
}
  
/* Standard Binary Search function*/
int binarySearch(int arr[], int low, int high, int key)
{
    if (high < low)
        return -1;
    int mid = (low + high) / 2; /*low + (high - low)/2;*/
    if (key == arr[mid])
        return mid;
    if (key > arr[mid])
        return binarySearch(arr, (mid + 1), high, key);
    return binarySearch(arr, low, (mid - 1), key);
}
  
/* Driver program to check above functions */
int main()
{
    // Let us search 3 in below array
    int arr1[] = { 5, 6, 7, 8, 9, 10, 1, 2, 3 };
    int n = sizeof(arr1) / sizeof(arr1[0]);
    int key = 3;
    printf("Index of the element is : %d",
           pivotedBinarySearch(arr1, n, key));
    return 0;
}

Producción: 
 

Index of the element is : 8

Análisis de Complejidad: 
 

• Complejidad temporal: O(log n). 
  La búsqueda binaria requiere comparaciones log n para encontrar el elemento. Entonces la complejidad del tiempo es O (log n).
• Complejidad espacial: O(1), No se requiere espacio adicional.

Consulte el artículo completo sobre Buscar un elemento en una array ordenada y rotada para obtener más detalles.