Dada una string de expresión exp, escriba un programa para examinar si los pares y los órdenes de “{“, “}”, “(“, “)”, “[“, “]” son correctos en exp.
Ejemplo :
Entrada : exp = “[()]{}{[()()]()}”
Salida : BalanceadaEntrada : exp = “[(])”
Salida : No balanceada
Algoritmo:
- Declara una pila de caracteres S.
- Ahora recorra la string de expresión exp.
- Si el carácter actual es un corchete de inicio ( ‘(‘ o ‘{‘ o ‘[‘ ) entonces empújelo para apilar.
- Si el carácter actual es un corchete de cierre ( ‘)’ o ‘}’ o ‘]’ ), entonces salte de la pila y si el carácter reventado es el corchete de inicio correspondiente, entonces bien, de lo contrario, los corchetes no están equilibrados.
- Después de completar el recorrido, si queda algún soporte inicial en la pila, entonces «no está equilibrado»
La imagen de abajo es una ejecución en seco del enfoque anterior:
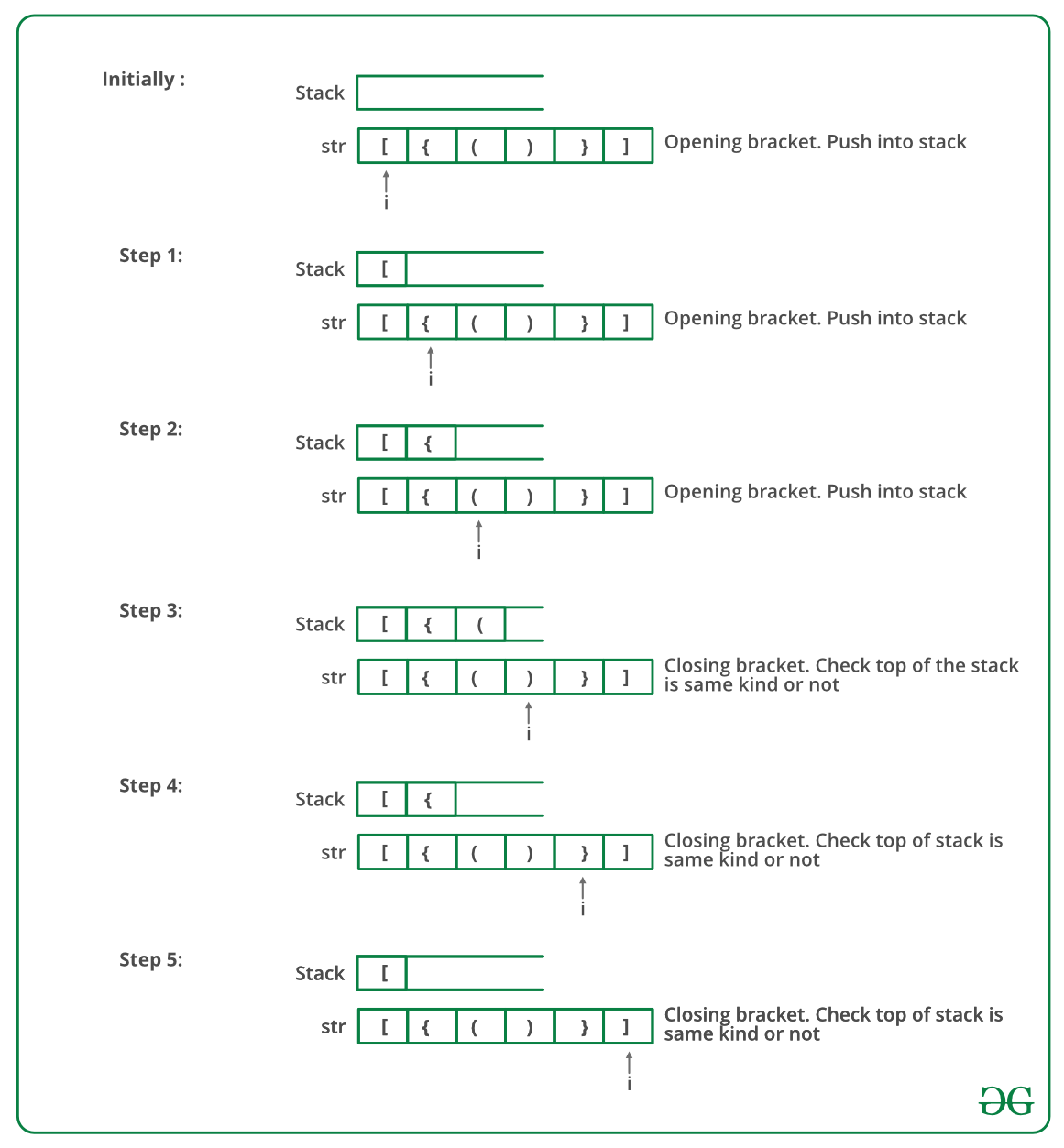
A continuación se muestra la implementación del enfoque anterior:
C#
// C# program for checking
// balanced Brackets
using System;
using System.Collections.Generic;
public class BalancedBrackets {
public class stack {
public int top = -1;
public char[] items = new char[100];
public void push(char x)
{
if (top == 99)
{
Console.WriteLine("Stack full");
}
else {
items[++top] = x;
}
}
char pop()
{
if (top == -1)
{
Console.WriteLine("Underflow error");
return '�';
}
else
{
char element = items[top];
top--;
return element;
}
}
Boolean isEmpty()
{
return (top == -1) ? true : false;
}
}
// Returns true if character1 and character2
// are matching left and right brackets */
static Boolean isMatchingPair(char character1,
char character2)
{
if (character1 == '(' && character2 == ')')
return true;
else if (character1 == '{' && character2 == '}')
return true;
else if (character1 == '[' && character2 == ']')
return true;
else
return false;
}
// Return true if expression has balanced
// Brackets
static Boolean areBracketsBalanced(char[] exp)
{
// Declare an empty character stack */
Stack<char> st = new Stack<char>();
// Traverse the given expression to
// check matching brackets
for (int i = 0; i < exp.Length; i++)
{
// If the exp[i] is a starting
// bracket then push it
if (exp[i] == '{' || exp[i] == '('
|| exp[i] == '[')
st.Push(exp[i]);
// If exp[i] is an ending bracket
// then pop from stack and check if the
// popped bracket is a matching pair
if (exp[i] == '}' || exp[i] == ')'
|| exp[i] == ']') {
// If we see an ending bracket without
// a pair then return false
if (st.Count == 0)
{
return false;
}
// Pop the top element from stack, if
// it is not a pair brackets of
// character then there is a mismatch. This
// happens for expressions like {(})
else if (!isMatchingPair(st.Pop(),
exp[i])) {
return false;
}
}
}
// If there is something left in expression
// then there is a starting bracket without
// a closing bracket
if (st.Count == 0)
return true; // balanced
else
{
// not balanced
return false;
}
}
// Driver code
public static void Main(String[] args)
{
char[] exp = { '{', '(', ')', '}', '[', ']' };
// Function call
if (areBracketsBalanced(exp))
Console.WriteLine("Balanced ");
else
Console.WriteLine("Not Balanced ");
}
}
// This code is contributed by 29AjayKumar
Balanced
Complejidad de Tiempo: O(n)
Espacio Auxiliar: O(n) para pila.
¡Consulte el artículo completo sobre Verificación de paréntesis equilibrados en una expresión (bien formado) usando Stack para obtener más detalles!
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA