Requisito previo: Comparación entre clasificación por burbuja, clasificación por inserción y clasificación por selección.
Escriba un programa en C para trazar y analizar la complejidad temporal de la clasificación por burbujas , la clasificación por inserción y la clasificación por selección (usando Gnuplot).
Según el problema, tenemos que trazar un gráfico de complejidad de tiempo simplemente usando C. Por lo tanto, haremos algoritmos de clasificación como funciones y todos los algoritmos se proporcionan para clasificar exactamente la misma array para mantener la comparación justa.
Ejemplos:
Input: randomly generated arrays (using rand() function) of different sizes as input for sorting. Output: A_size, Bubble, Insertion, Selection 10000, 366263, 80736, 152975 20000, 1594932, 332101, 609388 30000, 3773121, 785790, 1441547 40000, 7174455, 1574855, 2620006 50000, 10917061, 2029586, 4025993 60000, 15484338, 2998403, 5556494 70000, 21201561, 4146680, 7678139 80000, 29506758, 6027335, 10131950 90000, 36457272, 6699452, 12436376 100000, 43472313, 8335881, 15208712
Enfoque: utilizaremos arrays de diferentes tamaños para trazar el gráfico entre el tiempo que tarda el algoritmo de clasificación y el tamaño de la array. La ejecución del programa llevará algún tiempo para clasificar arrays de tamaño de hasta 100000 elementos.
A continuación se muestra la implementación del enfoque anterior:
// C program to store time taken by bubble sort,
// insertion sort and selection sort
// for sorting exactly same arrays.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// Swap utility
void swap(long int* a, long int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
// Bubble sort
void bubbleSort(long int a[], long int n)
{
for (long int i = 0; i < n - 1; i++) {
for (long int j = 0; j < n - 1 - i; j++) {
if (a[j] > a[j + 1]) {
swap(&a[j], &a[j + 1]);
}
}
}
}
// Insertion sort
void insertionSort(long int arr[], long int n)
{
long int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
// Move elements of arr[0..i-1], that are
// greater than key, to one position ahead
// of their current position
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// Selection sort
void selectionSort(long int arr[], long int n)
{
long int i, j, midx;
for (i = 0; i < n - 1; i++) {
// Find the minimum element in unsorted array
midx = i;
for (j = i + 1; j < n; j++)
if (arr[j] < arr[min_idx])
midx = j;
// Swap the found minimum element
// with the first element
swap(&arr[midx], &arr[i]);
}
}
// Driver code
int main()
{
long int n = 10000;
int it = 0;
// Arrays to store time duration
// of sorting algorithms
double tim1[10], tim2[10], tim3[10];
printf("A_size, Bubble, Insertion, Selection\n");
// Performs 10 iterations
while (it++ < 10) {
long int a[n], b[n], c[n];
// generating n random numbers
// storing them in arrays a, b, c
for (int i = 0; i < n; i++) {
long int no = rand() % n + 1;
a[i] = no;
b[i] = no;
c[i] = no;
}
// using clock_t to store time
clock_t start, end;
// Bubble sort
start = clock();
bubbleSort(a, n);
end = clock();
tim1[it] = ((double)(end - start));
// Insertion sort
start = clock();
insertionSort(b, n);
end = clock();
tim2[it] = ((double)(end - start));
// Selection sort
start = clock();
selectionSort(c, n);
end = clock();
tim3[it] = ((double)(end - start));
// type conversion to long int
// for plotting graph with integer values
printf("%li, %li, %li, %li\n",
n,
(long int)tim1[it],
(long int)tim2[it],
(long int)tim3[it]);
// increases the size of array by 10000
n += 10000;
}
return 0;
}
Producción:
A_size, Bubble, Insertion, Selection 10000, 366263, 80736, 152975 20000, 1594932, 332101, 609388 30000, 3773121, 785790, 1441547 40000, 7174455, 1574855, 2620006 50000, 10917061, 2029586, 4025993 60000, 15484338, 2998403, 5556494 70000, 21201561, 4146680, 7678139 80000, 29506758, 6027335, 10131950 90000, 36457272, 6699452, 12436376 100000, 43472313, 8335881, 15208712
Ahora viene la pregunta de ¿cómo vamos a trazar un gráfico en coordenadas xy?
Para eso, usaremos una utilidad muy simple llamada Gnuplot .
Gnuplot es una utilidad gráfica portátil impulsada por línea de comandos para Linux, MS Windows, OSX y muchas otras plataformas.
Nota: En este artículo, se usa Ubuntu (Linux).
- Lo primero es lo primero: cómo instalar Gnuplot. Use este comando para instalar Gnuplot.
sudo apt-get install gnuplot
- Después de esto, compile su código y copie la salida en un archivo de texto usando este comando.
./a.out>plot.txt
- Abra Gnuplot simplemente usando.
gnuplot
- Ahora lo último es trazar el gráfico, así que use este comando para trazar el gráfico de complejidad.
plot './plot.txt' using 1:2 with linespoints, './plot.txt' using 1:3 with linespoints, './plot.txt' using 1:4 with linespoints
Aquí hay un complemento de terminal de comandos.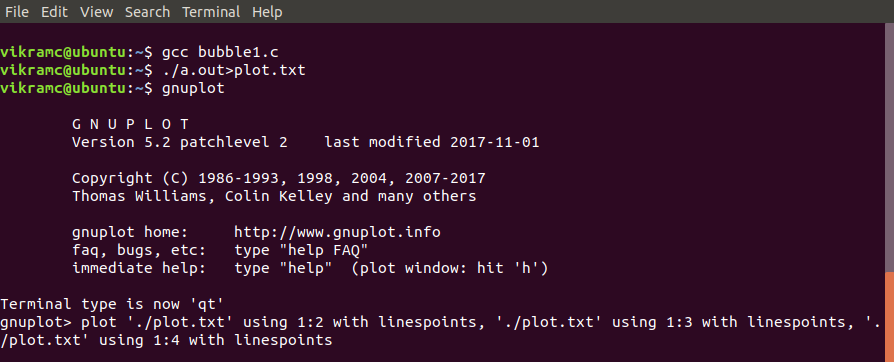
Aquí está el gráfico de complejidad que compara la clasificación de burbuja (curva púrpura), la clasificación de inserción (curva verde) y la clasificación de selección (curva azul).
Observación:
la complejidad temporal promedio de los tres algoritmos es O(n^2) , pero a medida que aumenta el tamaño de los datos de entrada, la ordenación por inserción funciona mucho mejor que la ordenación por burbuja y ligeramente mejor que la ordenación por selección.