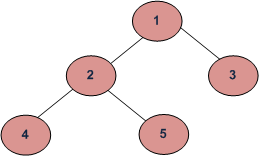
El tamaño de un árbol es el número de elementos presentes en el árbol. El tamaño del árbol de abajo es 5.
C++
// C++ program to print size of tree in iterative
#include<iostream>
#include<queue>
using namespace std;
struct Node
{
int data;
Node *left, *right;
};
// A utility function to
// create a new Binary Tree Node
Node *newNode(int data)
{
Node *temp = new Node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
// return size of tree
int sizeoftree(Node *root)
{
// if tree is empty it will
// return 0
if(root == NULL)
return 0;
// Using level order Traversal.
queue<Node *> q;
int count = 1;
q.push(root);
while(!q.empty())
{
Node *temp = q.front();
if(temp->left)
{
// Enqueue left child
q.push(temp->left);
// Increment count
count++;
}
if(temp->right)
{
// Enqueue right child
q.push(temp->right);
// Increment count
count++;
}
q.pop();
}
return count;
}
// Driver Code
int main()
{
Node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Size of the tree is " <<
sizeoftree(root) << endl;
return 0;
}
// This code is contributed by SHAKEELMOHAMMAD
Java
// Java programn to calculate
// Size of a tree
import java.util.LinkedList;
import java.util.Queue;
class Node
{
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree
{
Node root;
public int size()
{
if (root == null)
return 0;
// Using level order Traversal.
Queue<Node> q = new LinkedList<Node>();
q.offer(root);
int count = 1;
while (!q.isEmpty())
{
Node tmp = q.poll();
// when the queue is empty:
// the poll() method returns null.
if (tmp != null)
{
if (tmp.left != null)
{
// Increment count
count++;
// Enqueue left child
q.offer(tmp.left);
}
if (tmp.right != null)
{
// Increment count
count++;
// Enqueue left child
q.offer(tmp.right);
}
}
}
return count;
}
public static void main(String args[])
{
/* creating a binary tree and entering
the nodes */
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("The size of binary tree" +
" is : " + tree.size());
}
}
Python3
# Python Program to calculate size of the tree iteratively # Node Structure class newNode: def __init__(self,data): self.data = data self.left = self.right = None # Return size of tree def sizeoftree(root): if root == None: return 0 q = [] q.append(root) count = 1 while(len(q) != 0): root = q.pop(0) if(root.left): q.append(root.left) count += 1 if(root.right): q.append(root.right) count += 1 return count # Driver Program root = newNode(1) root.left = newNode(2) root.right = newNode(3) root.left.left = newNode(4) root.left.right = newNode(5) print(sizeoftree(root)) # This is code is contributed by simranjenny84
C#
// C# programn to calculate
// Size of a tree
using System;
using System.Collections.Generic;
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
Node root;
public int size()
{
if (root == null)
return 0;
// Using level order Traversal.
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
int count = 1;
while (q.Count != 0)
{
Node tmp = q.Dequeue();
// when the queue is empty:
// the poll() method returns null.
if (tmp != null)
{
if (tmp.left != null)
{
// Increment count
count++;
// Enqueue left child
q.Enqueue(tmp.left);
}
if (tmp.right != null)
{
// Increment count
count++;
// Enqueue left child
q.Enqueue(tmp.right);
}
}
}
return count;
}
// Driver code
public static void Main(String []args)
{
/* creating a binary tree and entering
the nodes */
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("The size of binary tree" +
" is : " + tree.size());
}
}
// This code has been contributed by 29AjayKumar
Javascript
<script>
// JavaScript programn to calculate Size of a tree
class Node
{
constructor(item) {
this.left = null;
this.right = null;
this.data = item;
}
}
let root;
function size()
{
if (root == null)
return 0;
// Using level order Traversal.
let q = [];
q.push(root);
let count = 1;
while (q.length > 0)
{
let tmp = q[0];
q.shift();
// when the queue is empty:
// the poll() method returns null.
if (tmp != null)
{
if (tmp.left != null)
{
// Increment count
count++;
// Enqueue left child
q.push(tmp.left);
}
if (tmp.right != null)
{
// Increment count
count++;
// Enqueue left child
q.push(tmp.right);
}
}
}
return count;
}
/* creating a binary tree and entering
the nodes */
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
document.write("Size of the tree is " + size());
</script>
Publicación traducida automáticamente
Artículo escrito por Ashi Singh y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA