Programa Javascript para el subarreglo contiguo de suma más grande

Escriba un programa eficiente para encontrar la suma de subarreglo contiguo dentro de un arreglo unidimensional de números que tenga la suma más grande. 

Algoritmo de Kadane:

Initialize:
    max_so_far = INT_MIN
    max_ending_here = 0

Loop for each element of the array
  (a) max_ending_here = max_ending_here + a[i]
  (b) if(max_so_far < max_ending_here)
            max_so_far = max_ending_here
  (c) if(max_ending_here < 0)
            max_ending_here = 0
return max_so_far

Explicación: 
la idea simple del algoritmo de Kadane es buscar todos los segmentos contiguos positivos de la array (para esto se usa max_ending_here). Y realice un seguimiento de la suma máxima de segmentos contiguos entre todos los segmentos positivos (para esto se usa max_so_far). Cada vez que obtengamos una suma positiva, compárela con max_so_far y actualice max_so_far si es mayor que max_so_far 

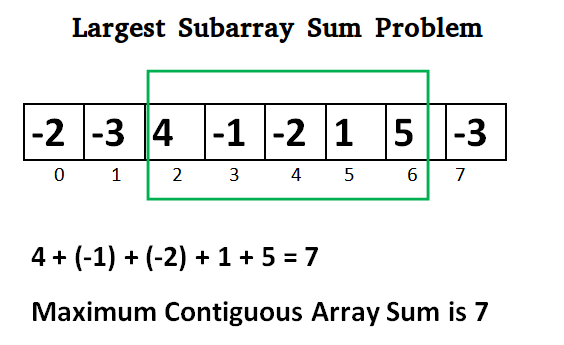
    Lets take the example:
    {-2, -3, 4, -1, -2, 1, 5, -3}

    max_so_far = max_ending_here = 0

    for i=0,  a[0] =  -2
    max_ending_here = max_ending_here + (-2)
    Set max_ending_here = 0 because max_ending_here < 0

    for i=1,  a[1] =  -3
    max_ending_here = max_ending_here + (-3)
    Set max_ending_here = 0 because max_ending_here < 0

    for i=2,  a[2] =  4
    max_ending_here = max_ending_here + (4)
    max_ending_here = 4
    max_so_far is updated to 4 because max_ending_here greater 
    than max_so_far which was 0 till now

    for i=3,  a[3] =  -1
    max_ending_here = max_ending_here + (-1)
    max_ending_here = 3

    for i=4,  a[4] =  -2
    max_ending_here = max_ending_here + (-2)
    max_ending_here = 1

    for i=5,  a[5] =  1
    max_ending_here = max_ending_here + (1)
    max_ending_here = 2

    for i=6,  a[6] =  5
    max_ending_here = max_ending_here + (5)
    max_ending_here = 7
    max_so_far is updated to 7 because max_ending_here is 
    greater than max_so_far

    for i=7,  a[7] =  -3
    max_ending_here = max_ending_here + (-3)
    max_ending_here = 4

Programa: 

<script>
 
// JavaScript program to find maximum
// contiguous subarray
  
// Function to find the maximum
// contiguous subarray
function maxSubArraySum(a, size)
{
    var maxint = Math.pow(2, 53)
    var max_so_far = -maxint - 1
    var max_ending_here = 0
      
    for (var i = 0; i < size; i++)
    {
        max_ending_here = max_ending_here + a[i]
        if (max_so_far < max_ending_here)
            max_so_far = max_ending_here
 
        if (max_ending_here < 0)
            max_ending_here = 0
    }
    return max_so_far
}
  
// Driver code
var a = [ -2, -3, 4, -1, -2, 1, 5, -3 ]
document.write("Maximum contiguous sum is",
               maxSubArraySum(a, a.length))
  
// This code is contributed by AnkThon
 
</script>

Producción:

Maximum contiguous sum is 7

Otro enfoque:

<script>
        // JavaScript Program to implement
        // the above approach
 
        function maxSubarraySum(arr, size)
        {
            let max_ending_here = 0, max_so_far = Number.MIN_VALUE;
            for (let i = 0; i < size; i++) {
 
                // include current element to previous subarray only
                // when it can add to a bigger number than itself.
                if (arr[i] <= max_ending_here + arr[i]) {
                    max_ending_here += arr[i];
                }
 
                // Else start the max subarray from current element
                else {
                    max_ending_here = arr[i];
                }
                if (max_ending_here > max_so_far) {
                    max_so_far = max_ending_here;
                }
            }
            return max_so_far;
        }
         
// This code is contributed by Potta Lokesh
    </script>

Complejidad del tiempo: O(n) 
Paradigma algorítmico: Programación dinámica
A continuación se muestra otra implementación sencilla sugerida por Mohit Kumar . La implementación maneja el caso cuando todos los números en la array son negativos. 

<script>
// C# program to print largest
// contiguous array sum
 
function maxSubArraySum(a,size)
{
  let max_so_far = a[0];
  let curr_max = a[0];
 
  for (let i = 1; i < size; i++)
  {
      curr_max = Math.max(a[i], curr_max+a[i]);
      max_so_far = Math.max(max_so_far, curr_max);
  }
 
return max_so_far;
}
 
// Driver code
 
let a = [-2, -3, 4, -1, -2, 1, 5, -3];
let n = a.length;
document.write("Maximum contiguous sum is ",maxSubArraySum(a, n));
     
</script>

Producción: 

Maximum contiguous sum is 7

Para imprimir el subarreglo con la suma máxima, mantenemos índices siempre que obtengamos la suma máxima.  

<script>
// javascript program to print largest
// contiguous array sum   
function maxSubArraySum(a , size) {
        var max_so_far = Number.MIN_VALUE, max_ending_here = 0, start = 0, end = 0, s = 0;
 
        for (i = 0; i < size; i++) {
            max_ending_here += a[i];
 
            if (max_so_far < max_ending_here) {
                max_so_far = max_ending_here;
                start = s;
                end = i;
            }
 
            if (max_ending_here < 0) {
                max_ending_here = 0;
                s = i + 1;
            }
        }
        document.write("Maximum contiguous sum is " + max_so_far);
        document.write("<br/>Starting index " + start);
        document.write("<br/>Ending index " + end);
    }
 
    // Driver code
     
        var a = [ -2, -3, 4, -1, -2, 1, 5, -3 ];
        var n = a.length;
        maxSubArraySum(a, n);
 
// This code is contributed by Rajput-Ji
</script>

Producción: 

Maximum contiguous sum is 7
Starting index 2
Ending index 6

El algoritmo de Kadane se puede ver tanto como codicioso como como DP. Como podemos ver, mantenemos una suma continua de enteros y cuando se vuelve menor que 0, la restablecemos a 0 (parte codiciosa). Esto se debe a que continuar con una suma negativa es mucho peor que reiniciar con un nuevo rango. Ahora también se puede ver como un DP, en cada etapa tenemos 2 opciones: tomar el elemento actual y continuar con la suma anterior O reiniciar un nuevo rango. Estas dos opciones están siendo atendidas en la implementación. 

Complejidad de tiempo: O(n)

Espacio Auxiliar: O(1)

Ahora intente la siguiente pregunta 
Dada una array de enteros (posiblemente algunos elementos negativos), escriba un programa C para encontrar el *producto máximo* posible multiplicando ‘n’ enteros consecutivos en la array donde n ≤ ARRAY_SIZE. Además, imprima el punto de inicio del subarreglo de producto máximo.

Consulte el artículo completo sobre el subarreglo contiguo de suma más grande para obtener más detalles.