Dada una string binaria S , la tarea es escribir un programa para DFA Machine que acepte una string con números impares de 0 y 1 .
Ejemplos:
Entrada: S = “010011”
Salida: Aceptada
Explicación:
La string dada S contiene un número impar de ceros y unos.Entrada: S = “00000”
Salida: No aceptado
Explicación:
La string dada S no contiene un número impar de ceros y unos.
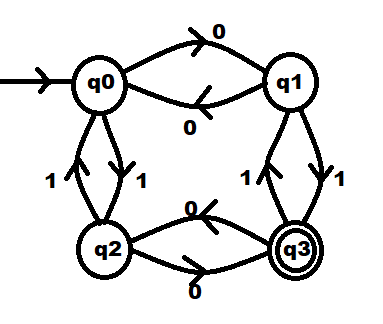
Enfoque: a continuación se muestra la máquina DFA diseñada para el problema dado. Construya una tabla de transición para los estados de DFA y analice las transiciones entre cada estado. A continuación se muestran los pasos:
- Hay 4 estados q 0 , q 1 , q 2 , q 3 donde q 0 es el estado inicial y q 3 es el estado final.
- La tabla de transición del DFA anterior es la siguiente:
| Estado actual | estado final | |
| 0 | 1 | |
| q 0 | q 1 | q 2 |
| q 1 | q 0 | q 3 |
| q 2 | q 3 | q 0 |
| q 3 | q 2 | q 1 |
- A través de esta tabla, entienda las transiciones en el DFA.
- Si se alcanza el estado final ( q 3 ) después de leer toda la string, entonces la string se acepta; de lo contrario, no se acepta.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to check whether the given
// string is accepted by DFA or not
void checkValidDFA(string s)
{
// Stores initial state of DFA
int initial_state = 0;
// Stores final state of DFA
int final_state;
// Stores previous state of DFA
int previous_state = 0;
// Iterate through the string
for (int i = 0; i < s.length(); i++) {
// Checking for all combinations
if ((s[i] == '0'
&& previous_state == 0)
|| (s[i] == '1'
&& previous_state == 3)) {
final_state = 1;
}
else if ((s[i] == '0'
&& previous_state == 3)
|| (s[i] == '1'
&& previous_state == 0)) {
final_state = 2;
}
else if ((s[i] == '0'
&& previous_state == 1)
|| (s[i] == '1'
&& previous_state == 2)) {
final_state = 0;
}
else if ((s[i] == '0'
&& previous_state == 2)
|| (s[i] == '1'
&& previous_state == 1)) {
final_state = 3;
}
// Update the previous_state
previous_state = final_state;
}
// If final state is reached
if (final_state == 3) {
cout << "Accepted" << endl;
}
// Otherwise
else {
cout << "Not Accepted" << endl;
}
}
// Driver Code
int main()
{
// Given string
string s = "010011";
// Function Call
checkValidDFA(s);
return 0;
}
Python3
# Python3 program for the above approach
# Function to check whether the given
# is accepted by DFA or not
def checkValidDFA(s):
# Stores initial state of DFA
initial_state = 0
# Stores final state of DFA
final_state = 0
# Stores previous state of DFA
previous_state = 0
# Iterate through the string
for i in range(len(s)):
# Checking for all combinations
if ((s[i] == '0' and previous_state == 0) or
(s[i] == '1' and previous_state == 3)):
final_state = 1
elif ((s[i] == '0' and previous_state == 3) or
(s[i] == '1' and previous_state == 0)):
final_state = 2
elif ((s[i] == '0' and previous_state == 1) or
(s[i] == '1' and previous_state == 2)):
final_state = 0
elif ((s[i] == '0' and previous_state == 2) or
(s[i] == '1' and previous_state == 1)):
final_state = 3
# Update the previous_state
previous_state = final_state
# If final state is reached
if (final_state == 3):
print("Accepted")
# Otherwise
else:
print("Not Accepted")
# Driver Code
if __name__ == '__main__':
# Given string
s = "010011"
# Function Call
checkValidDFA(s)
# This code is contributed by mohit kumar 29
Java
// Java program for the above approach
import java.util.*;
class GFG{
// Function to check whether the given
// string is accepted by DFA or not
static void checkValidDFA(String s)
{
// Stores initial state of DFA
int initial_state = 0;
// Stores final state of DFA
int final_state = 0;
// Stores previous state of DFA
int previous_state = 0;
// Iterate through the string
for(int i = 0; i < s.length(); i++)
{
// Checking for all combinations
if ((s.charAt(i) == '0' && previous_state == 0) ||
(s.charAt(i) == '1' && previous_state == 3))
{
final_state = 1;
}
else if ((s.charAt(i) == '0' && previous_state == 3) ||
(s.charAt(i) == '1' && previous_state == 0))
{
final_state = 2;
}
else if ((s.charAt(i) == '0' && previous_state == 1) ||
(s.charAt(i) == '1' && previous_state == 2))
{
final_state = 0;
}
else if ((s.charAt(i) == '0' && previous_state == 2) ||
(s.charAt(i) == '1' && previous_state == 1))
{
final_state = 3;
}
// Update the previous_state
previous_state = final_state;
}
// If final state is reached
if (final_state == 3)
{
System.out.println("Accepted");
}
// Otherwise
else
{
System.out.println("Not Accepted");
}
}
// Driver Code
public static void main(String args[])
{
// Given string
String s = "010011";
// Function Call
checkValidDFA(s);
}
}
// This code is contributed by bgangwar59
C#
// C# program for the above approach
using System;
class GFG{
// Function to check whether the given
// string is accepted by DFA or not
static void checkValidDFA(string s)
{
// Stores initial state of DFA
//int initial_state = 0;
// Stores final state of DFA
int final_state = 0;
// Stores previous state of DFA
int previous_state = 0;
// Iterate through the string
for(int i = 0; i < s.Length; i++)
{
// Checking for all combinations
if ((s[i] == '0' && previous_state == 0) ||
(s[i] == '1' && previous_state == 3))
{
final_state = 1;
}
else if ((s[i] == '0' && previous_state == 3) ||
(s[i] == '1' && previous_state == 0))
{
final_state = 2;
}
else if ((s[i] == '0' && previous_state == 1) ||
(s[i] == '1' && previous_state == 2))
{
final_state = 0;
}
else if ((s[i] == '0' && previous_state == 2) ||
(s[i] == '1' && previous_state == 1))
{
final_state = 3;
}
// Update the previous_state
previous_state = final_state;
}
// If final state is reached
if (final_state == 3)
{
Console.WriteLine("Accepted");
}
// Otherwise
else
{
Console.WriteLine("Not Accepted");
}
}
// Driver Code
public static void Main()
{
// Given string
string s = "010011";
// Function Call
checkValidDFA(s);
}
}
// This code is contributed by sanjoy_62
Javascript
<script>
// JavaScript program for the above approach
// Function to check whether the given
// string is accepted by DFA or not
function checkValidDFA(s) {
// Stores initial state of DFA
// int initial_state = 0;
// Stores final state of DFA
var final_state = 0;
// Stores previous state of DFA
var previous_state = 0;
// Iterate through the string
for (var i = 0; i < s.length; i++) {
// Checking for all combinations
if (
(s[i] === "0" && previous_state === 0) ||
(s[i] === "1" && previous_state === 3)
) {
final_state = 1;
} else if (
(s[i] === "0" && previous_state === 3) ||
(s[i] === "1" && previous_state === 0)
) {
final_state = 2;
} else if (
(s[i] === "0" && previous_state === 1) ||
(s[i] === "1" && previous_state === 2)
) {
final_state = 0;
} else if (
(s[i] === "0" && previous_state === 2) ||
(s[i] === "1" && previous_state === 1)
) {
final_state = 3;
}
// Update the previous_state
previous_state = final_state;
}
// If final state is reached
if (final_state === 3) {
document.write("Accepted");
}
// Otherwise
else {
document.write("Not Accepted");
}
}
// Driver Code
// Given string
var s = "010011";
// Function Call
checkValidDFA(s);
</script>
Accepted
Complejidad temporal: O(N)
Espacio auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por pravallika26 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA