Dada una función f(x) sobre el número flotante x y dos números ‘a’ y ‘b’ tales que f(a)*f(b) < 0 y f(x) es continua en [a, b]. Aquí f(x) representa una ecuación algebraica o trascendental. Encuentre la raíz de la función en el intervalo [a, b] (O encuentre un valor de x tal que f(x) sea 0).
Input: A function of x, for example x3 – x2 + 2.
And two values: a = -200 and b = 300 such that
f(a)*f(b) < 0, i.e., f(a) and f(b) have
opposite signs.
Output: The value of root is : -1.00
OR any other value close to root.
Recomendamos encarecidamente consultar la publicación a continuación como un requisito previo de esta publicación.
Solución de Ecuaciones Algebraicas y Trascendentales | Conjunto 1 (El método de bisección)
En esta publicación se analiza el método de la posición falsa. Este método también se conoce como Regula Falsi o El Método de los Acordes.
Similitudes con el método de bisección:
- Mismas Suposiciones: Este método también asume que la función es continua en [a, b] y dados dos números ‘a’ y ‘b’ son tales que f(a) * f(b) < 0.
- Siempre converge: al igual que la bisección, siempre converge, generalmente considerablemente más rápido que la bisección, pero a veces mucho más lentamente que la bisección.
Diferencias con el Método de Bisección:
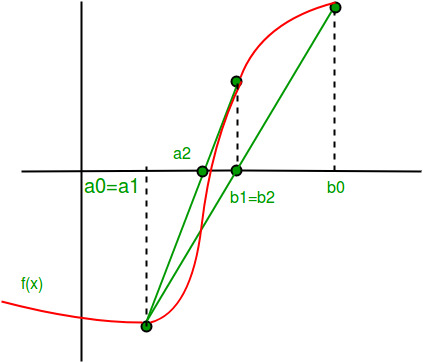
Se diferencia en que hacemos una cuerda uniendo los dos puntos [a, f(a)] y [b, f(b)]. Consideramos el punto en el que la cuerda toca el eje x y lo llamamos c.
Pasos:
- Escribe la ecuación de la recta que une los dos puntos.
y – f(a) = ( (f(b)-f(a))/(b-a) )*(x-a) Now we have to find the point which touches x axis. For that we put y = 0. so x = a - (f(a)/(f(b)-f(a))) * (b-a) x = (a*f(b) - b*f(a)) / (f(b)-f(a)) This will be our c that is c = x.
- Si f(c) == 0, entonces c es la raíz de la solución.
- De lo contrario f(c) != 0
- Si el valor f(a)*f(c) < 0 entonces la raíz se encuentra entre a y c. Entonces recurrimos para a y c
- De lo contrario, si f(b)*f(c) < 0, entonces la raíz se encuentra entre b y c. Entonces recurrimos b y c.
- De lo contrario , la función dada no sigue una de las suposiciones.
Dado que la raíz puede ser un número de punto flotante y puede converger muy lentamente en el peor de los casos, iteramos una gran cantidad de veces para que la respuesta se acerque más a la raíz.
A continuación se muestra la implementación.
C++
// C++ program for implementation of Bisection Method for
// solving equations
#include<bits/stdc++.h>
using namespace std;
#define MAX_ITER 1000000
// An example function whose solution is determined using
// Bisection Method. The function is x^3 - x^2 + 2
double func(double x)
{
return x*x*x - x*x + 2;
}
// Prints root of func(x) in interval [a, b]
void regulaFalsi(double a, double b)
{
if (func(a) * func(b) >= 0)
{
cout << "You have not assumed right a and b\n";
return;
}
double c = a; // Initialize result
for (int i=0; i < MAX_ITER; i++)
{
// Find the point that touches x axis
c = (a*func(b) - b*func(a))/ (func(b) - func(a));
// Check if the above found point is root
if (func(c)==0)
break;
// Decide the side to repeat the steps
else if (func(c)*func(a) < 0)
b = c;
else
a = c;
}
cout << "The value of root is : " << c;
}
// Driver program to test above function
int main()
{
// Initial values assumed
double a =-200, b = 300;
regulaFalsi(a, b);
return 0;
}
Java
// java program for implementation
// of Bisection Method for
// solving equations
import java.io.*;
class GFG {
static int MAX_ITER = 1000000;
// An example function whose
// solution is determined using
// Bisection Method. The function
// is x^3 - x^2 + 2
static double func(double x)
{
return (x * x * x - x * x + 2);
}
// Prints root of func(x)
// in interval [a, b]
static void regulaFalsi(double a, double b)
{
if (func(a) * func(b) >= 0)
{
System.out.println("You have not assumed right a and b");
}
// Initialize result
double c = a;
for (int i = 0; i < MAX_ITER; i++)
{
// Find the point that touches x axis
c = (a * func(b) - b * func(a))
/ (func(b) - func(a));
// Check if the above found point is root
if (func(c) == 0)
break;
// Decide the side to repeat the steps
else if (func(c) * func(a) < 0)
b = c;
else
a = c;
}
System.out.println("The value of root is : " + (int)c);
}
// Driver program
public static void main(String[] args)
{
// Initial values assumed
double a = -200, b = 300;
regulaFalsi(a, b);
}
}
// This article is contributed by vt_m
Python3
# Python3 implementation of Bisection
# Method for solving equations
MAX_ITER = 1000000
# An example function whose solution
# is determined using Bisection Method.
# The function is x^3 - x^2 + 2
def func( x ):
return (x * x * x - x * x + 2)
# Prints root of func(x) in interval [a, b]
def regulaFalsi( a , b):
if func(a) * func(b) >= 0:
print("You have not assumed right a and b")
return -1
c = a # Initialize result
for i in range(MAX_ITER):
# Find the point that touches x axis
c = (a * func(b) - b * func(a))/ (func(b) - func(a))
# Check if the above found point is root
if func(c) == 0:
break
# Decide the side to repeat the steps
elif func(c) * func(a) < 0:
b = c
else:
a = c
print("The value of root is : " , '%.4f' %c)
# Driver code to test above function
# Initial values assumed
a =-200
b = 300
regulaFalsi(a, b)
# This code is contributed by "Sharad_Bhardwaj".
C#
// C# program for implementation
// of Bisection Method for
// solving equations
using System;
class GFG {
static int MAX_ITER = 1000000;
// An example function whose
// solution is determined using
// Bisection Method. The function
// is x^3 - x^2 + 2
static double func(double x)
{
return (x * x * x - x * x + 2);
}
// Prints root of func(x)
// in interval [a, b]
static void regulaFalsi(double a, double b)
{
if (func(a) * func(b) >= 0)
{
Console.WriteLine("You have not assumed right a and b");
}
// Initialize result
double c = a;
for (int i = 0; i < MAX_ITER; i++)
{
// Find the point that touches x axis
c = (a * func(b) - b * func(a))
/ (func(b) - func(a));
// Check if the above found point is root
if (func(c) == 0)
break;
// Decide the side to repeat the steps
else if (func(c) * func(a) < 0)
b = c;
else
a = c;
}
Console.WriteLine("The value of root is : " + (int)c);
}
// Driver program
public static void Main(String []args)
{
// Initial values assumed
double a = -200, b = 300;
regulaFalsi(a, b);
}
}
// This code is contributed by Sam007.
Javascript
<script>
// JavaScript program for implementation of Bisection Method for
// solving equations
let MAX_ITER = 1000000
// An example function whose solution is determined using
// Bisection Method. The function is x^3 - x^2 + 2
function func(x){
return x*x*x - x*x + 2;
}
// Prints root of func(x) in interval [a, b]
function regulaFalsi( a, b){
if (func(a) * func(b) >= 0){
document.write("You have not assumed right a and b\n");
return;
}
// Initialize result
let c = a;
for (let i=0; i < MAX_ITER; i++)
{
// Find the point that touches x axis
c = Math.floor((a*func(b) - b*func(a))/ (func(b) - func(a)));
// Check if the above found point is root
if (func(c)==0){
break;
}
// Decide the side to repeat the steps
else if (func(c)*func(a) < 0){
b = c;
}
else{
a = c;
}
}
document.write("The value of root is : " + c);
}
// Driver program to test above function
// Initial values assumed
let a =-200;
let b = 300;
regulaFalsi(a, b);
</script>
Producción:
The value of root is : -1
Este método siempre converge, por lo general considerablemente más rápido que la bisección. Pero el peor de los casos puede ser muy lento.
Pronto discutiremos otros métodos para resolver ecuaciones algebraicas y trascendentales.
Referencias:
Métodos introductorios de análisis numérico por SS Sastry
https://en.wikipedia.org/wiki/False_position_method
Este artículo es una contribución de Abhiraj Smit . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA