Dado el triángulo inscrito en un polígono regular de N lados con una longitud de lado dada, formado usando 3 vértices cualesquiera del polígono, la tarea es encontrar el área de este triángulo.
Ejemplos:
Input: N = 6, side = 10 Output: 129.904 Input: N = 8, side = 5 Output: 45.2665
Enfoque: Considere el primer ejemplo:
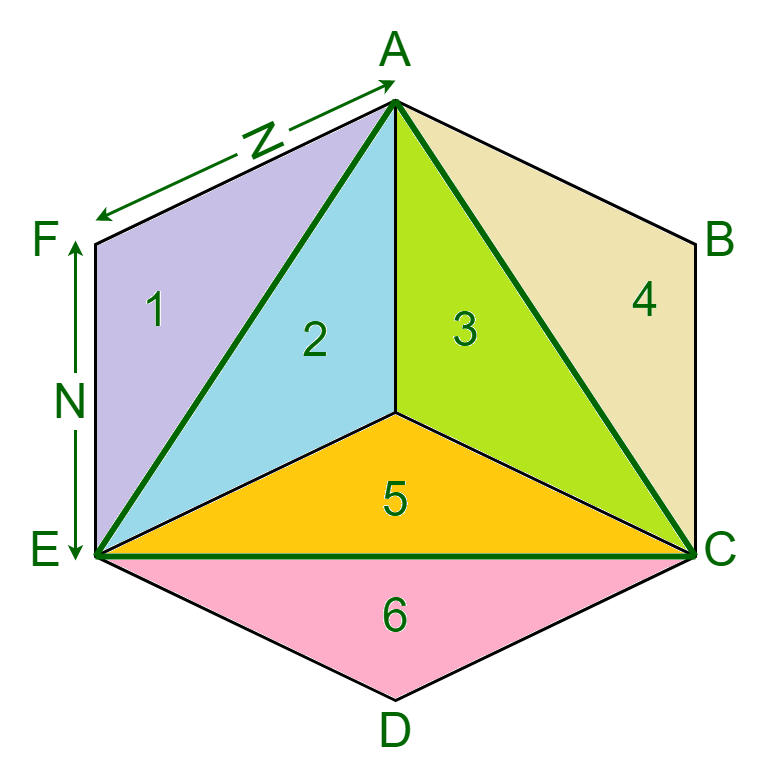
- Se muestra un polígono regular ABCDEF de 6 lados con un triángulo AEC inscrito en él.
- Como puede verse, el triángulo divide el polígono dado en 6 áreas triangulares iguales, donde el punto de intersección del triángulo AEC es el baricentro del triángulo.
- Encuentra el área del polígono regular. El área del polígono regular se puede calcular con la ayuda de la fórmula (A*P)/2 donde P es el perímetro de ese polígono y A es la apotema de ese polígono .
- El área de cada una de las partes trianguladas será (Área Triangulada = Área del polígono regular de N lados / N) de la ley de simetría.
- Dado que el triángulo ACE se compone de 3 de 6, el área del triángulo ACE será (3 * área triangulada)
- Por lo tanto, en general, si existe un polígono regular de N lados con área A, el área de un triángulo inscrito en él será (A/N)*3 .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ Program to find the area of a triangle
// inscribed in N-sided regular polygon
#include <bits/stdc++.h>
#include <cmath>
using namespace std;
// Function to find the area of the polygon
double area_of_regular_polygon(double n, double len)
{
// area of a regular polygon with N sides
// and side length len
double P = (len * n);
double A
= len
/ (2 * tan((180 / n)
* 3.14159 / 180));
double area = (P * A) / 2;
return area;
}
// Function to find the area of a triangle
double area_of_triangle_inscribed(double n, double len)
{
double area = area_of_regular_polygon(n, len);
// area of one triangle
// in an N-sided regular polygon
double triangle = area / n;
// area of inscribed triangle
double ins_tri = (triangle * 3);
return ins_tri;
}
// Driver code
int main()
{
double n = 6, len = 10;
cout << area_of_triangle_inscribed(n, len)
<< endl;
return 0;
}
Java
// Java Program to find the area of a triangle
// inscribed in N-sided regular polygon
import java.util.*;
class GFG
{
// Function to find the area of the polygon
static double area_of_regular_polygon(double n,
double len)
{
// area of a regular polygon with N sides
// and side length len
double P = (len * n);
double A = len / (2 * Math.tan((180 / n) *
3.14159 / 180));
double area = (P * A) / 2;
return area;
}
// Function to find the area of a triangle
static double area_of_triangle_inscribed(double n,
double len)
{
double area = area_of_regular_polygon(n, len);
// area of one triangle
// in an N-sided regular polygon
double triangle = area / n;
// area of inscribed triangle
double ins_tri = (triangle * 3);
return ins_tri;
}
// Driver code
static public void main(String[] arg)
{
double n = 6, len = 10;
System.out.printf("%.3f",
area_of_triangle_inscribed(n, len));
}
}
// This code is contributed by PrinciRaj1992
Python3
# Python3 Program to find the area # of a triangle inscribed in # N-sided regular polygon import math # Function to find the area of the polygon def area_of_regular_polygon(n, len): # area of a regular polygon with # N sides and side length len P = (len * n); A = len / (2 * math.tan((180 / n) * 3.14159 / 180)) area = (P * A) / 2 return area # Function to find the area of a triangle def area_of_triangle_inscribed(n, len): area = area_of_regular_polygon(n, len) # area of one triangle # in an N-sided regular polygon triangle = area / n # area of inscribed triangle ins_tri = (triangle * 3); return ins_tri # Driver code n = 6 len = 10 print(round(area_of_triangle_inscribed(n, len), 3)) # This code is contributed by divyamohan
C#
// C# Program to find the area of a triangle
// inscribed in N-sided regular polygon
using System;
class GFG
{
// Function to find the area of the polygon
static double area_of_regular_polygon(double n,
double len)
{
// area of a regular polygon with N sides
// and side length len
double P = (len * n);
double A = len / (2 * Math.Tan((180 / n) *
3.14159 / 180));
double area = (P * A) / 2;
return area;
}
// Function to find the area of a triangle
static double area_of_triangle_inscribed(double n,
double len)
{
double area = area_of_regular_polygon(n, len);
// area of one triangle
// in an N-sided regular polygon
double triangle = area / n;
// area of inscribed triangle
double ins_tri = (triangle * 3);
return ins_tri;
}
// Driver code
static public void Main(String[] arg)
{
double n = 6, len = 10;
Console.Write("{0:F3}",
area_of_triangle_inscribed(n, len));
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// javascript Program to find the area of a triangle
// inscribed in N-sided regular polygon
// Function to find the area of the polygon
function area_of_regular_polygon(n, len)
{
// area of a regular polygon with N sides
// and side length len
let P = (len * n);
let A
= len
/ (2 * Math.tan((180 / n)
* 3.14159 / 180));
let area = (P * A) / 2;
return area;
}
// Function to find the area of a triangle
function area_of_triangle_inscribed( n, len)
{
let area = area_of_regular_polygon(n, len);
// area of one triangle
// in an N-sided regular polygon
let triangle = area / n;
// area of inscribed triangle
let ins_tri = (triangle * 3);
return ins_tri;
}
// Driver code
let n = 6, len = 10;
document.write( area_of_triangle_inscribed(n, len).toFixed(3));
// This code is contributed by todaysgaurav
</script>
Producción:
129.904
Complejidad de tiempo: O(1), el código se ejecutará en un tiempo constante.
Espacio auxiliar: O(1), no se requiere espacio adicional, por lo que es una constante.
Publicación traducida automáticamente
Artículo escrito por charlie_04 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA