Programa para encontrar la suma de la secuencia dada

Dados dos números $N$ y $K$ . La tarea es encontrar la suma de la secuencia dada a continuación.

(1*2*3*…*k) + (2*3*…*k*(k+1)) + (3*4*..*(k+1)*(k+2)) +… ..+((n-k+1)*(n-k+2)*…*(n-k+k)).

Dado que la salida puede ser grande, imprima la respuesta en el módulo 10^9+7.
Ejemplos :

Input : N = 3, K = 2
Output : 8

Input : N = 4, K = 2
Output : 20

Tomemos el ejemplo dado e intentemos reducirlo a una fórmula general.
En el ejemplo dado para n = 3 y k=2 ,

Sum = 1*2 + 2*3

Sabemos que:
$$1\times2=2!\times 0!$\\ $2\times3=3!\times1!$\\$
Entonces cada término es de la forma:

$\frac{x!}{\left(x-k\right)!}$

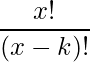
Si multiplicamos y dividimos por $k!$ , se convierte en

$k!\cdot\frac{x!}{\left(x-k\right)!\cdot k!}$

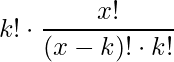
Lo cual no es más que,
$$k!\times$${N}\choose{k}$\\$
Por lo tanto,
$sum = $k\times \sum_{x=k}^{n}$${x}\choose{k}$=${n+1}\choose{k+1}$$\times k! $\\$
Pero como n es tan grande que no podemos calcularlo directamente, tenemos que simplificar la expresión anterior.
Al simplificar obtenemos,

$\frac{\left(n\right) \cdot \left(n-1\right) \cdot \left(n-2\right) \dots \left(n-k+1\right)}{k+1}$

A continuación se muestra la implementación de la idea anterior:

C++

// CPP program to find the sum of the
// given sequence
 
#include <bits/stdc++.h>
using namespace std;
 
const long long MOD = 1000000007;
 
// function to find modulo inverse
// under 10^9+7
long long modInv(long long x)
{
    long long n = MOD - 2;
    long long result = 1;
    while (n) {
        if (n & 1)
            result = result * x % MOD;
        x = x * x % MOD;
        n = n / 2;
    }
     
    return result;
}
 
// Function to find the sum of the
// given sequence
long long getSum(long long n, long long k)
{
    long long ans = 1;
     
    for (long long i = n + 1; i > n - k; i--)
        ans = ans * i % MOD;
    ans = ans * modInv(k + 1) % MOD;
     
    return ans;
}
 
// Driver code
int main()
{
    long long n = 3, k = 2;
     
    cout<<getSum(n,k);
     
    return 0;
}

Java

// Java program to find the sum of the
// given sequence
 
class GFG {
 
    static long MOD = 1000000007;
 
// function to find modulo inverse
// under 10^9+7
    static long modInv(long x) {
        long n = MOD - 2;
        long result = 1;
        while (n > 0) {
            if ((n & 1) > 0) {
                result = result * x % MOD;
            }
            x = x * x % MOD;
            n = n / 2;
        }
 
        return result;
    }
 
// Function to find the sum of the
// given sequence
    static long getSum(long n, long k) {
        long ans = 1;
 
        for (long i = n + 1; i > n - k; i--) {
            ans = ans * i % MOD;
        }
        ans = ans * modInv(k + 1) % MOD;
 
        return ans;
    }
 
// Driver code
    public static void main(String[] args) {
        long n = 3, k = 2;
        System.out.println(getSum(n, k));
    }
}

Python3

# Python3 program to find the sum
# of the given sequence
 
MOD = 1000000007;
 
# function to find modulo inverse
# under 10^9+7
def modInv(x):
 
    n = MOD - 2;
    result = 1;
    while (n):
        if (n&1):
            result = result * x % MOD;
        x = x * x % MOD;
        n = int(n / 2);
     
    return result;
 
# Function to find the sum of
# the given sequence
def getSum(n, k):
 
    ans = 1;
     
    for i in range(n + 1, n - k, -1):
        ans = ans * i % MOD;
    ans = ans * modInv(k + 1) % MOD;
     
    return ans;
 
# Driver code
n = 3;
k = 2;
     
print(getSum(n,k));
     
# This code is contributed by mits

C#

// C# program to find the sum of the
// given sequence
using System;
 
  
 
// function to find modulo inverse
// under 10^9+7
class gfg
{
    public long MOD = 1000000007;
 public long modInv(long x)
 {
    long n = MOD - 2;
    long result = 1;
    while (n >0) {
        if ((n & 1) > 0)
            result = result * x % MOD;
        x = x * x % MOD;
        n = n / 2;
    }
     
    return result;
}
 
// Function to find the sum of the
// given sequence
  public long getSum(long n, long k)
  {
    long ans = 1;
     
    for (long i = n + 1; i > n - k; i--)
        ans = ans * i % MOD;
    ans = ans * modInv(k + 1) % MOD;
     
    return ans;
 }
}
 
// Driver code
class geek
{
  public static int Main()
 {
     gfg g = new gfg();
    long n = 3, k = 2;
     
    Console.WriteLine(g.getSum(n,k));
     
    return 0;
 }
}
//This code is contributed by SoumikMondal

PHP

<?php
// PHP program to find the sum of
// the given sequence
 
// function to find modulo inverse
// under 10^9+7
function modInv($x)
{
    $MOD = 1000000007;
    $n = $MOD - 2;
    $result = 1;
    while ($n)
    {
        if ($n & 1)
            $result = $result * $x % $MOD;
        $x = $x * $x % $MOD;
        $n = $n / 2;
    }
     
    return $result;
}
 
// Function to find the sum of the
// given sequence
function getSum($n, $k)
{
    $MOD = 1000000007;
    $ans = 1;
     
    for ($i = $n + 1; $i > $n - $k; $i--)
        $ans = $ans * $i % $MOD;
    $ans = $ans * modInv($k + 1) % $MOD;
     
    return $ans;
}
 
// Driver code
$n = 3; $k = 2;
     
echo getSum($n, $k);
 
// This code is contributed
// by Akanksha Rai
?>

Javascript

<script>
 
// Javascript program to find the sum of the
// given sequence
 
var MOD = 100000007;
 
// function to find modulo inverse
// under 10^9+7
function modInv(x)
{
    var n = MOD - 2;
    var result = 1;
    while (n) {
        if (n & 1)
            result = result * x % MOD;
        x = x * x % MOD;
        n = n / 2;
    }
     
    return result;
}
 
// Function to find the sum of the
// given sequence
function getSum(n, k)
{
    var ans = 1;
     
    for (var i = n + 1; i > n - k; i--)
        ans = ans * i % MOD;
    ans = ans * modInv(k + 1) % MOD;
     
    return ans;
}
 
// Driver code
var n = 3, k = 2;
 
document.write( getSum(n,k));
 
// This code is contributed by noob2000.
</script>

Producción

Complejidad temporal: O(k+log(m)) donde k es el número dado ym es el valor del módulo.
Espacio Auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por sahilshelangia y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

PHP

Javascript

Deja una respuesta Cancelar la respuesta