Programa para números de Perrin

Posted on by Rudeus Greyrat

Los números de Perrin son los números en la siguiente secuencia de enteros. 
3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39… 
En términos matemáticos, la secuencia p(n) de los números de Perrin está definida por la relación de recurrencia 
 

 P(n) = P(n-2) + P(n-3) for n > 2, 

with initial values
    P(0) = 3, P(1) = 0, P(2) = 2.

Escriba una función int per(int n) que devuelva p(n). Por ejemplo, si n = 0, entonces per() debería devolver 3. Si n = 1, entonces debería devolver 0 Si n = 2, entonces debería devolver 2. Para n > 2, debería devolver p(n-2 ) + p(n-3) 
 

Método 1 (Usar recursividad: Exponencial) 
A continuación se muestra una implementación recursiva simple de la fórmula anterior.
 

C++

// n'th perrin number using Recursion'
#include <bits/stdc++.h>
using namespace std;
 
int per(int n)
{
    if (n == 0)
        return 3;
    if (n == 1)
        return 0;
    if (n == 2)
        return 2;
    return per(n - 2) + per(n - 3);
}
 
// Driver code
int main()
{
    int n = 9;
    cout << per(n);
    return 0;
}
 
// This code is contributed
// by Akanksha Rai

C

// n'th perrin number using Recursion'
#include <stdio.h>
int per(int n)
{
    if (n == 0)
        return 3;
    if (n == 1)
        return 0;
    if (n == 2)
        return 2;
    return per(n - 2) + per(n - 3);
}
 
// Driver code
int main()
{
    int n = 9;
    printf("%d", per(n));
    return 0;
}

Java

// Java code for n'th perrin number
// using Recursion'
import java.io.*;
 
class GFG {
 
    static int per(int n)
    {
        if (n == 0)
            return 3;
        if (n == 1)
            return 0;
        if (n == 2)
            return 2;
        return per(n - 2) + per(n - 3);
    }
 
    // Driver code
    public static void main(String[] args)
    {
 
        int n = 9;
 
        System.out.println(per(n));
    }
}
 
// This code is contributed by vt_m.

Python3

# Python3 code for n'th perrin
# number using Recursion'
 
# function return n'th
# perrin number
def per(n):
 
    if (n == 0):
        return 3;
    if (n == 1):
        return 0;
    if (n == 2):
        return 2;
    return per(n - 2) + per(n - 3);
 
# Driver Code
n = 9;
print(per(n));
     
# This code is contributed mits

C#

// C# code for n'th perrin number
// using Recursion'
using System;
 
class GFG {
 
    static int per(int n)
    {
        if (n == 0)
            return 3;
        if (n == 1)
            return 0;
        if (n == 2)
            return 2;
        return per(n - 2) + per(n - 3);
    }
 
    // Driver code
    public static void Main()
    {
 
        int n = 9;
 
        Console.Write(per(n));
    }
}
 
// This code is contributed by vt_m.

PHP

<?php
// PHP code for n'th perrin
// number using Recursion'
 
// function return n'th
// perrin number
function per($n)
{
    if ($n == 0)
        return 3;
    if ($n == 1)
        return 0;
    if ($n == 2)
        return 2;
    return per($n - 2) +
           per($n - 3);
}
 
    // Driver Code
    $n = 9;
    echo per($n);
     
#This code is contributed ajit.
?>

Javascript

<script>
 
// Javascript code for n'th perrin number
// using Recursion'
 
    function per(n)
    {
        if (n == 0)
            return 3;
        if (n == 1)
            return 0;
        if (n == 2)
            return 2;
        return per(n - 2) + per(n - 3);
    }
      
// Driver code   
 
           let n = 9;
   
        document.write(per(n));
         
</script>

Producción: 

12

Vemos que en esta implementación hay mucho trabajo repetido en el siguiente árbol de recursión. 
 

                           per(8)   
                       /           \     
               per(6)             per(5)   
              /      \             /     \
        per(4)      per(3)        per(3)    per(2)
       /     \        /    \        /  \  
   per(2)   per(1)  per(1) per(0) per(1) per(0)

Método 2: ( Optimizado : Lineal) 
 

C++

// Optimized C++ program for n'th perrin number
#include <bits/stdc++.h>
using namespace std;
int per(int n)
{
    int a = 3, b = 0, c = 2, i;
    int m;
    if (n == 0)
        return a;
    if (n == 1)
        return b;
    if (n == 2)
        return c;
    while (n > 2) {
        m = a + b;
        a = b;
        b = c;
        c = m;
        n--;
    }
    return m;
}
 
// Driver code
int main()
{
    int n = 9;
    cout << per(n);
    return 0;
}
 
// This code is contributed
// by Akanksha Rai

C

// Optimized C program for n'th perrin number
#include <stdio.h>
int per(int n)
{
    int a = 3, b = 0, c = 2, i;
    int m;
    if (n == 0)
        return a;
    if (n == 1)
        return b;
    if (n == 2)
        return c;
    while (n > 2) {
        m = a + b;
        a = b;
        b = c;
        c = m;
        n--;
    }
    return m;
}
 
// Driver code
int main()
{
    int n = 9;
    printf("%d", per(n));
    return 0;
}

Java

// Optimized Java program for n'th perrin number
import java.io.*;
 
class GFG {
 
    static int per(int n)
    {
        int a = 3, b = 0, c = 2, i;
        int m = 0;
        if (n == 0)
            return a;
        if (n == 1)
            return b;
        if (n == 2)
            return c;
        while (n > 2) {
            m = a + b;
            a = b;
            b = c;
            c = m;
            n--;
        }
        return m;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 9;
 
        System.out.println(per(n));
    }
}
 
// This code is contributed by vt_m.

Python3

# Optimized Python3 program for
# n'th perrin number
 
# function return the
# n'th perrin number
def per(n):
     
    a = 3;
    b = 0;
    c = 2;
 
    if (n == 0):
        return a;
    if (n == 1):
        return b;
    if (n == 2):
        return c;
    while (n > 2):
        m = a + b;
        a = b;
        b = c;
        c = m;
        n -= 1
     
    return m
 
# Driver code
n = 9;
print(per(n));
     
# This code is contributed by phasing17

C#

// Optimized C# program for n'th perrin number
using System;
 
class GFG {
 
    static int per(int n)
    {
        int a = 3, b = 0, c = 2;
 
        // int i;
        int m = 0;
        if (n == 0)
            return a;
        if (n == 1)
            return b;
        if (n == 2)
            return c;
 
        while (n > 2) {
            m = a + b;
            a = b;
            b = c;
            c = m;
            n--;
        }
 
        return m;
    }
 
    // Driver code
    public static void Main()
    {
 
        int n = 9;
 
        Console.WriteLine(per(n));
    }
}
 
// This code is contributed by vt_m.

PHP

<?php
// Optimized PHP program for
// n'th perrin number
 
// function return the
// n'th perrin number
function per($n)
{
    $a = 3; $b = 0;
    $c = 2; $i;
    $m;
    if ($n == 0)
        return $a;
    if ($n == 1)
        return $b;
    if ($n == 2)
        return $c;
    while ($n > 2)
    {
        $m = $a + $b;
        $a = $b;
        $b = $c;
        $c = $m;
        $n--;
    }
    return $m;
}
 
    // Driver code
    $n = 9;
    echo per($n);
     
// This code is contributed by ajit
?>

Javascript

<script>
// Optimized Javascript program for
// n'th perrin number
 
// function return the
// n'th perrin number
function per(n)
{
    let a = 3;
    let b = 0;
    let c = 2;
    let i;
    let m;
 
    if (n == 0)
        return a;
    if (n == 1)
        return b;
    if (n == 2)
        return c;
    while (n > 2)
    {
        m = a + b;
        a = b;
        b = c;
        c = m;
        n--;
    }
    return m;
}
 
    // Driver code
    n = 9;
    document.write(per(n));
     
// This code is contributed by _saurabh_jaiswal
</script>

Producción: 
 

12

Complejidad de tiempo: O(n) 
Espacio auxiliar: O(1)
Método 3: (Más optimizado: Logarítmico) 
Podemos optimizar aún más usando la Exponenciación matricial . La fórmula de potencia de la array para el n-ésimo número de Perrin es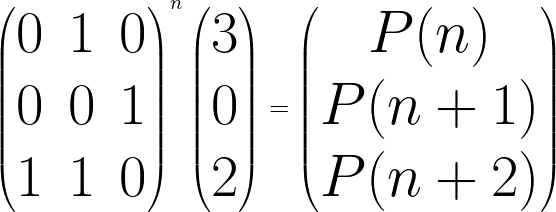 
{\Huge \begin{pmatrix} 0& 1 & 0\\ 0& 0&1 \\ 1 &1 & 0 \\ \end{pmatrix}^n \begin{pmatrix} 3\\ 0\\ 2 \end{pmatrix} = \begin{pmatrix} P(n)\\ P(n+1)\\ P(n+2) \end{pmatrix}}
Podemos implementar este método de manera similar a la implementación del método 5 de los números de Fibonacci . Dado que podemos calcular la n-ésima potencia de una array constante en O(Log n), la complejidad temporal de este método es O(Log n)
Aplicación: 
el número de conjuntos independientes máximos diferentes en un gráfico de ciclo de n vértices se cuenta mediante el n-ésimo número de Perrin para n > 1
Artículo relacionado:  
Suma de números de Perrin
Referencia: 
https://en.wikipedia.org/wiki/Perrin_number
Este artículo es una contribución de DANISH_RAZA . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
 

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *