Programa de Python para clasificación topológica

La ordenación topológica para el gráfico acíclico dirigido (DAG) es una ordenación lineal de vértices tal que para cada arista dirigida uv, el vértice u viene antes que v en la ordenación. La clasificación topológica de un gráfico no es posible si el gráfico no es un DAG.
Por ejemplo, una clasificación topológica del siguiente gráfico es «5 4 2 3 1 0». Puede haber más de una clasificación topológica para un gráfico. Por ejemplo, otra clasificación topológica del siguiente gráfico es «4 5 2 3 1 0». El primer vértice en la clasificación topológica es siempre un vértice con grado de entrada 0 (un vértice sin aristas entrantes).
 

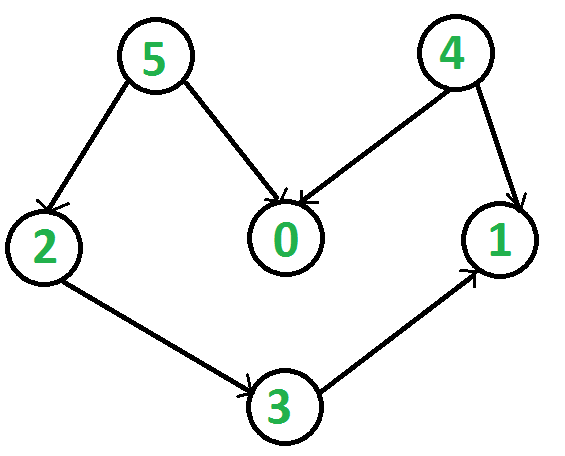
La clasificación topológica se puede implementar de forma recursiva y no recursiva. Primero, mostramos la versión recursiva más clara, luego proporcionamos el análisis de la versión no recursiva.
 

Clasificación topológica recursiva

#Python program to print topological sorting of a DAG
from collections import defaultdict
 
#Class to represent a graph
class Graph:
    def __init__(self,vertices):
        self.graph = defaultdict(list) #dictionary containing adjacency List
        self.V = vertices #No. of vertices
 
    # function to add an edge to graph
    def addEdge(self,u,v):
        self.graph[u].append(v)
 
    # A recursive function used by topologicalSort
    def topologicalSortUtil(self,v,visited,stack):
 
        # Mark the current node as visited.
        visited[v] = True
 
        # Recur for all the vertices adjacent to this vertex
        for i in self.graph[v]:
            if visited[i] == False:
                self.topologicalSortUtil(i,visited,stack)
 
        # Push current vertex to stack which stores result
        stack.insert(0,v)
 
    # The function to do Topological Sort. It uses recursive
    # topologicalSortUtil()
    def topologicalSort(self):
        # Mark all the vertices as not visited
        visited = [False]*self.V
        stack =[]
 
        # Call the recursive helper function to store Topological
        # Sort starting from all vertices one by one
        for i in range(self.V):
            if visited[i] == False:
                self.topologicalSortUtil(i,visited,stack)
 
        # Print contents of stack
        print (stack)
 
g= Graph(6)
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
 
print ("Following is a Topological Sort of the given graph")
g.topologicalSort()
#This code is contributed by Neelam Yadav

Producción: 

Following is a Topological Sort of the given graph
5 4 2 3 1 0

Clasificación topológica no recursiva

Algoritmo:

La forma en que se resuelve la clasificación topológica es procesando un Node después de que se hayan procesado todos sus hijos. Cada vez que se procesa un Node, se coloca en una pila para guardar el resultado final. Esta solución no recursiva se basa en el mismo concepto de DFS con un pequeño ajuste que se puede entender arriba y en este artículo . Sin embargo, a diferencia de la solución recursiva, que guarda el orden de los Nodes en la pila después de que todos los elementos vecinos se hayan colocado en la pila del programa, esta solución reemplaza la pila del programa con una pila de trabajo. Si un Node tiene un vecino que no ha sido visitado, el Node actual y el vecino se empujan a la pila de trabajo para ser procesados ​​hasta que no haya más vecinos disponibles para visitar.
Una vez que se han visitado todos los Nodes, lo que queda es el resultado final que se encuentra al imprimir el resultado de la pila al revés.

#Python program to print topological sorting of a DAG
from collections import defaultdict
 
#Class to represent a graph
class Graph:
    def __init__(self,vertices):
        self.graph = defaultdict(list) #dictionary containing adjacency List
        self.V = vertices #No. of vertices
 
    # function to add an edge to graph
    def addEdge(self,u,v):
        self.graph[u].append(v)
 
    # neighbors lazy generator given key
    def neighbor_gen(self,v):
        for k in self.graph[v]:
            yield k
     
    # non recursive topological sort
    def nonRecursiveTopologicalSortUtil(self, v, visited,stack):
         
        # working stack contains key and the corresponding current generator
        working_stack = [(v,self.neighbor_gen(v))]
         
        while len(working_stack) > 0:
            # get last element in stack
            v, gen = working_stack[-1]
            visited[v] = True
             
            # delete it from stack
            working_stack.pop()
             
            # run through neighbor generator until its empty
            continue_flag = True
            while continue_flag:
                next_neighbor = next(gen,None)
                 
                # if generator has returned all neighbors
                if next_neighbor is None:
                    continue_flag = False
                    # Save current key into the result stack
                    stack.append(v)
                    continue
                 
                # if new neighbor push current key and neighbor into stack
                if not(visited[next_neighbor]):
                    working_stack.append((v,gen))
                    working_stack.append((next_neighbor,self.neighbor_gen(next_neighbor)))
                    continue_flag = False
             
    # The function to do Topological Sort.
    def nonRecursiveTopologicalSort(self):
        # Mark all the vertices as not visited
        visited = [False]*self.V
         
        # result stack
        stack = []
 
        # Call the helper function to store Topological
        # Sort starting from all vertices one by one
        for i in range(self.V):
            if not(visited[i]):
                self.nonRecursiveTopologicalSortUtil(i, visited,stack)
         # Print contents of the stack in reverse
        print(stack[::-1])
 
g= Graph(6)
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
 
print("The following is a Topological Sort of the given graph")
g.nonRecursiveTopologicalSort()
# The following code was based of Neelam Yadav's code and is modified by Suhail Alnahari

Producción: 

Following is a Topological Sort of the given graph
5 4 2 3 1 0

Análisis de Complejidad:

• Complejidad de tiempo: O (V + E): el algoritmo anterior es simplemente DFS con una pila de trabajo y una pila de resultados. A diferencia de la solución recursiva, la profundidad de recursión no es un problema aquí.
• Espacio auxiliar: O(V): El espacio extra se necesita para las 2 pilas utilizadas.

Consulte el artículo completo sobre clasificación topológica para obtener más detalles.