Programa Python para imprimir todas las permutaciones de una string dada

Una permutación también llamada «número de arreglo» u «orden» es un reordenamiento de los elementos de una lista ordenada S en una correspondencia uno a uno con S mismo. ¡Una string de longitud n tiene n! permutación. 

Fuente: Mathword ( http://mathworld.wolfram.com/Permutation.html )

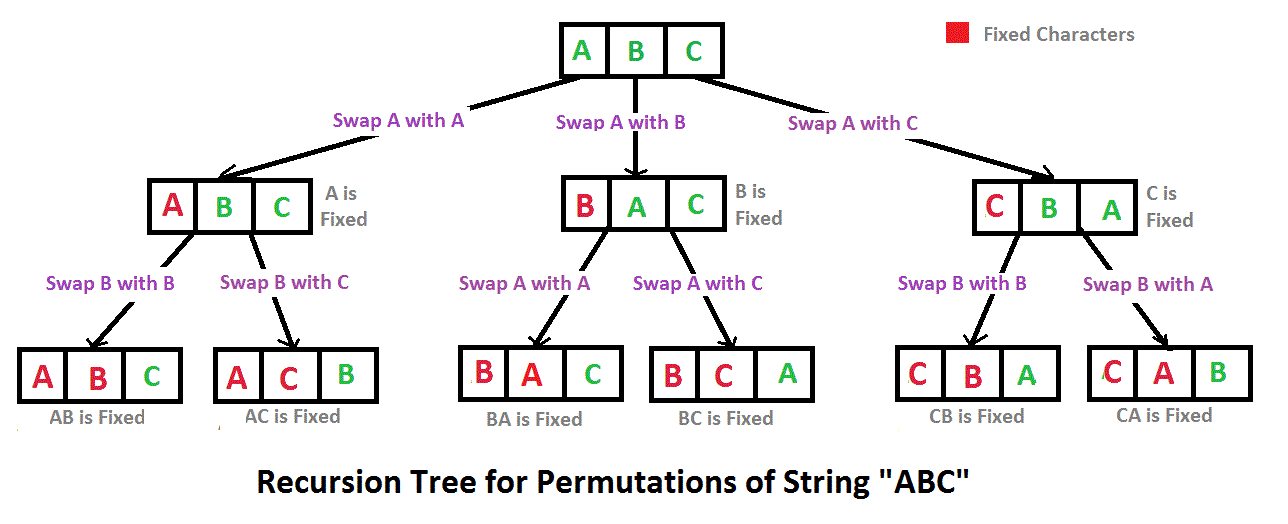
A continuación se muestran las permutaciones de la string ABC. 
ABC ACB BAC BCA CBA CABINA

Aquí hay una solución que se usa como base en el retroceso.

# Python program to print all permutations
# with duplicates allowed
def toString(List):
    return ''.join(List)
 
# Function to print permutations
# of string
# This function takes three parameters:
# 1. String
# 2. Starting index of the string
# 3. Ending index of the string.
def permute(a, l, r):
    if l == r:
        print (toString(a))
    else:
        for i in range(l, r + 1):
            a[l], a[i] = a[i], a[l]
            permute(a, l + 1, r)
 
            # backtrack
            a[l], a[i] = a[i], a[l]
 
# Driver code
string = "ABC"
n = len(string)
a = list(string)
permute(a, 0, n-1)
# This code is contributed by Bhavya Jain

Producción: 

ABC
ACB
BAC
BCA
CBA
CAB

Paradigma de algoritmo: retroceso 

Complejidad de tiempo: O(n*n!) Tenga en cuenta que hay n! permutaciones y requiere O(n) tiempo para imprimir una permutación.

Espacio Auxiliar: O(r – l)

Nota: La solución anterior imprime permutaciones duplicadas si hay caracteres repetidos en la string de entrada. Consulte el enlace a continuación para obtener una solución que imprima solo permutaciones distintas, incluso si hay duplicados en la entrada.
Imprime todas las permutaciones distintas de una string dada con duplicados.  
Permutaciones de una string dada usando STL

Otro enfoque:

# Python program to implement
# the above approach
def permute(s, answer):
    if (len(s) == 0):
        print(answer, end = "  ")
        return
     
    for i in range(len(s)):
        ch = s[i]
        left_substr = s[0:i]
        right_substr = s[i + 1:]
        rest = left_substr + right_substr
        permute(rest, answer + ch)
 
# Driver Code
answer = ""
s = input("Enter the string : ")
print("All possible strings are : ")
permute(s, answer)
# This code is contributed by Harshit Srivastava

Producción:

Enter the string : abc
All possible strings are : abc  acb  bac  bca  cab  cba

Complejidad de tiempo: O(n*n!) La complejidad de tiempo es la misma que en el enfoque anterior, es decir, ¡hay n! permutaciones y requiere O(n) tiempo para imprimir una permutación.

Espacio Auxiliar: O(|s|)